|
Неоднократно находил ошибки в тестах, особенно в экзаменационных вопросах, когда правильно данный ответ на вопрос определялся в итоге как не правильно отвеченный... Из-за этого сильно страдает конечный бал! Да еще в заблуждение студентов вводит! Они-то думают, что это они виноваты!!! Но они тут не причем! Я много раз проверял ответы на некоторые такие "ошибочные" вопросы по нескольким источникам - результат везде одинаковый! Но ИНТУИТ выдавал ошибку... Как это понимать? Из-за подобных недоразумений приходиться часами перерешивать экзамен на отличную оценку...!!! Исправьте, пожалуйста, такие "ошибки"... |
Системы представления знаний
Исчисления предикатов
Традиционная булева алгебра и исчисление высказываний [ 2.3 ] не всегда подходят для выражения логических рассуждений, проводимых людьми, более удобен для этого язык логики предикатов. Под исчислением предикатов понимается формальный язык для представления отношений в некоторой предметной области. Исчисление предикатов подробно обсуждается в ряде книг по теории ИИ [ 1.1 ] , [ 1.6 ] , [ 2.3 ] . Основное преимущество исчисления предикатов - хорошо понятный мощный механизм математического вывода, который может быть непосредственно запрограммирован. Дальнейшее изложение ведется с учетом того, что читатель знаком с основами булевой алгебры.
Предикатом называют предложение, принимающее только два значения: "истина" или
"ложь". Для обозначения предикатов применяются
логические связки между высказываниями: 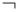 - не,
- не, 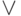 - или,
- или, 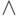 - и,
- и,  - если, а также квантор
- если, а также квантор  существования и квантор всеобщности
существования и квантор всеобщности 
 - существует такой x, что ...
- существует такой x, что ...
 - для любого x
- для любого x
Таким образом, логика предикатов оперирует логическими связками между высказываниями, например, она решает вопросы: можно ли на основе высказывания A получить высказывание B и т.д.
Рассмотрим некоторые примеры. Высказывание "у каждого человека есть отец" можно записать:
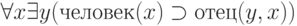
Выражение "Джон владеет красной машиной" записывается, например, так:

Рассмотрим вывод, дающий заключение на основе двух предпосылок:
Предпосылка 1: Все люди смертны
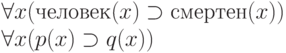
Предпосылка 2: Сократ - человек
p(a)
Заключение: Сократ - смертен
Смертен(Сократ) q(a)
Если обозначить через f функцию одного аргумента, то логическая формула для этого высказывания будет иметь вид:
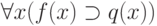
Алфавит логики предикатов состоит из элементов (символов):
x, y, z, u, v, w - переменные;
f, g, h - функциональные символы;
p, q, r, s, t - предикатные символы;
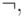
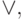
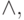


 - логические символы.
- логические символы.
Запишем на языке исчисления предикатов некоторое выражение:
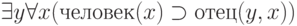
Что означает записанное выражение? Ответ очевиден: "у всех людей общий отец".
Приведем пример простого доказательства на языке исчисления предикатов.
Даны следующие факты:
- "Иван является отцом Михаила" - отец(a,b)
- "Петр является отцом Василия" - отец(c,d)
- "Иван и Петр являются братьями" -

Даны следующие определения:
- "Брат отца является дядей" -

- "Сын дяди является двоюродным братом" -

Требуется доказать, что "Михаил и Василий являются двоюродными братьями":

Делаем подстановки y = Иван, b = Михаил и x = Петр, d = Василий, видим, что предикаты 1, 2, 3 дают правильное предложение 6.
Рассмотренный нами язык называется исчислением предикатов первого порядка и позволяет связывать знаком квантора переменные, соответствующие объектам из предметной области, но не предикаты или функции.
Исчисление предикатов второго порядка позволяет связывать знаком квантора не только переменные, соответствующие объектам из предметной области, но и предикаты или функции. Примером исчисления предикатов второго порядка может служить выражение "Единственное качество Джона - это честность", которое записывается так:

На этом мы закончим знакомство с этой моделью и вернемся к ней в следующей лекции при рассмотрении правил вывода, принципа резолюции и методов поиска на основе исчисления предикатов.
