Решение обыкновенных дифференциальных уравнений и систем

9.5 Функции для решения дифференциальных уравнений

Наиболее часто используемыми в Octave функциями для решения дифференциальных уравнений являются:

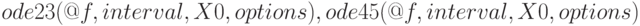• — функции решений обыкновенных нежёстких дифференциальных уравнений (или систем) методом Рунге-Кутта 2-3-го и 4-5-го порядка точности соответственно;
• —функции решений обыкновенных жёстких дифференциальных уравнений (или систем).

Функции решают систему дифференциальных уравнений автоматически подбирая шаг для достижения необходимой точности. Входными параметрами этих функций являются:

• — вектор-функция для вычисления правой части дифференциального уравнения или системы^{1При обращении к функциям odeXX используется указатель @f на функцию. (Прим. редактора).};
• — массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы;
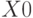• — вектор начальных условий системы дифференциальных систем;
• — параметры управления ходом решения дифференциального уравнения или системы.

Для определения параметров управления ходом решения дифференциальных уравнений используется функция odeset следующей структуры:

Здесь

• — имя i-го параметра;
• — значение i-го параметра.

При решении дифференциальных уравнений необходимо определить следующие параметры:

• — относительная точность решения, значение по умолчанию ;
• — абсолютная точность решения, значение по умолчанию ;
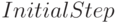• — начальное значение шага изменения независимой переменной, значение по умолчанию 0.025;
• — максимальное значение шага изменения независимой переменной, значение по умолчанию 0.025.

Все функции возвращают:

• массив — координат узлов сетки, в которых ищется решение;
• матрицу -й столбец которой является значением вектор-функции решения в узле .

Решим задачу 9.1 с использованием функций 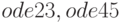. Текст программы с комментариями представлен в листинге 9.8.

	
% Точное решение системы.
function q= fi(x)
	q=119/296-exp(6*x)+1/24*(52*x.^3+114*x.^2-30*x+39)-6*sin(x
		)/37-cos(x)/37;
end
% Правая часть дифференциального уравнения.
function y=g(t, x)
	y=6*x-13*t^3-22*t^2+17*t-11+sin(t);
end
% Определение параметров управления ходом решения уравнения.
% RelTol — относительная точность решения 1E-5,
% AbsTol — абсолютная точность решения 1E-5,
% InitialStep — начальное значение шага изменения переменной 0.025,
% MaxStep — максимальное значение шага изменения переменной 0.1.
par=odeset("RelTol", 1e-5, "AbsTol", 1e-5, ’InitialStep’
	, 0.025, ’MaxStep’, 0.1);
% Решение дифференциального уравнения методом Рунге-Кутта 2–3 порядка.
[X23, Y23]= ode23 (@g, [0 0.25], 2, par);
% Определение параметров управления ходом решения уравнения.
% RelTol — относительная точность решения 1E-4,
% AbsTol — абсолютная точность решения 1E-4,
% InitialStep — начальное значение шага изменения переменной 0.005,
% MaxStep — максимальное значение шага изменения переменной 0.2.
par=odeset("RelTol", 1e-4, "AbsTol",1e-4, ’InitialStep’, 0.05, ’
	MaxStep’, 0.2);
% Решение дифференциального уравнения методом Рунге-Кутта 4–5 порядка.
[X45, Y45]=ode45(@g, [0 0.25], 2, par);
% Точное решение
x1 = 0:0.05:0.25;
y1= fi(x1);
% График решения функцией ode23 и точного решения.
plot(x1, y1, ’-g;exact solution;’, X23, Y23, ’*b;ode23;’);
grid on;
figure();
% График решения функцией ode45 и точного решения.
plot(x1, y1, ’-g;exact solution;’, X45, Y45, ’*b;ode45;’);
grid on;

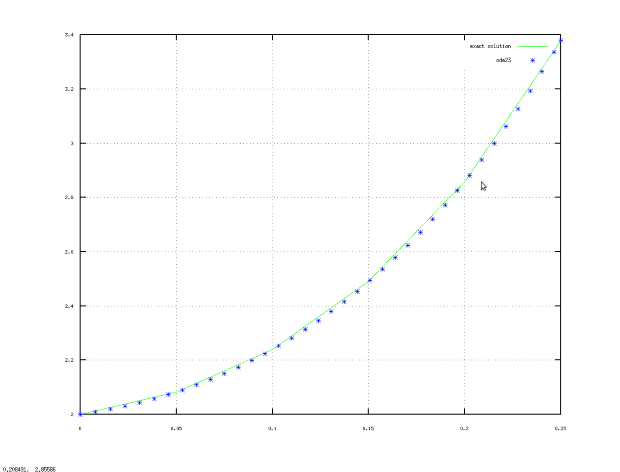
На рис. 9.5 представлено решение, найденное с помощью функции с точностью 1E-5 и точное решение. На рис. 9.6 представлено решение, найденное с помощью функции с точностью 1E-4 и точное решение.

Функции и позволяют найти решение с заданной точностью, однако, как и следовало ожидать, при использовании метода Рунге-Кутта более высокой точности шаг изменения переменной намного меньше.

Рассмотрим пример решения жёсткой системы дифференциальных уравнений. Напомним читателю определение жёсткой системы дифференциальных уравнений. Система дифференциальных уравнений -го порядка

( 9.28)

называется жёсткой [2], если выполнены следующие условия:

• ействительные части всех собственных чисел матрицы B(n) отрицательны
• величина
  
  , называемая числом жёсткости системы, велика. При исследовании на жёсткость нелинейной системы дифференциальных уравнений (9.27) в роли матрицы B будет выступать матрица частных производных.

увеличить изображение
Рис. 9.5. Графики точного решения задачи 9.1 и решения, найденного с помощью функции ode23

увеличить изображение
Рис. 9.6. Графики точного решения задачи 9.1 и решения, найденного с помощью функции ode45

Пример 9.2. Решить задачу Коши для жёсткой системы дифференциальных уравнений:

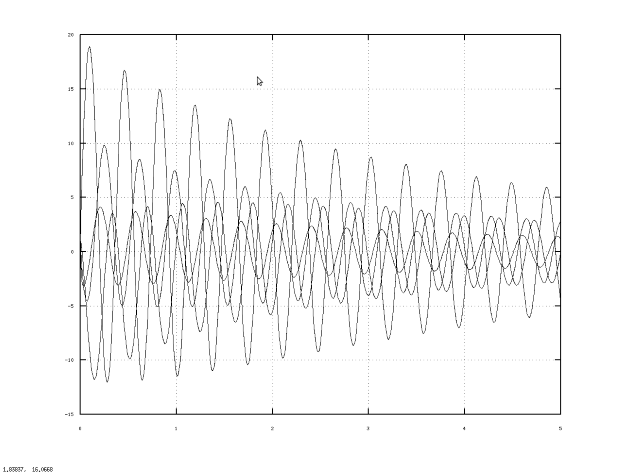
Решение задачи с комментариями представлено в листинге 9.9, на рис. 9.7 можно увидеть график решения.

	
% Функция правой части жёсткой системы дифференциальных уравнений.
function dx=syst1(t, x)
	B=[119.46 185.38 126.88 121.03; -10.395 -10.136 -3.636 8.577;
		–53.302 –85.932 –63.182 –54.211;–115.58 –181.75 –112.8 –199];
	dx=B-x;
end
% Определение параметров управления ходом решения жёсткой
% системы дифференциальных уравнений.
% RelTol — относительная точность решения 1E-8,
% AbsTol — абсолютная точность решения 1E-8,
% InitialStep — начальное значение шага изменения переменной 0.02,
% MaxStep — максимальное значение шага изменения переменной 0.1.
par=odeset("RelTol",1e-8, "AbsTol",1e-8, ’InitialStep’, 0.02, ’
	MaxStep’, 0.1);
% Решение жёсткой системы дифференциальных уравнений.
[ A,B]= ode2r(@syst1, [0 5], [1; 1; 1; 1], par);
% Построение графика решения.
plot(A, B, ’-k’); grid on;

Этим примером мы заканчиваем краткое описание возможностей Octave для решения дифференциальных уравнений. Однако, следует помнить о следующем: решение реального дифференциального уравнения (а тем более системы) — достаточно сложная математическая задача. Для её решения недостаточно знания синтаксиса функций Octave, необходимо достаточно глубоко знать математические методы решения подобных задач. При решении дифференциальных уравнений необходимо определить метод решения и только потом пытаться использовать встроенные функции или писать свои. Авторы не случайно достаточно подробно напомнили читателю основные численные методы решения дифференциальных уравнений и систем. На наш взгляд без знания численных и аналитических методов решения дифференциальных уравнений, достаточно проблематично решить реальную задачу.

увеличить изображение
Рис. 9.7. График решения задачи 9.2

Кроме того, следует помнить, что функциями 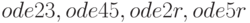возможности пакета не ограничиваются. Octave предоставляет достаточное количество функций для решения дифференциальных уравнений различного вида. Они подробно описаны в справке консольной версии приложения^{2Ещё раз напоминаем читателю, что справка по Octave, доступная из оболочки qtoctave недостаточно полная.}.

Множество функций для решения дифференциальных уравнений находится в пакете расширений odepkg. Краткое описание функций этого пакета на английском языке с некоторыми примерами приведено на странице http://octave.sourceforge.net/odepkg/overview.html.