НОУ ИНТУИТ | Введение в Octave. Лекция 6: Векторная алгебра и аналитическая геометрия

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 12.03.2015 | Доступ: свободный | Студентов: 576 / 64 | Длительность: 20:55:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 14 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

6.2 Аналитическая геометрия

Плоскость, проходящая через точку 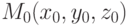$M_{0}(x_{0}, y_{0}, z_{0})$ и перпендикулярная к вектору $\vec{N}\{A,B,C\}$ представляется уравнением $A(x-x_{0})+B(y-y_{0})+C(z-z_{0})=0$ или Ax+By+Cz+D=0 .

Вектор $\vec{N}\{A,B,C\}$ называется нормальным вектором плоскости.

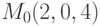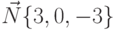Пример 6.13. Записать уравнение и построить плоскость, проходящую через точку M_0 (2, 0, 4) и перпендикулярную вектору $\vec{N}\{3,0,-3\}$ .

Исходя из условия примера уравнение плоскости имеет вид $3(x-2)+0(y-1)-3(z-4)=0\Rightarrow 3x-6-3z+12=0\Rightarrow 3x-3z+6=0$ .

Для построения плоскости средствами Octave преобразуем уравнение плоскости к виду функции двух переменных:

$Ax+By+Cz+D=0\Rightarrow z(x,y)=-{\frac{A}{C}}x-\frac{B}{C}y-\frac{D}{C},\\ z(x,y)=b_{0}+b_{1}x+b_{2}y,b_{0}=-{\frac{A}{C}},b_{1}=\frac{-{B}}{C},b_{2}=\frac{-{D}}{C}.$

Рис. 6.10. Изображение плоскости и её направляющего вектора

Решение примера представлено в листинге 6.13 и на рис. 6.10

	
clf; cla;
set(gcf, ’Position’, [ 20, 20, 400, 400 ] );
axis ( [ 0, 1 0, 0, 1 0, 0, 1 0 ] )
A=3;B=0;C=_3;D=6;N=[A, B,C ]; % Параметры плоскости
b0= - D/C; b1= - A/C; b2= - B/C; % Параметры уравнения плоскости, преобразо% ванного к функции двух переменных
								% Построение плоскости
xk=5;yk=5;
X= 0 : 0.5 : xk;Y= 0 : 0.5 : yk;
[ x, y]= meshgrid(X,Y);
z=b0+b1*x+b2 * y;
surf( x, y, z ), colormap gray
grid on; xlabel ( ’x’, ’FontSize’, 2 0 );
ylabel( ’y’, ’FontSize’, 2 0 ); zlabel( ’z’, ’FontSize’, 2 0 );
set( gca, ’FontSize’, 1 2 ); set ( gca, ’box’, ’on’ );
% Построение направляющего вектора
line( [ xk, 0 ], [ 0, 0 ], [ b0, yk+b0 ], ’LineWidth’, 5, ’Color’, ’k’ );
line( [ 0, 0 ], [ 0, 0 ], [ yk+b0, yk+b0 ], ’LineWidth’, 5, ’Color’, ’k’, ’
	marker’, ’v’, ’markersize’, 1 6 );
text(0+0.3,0+0.3, yk+b0 _1, ’N’, ’FontSize’, 2 0 );
title( ’3x-3z+6=0’, ’FontSize’, 2 0 ) % Заголовок

Листинг 6.13. Построение плоскости по точке и вектору (пример 6.13).

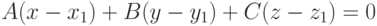Если плоскость проходит через заданную точку $M_{1}(x_{1,}y_{1,}z_{1})$ и параллельна плоскости Ax + By + Cz + D = 0 , то её уравнение записывают так $A(x-x_{1})+B(y-y_{1})+C(z-z_{1})=0$ .

Рис. 6.11. Параллельные плоскости

Пример 6.14. Записать уравнение и построить плоскость, проходящую через точку 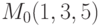M_0 (1, 3, 5) параллельно плоскости 3x - 3z + 6 = 0 .

Уравнение плоскости имеет вид: $3(x-1)-3(z-5)=0\Rightarrow 3x-3-3z+15=0\Rightarrow 3x-3z+12=0$ .

Решение примера показано на рис. 6.11 и в листинге 6.14.

	
function p=plos(A, B, C,D)
	% Параметры уравнения плоскости, преобразованного
	b0= - D/C; b1= - A/C; b2= - B/C; % к функции двух переменных
	% Построение плоскости
	xk=5;yk=5;
	X= 0 : 0.5 : xk;Y= 0 : 0.5 : yk;
	[ x, y]= meshgrid(X,Y);
	z=b0+b1 * x+b2 * y;
	surf( x, y, z ), colormap gray
	grid on;
	p=0;
end;
clf; cla; set( gcf, ’Position’, [ 20, 20, 400, 400 ] );
axis( [ 0, 10, 0, 10, 0, 10 ] )
A1=3;B1=0;C1=_3;D1=6; % Параметры плоскости
% Построение плоскостей
plos(A1, B1, C1, D1)
hold on
A2=3;B2=0;C2=_3;D2=12;
p=plos(A2, B2, C2, D2)
xlabel( ’x’, ’FontSize’, 2 0 ); ylabel( ’y’, ’FontSize’, 2 0 );
zlabel( ’z’, ’FontSize’, 2 0 );
set( gca, ’FontSize’, 1 2 ); set( gca, ’box’, ’on’ );
M= [ 1, 3, 5 ]; % Изображение точки
line( [M( 1 ),M( 1 ) ], [M( 2 ),M( 2 ) ], [M( 3 ),M( 3 ) ], ’LineWidth’, 5, ’Color’
	, ’k’, ’marker’, ’o’, ’markersize’, 1 6 );
text(M( 1 ) _0.5,M( 2 ) +0.5,M( 3 ) +1, ’M(1,3,5)’, ’FontSize’, 2 0 );
title( ’3x-3z+6=0,3x-3z+12=0’, ’FontSize’, 2 0 )

Листинг 6.14. Построение плоскости по параллельной ей плоскости и точке (пример 6.14).

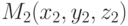Если три точки $M_{0}(x_{0}, y_{0}, z_{0}),M_{1}(x_{1}, y_{1}, z_{1})$ и $M_{2}(x_{2}, y_{2}, z_{2})$ не лежат на одной прямой, то уравнение плоскости, проходящей через них, представляется уравнением:

$\left\arrowvert\begin{matrix}x-x_{0}&y-y_{0}&z-z_{0}\\x_{1}-x_{0}&y_{1}-y_{0}&z_{1}-z_{0}\\x_{2}-x_{0}&y_{2}-y_{0}&z_{2}-z_{0}\end{matrix}\right\arrowvert=0.$

Пример 6.15. Записать уравнение и построить плоскость, проходящую через точки M_0(1, 2, 3), M_1(2, 1, 2) и M_2(3, 3, 1) .

Заданные точки не лежат на одной прямой, так как векторы $\overrightarrow{{M_{0}M_{1}}}$ и $\overrightarrow{{M_{0}M_{2}}}$ не коллинеарны. ли. 6.12 и рис. 6.13 иллюстрируют это утверждение. Изображение на рис. 6.12 получено в результате работы программы показанной в листинге 6.15. Рис. 6.13 получен из ррис. 6.12ис путём поворота^{2Аналитически поворот можно осуществить с помощью функции view, например, view(37.5,30); вернуть рисунок в исходное состояние можно командой view(2) (прим. редактора ).} в графическом окне.

	
clf; cla;
set( gcf, ’Position’, [ 20, 20, 400, 400 ] );
set( gca, ’Position’, [ . 1, . 1, . 8, . 8 ] );
set( gca, ’xlim’,[0,3]); set ( gca, ’ylim’,[0,3]); set ( gca, ’zlim’,[0,3]);
set( gca, ’xtick’,[0:3]); set ( gca, ’ytick’,[0:3]); set ( gca, ’ztick’,[0:3]);
set( gca, ’box’, ’on’ ); xlabel ( ’x’ ); ylabel ( ’y’ ); zlabel ( ’z’ );
axis( [ 0, 3, 0, 3, 0, 3 ] )
grid on;
M0= [ 1, 2, 3 ];M1= [ 2, 1, 2 ];M2= [ 3, 3, 1 ]; % Исходные данные
% Изображение векторов M0M1 и M0M2
line ([M1(1),M0(1)],[M1(2),M0(2)],[M1(3),M0(3)],’LineWidth’,5,’Color’,’k’);
line ([M2(1),M0(1)],[M2(2),M0(2)],[M2(3),M0(3)],’LineWidth’,5,’Color’,’k’);
% Изображение стрелок на векторах
line ([M1(1),M1(1)],[M1(2),M1(2)],[M1(3),M1(3)], ’LineWidth’, 5, ’Color’, ’k
	’, ’marker’, ’>’, ’markersize’, 10 );		
line ([M2(1),M2(1)],[M2(2),M2(2)],[M2(3),M2(3)], ’LineWidth’, 5, ’Color’, ’k
	’, ’marker’, ’<’, ’markersize’, 10 );
line ([M0(1),M0(1)],[M0(2),M0(2)],[M0(3),M0(3)], ’LineWidth’, 5, ’Color’, ’k
	’, ’marker’, ’o’, ’markersize’, 10 );
% Подписи
text(M0( 1 ),M0( 2 ) +0.3,M0( 3 ), ’M0’, ’FontSize’, 2 0 );
text(M1( 1 ),M1( 2 ) +0.3,M1( 3 ), ’M1’, ’FontSize’, 2 0 );
text(M2( 1 ),M2( 2 ) +0.3,M2( 3 ), ’M2’, ’FontSize’, 2 0 );

Листинг 6.15. Построение векторов по трём точкам (пример 6.15).

Рис. 6.12. Иллюстрация к примеру 6.15 (векторы на плоскости)

Рис. 6.13. Иллюстрация примеру 6.15 (векторы в пространстве)

Рис. 6.14. Плоскость, проходящая через три точки

Плоскость представлена уравнением:

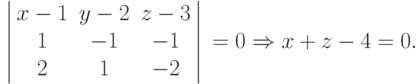
$\left\arrowvert\begin{matrix}x-1&y-2&z-3\\1&-1&-1\\2&1&-2\end{matrix}\right\arrowvert =0\Rightarrow x+z-4=0.$

Графическое изображение плоскости показано на рис. 6.14. Текст программы в листинге 6.16.

	
clf; cla;
set ( gcf, ’Position’, [ 20, 20, 400, 400] ); axis ( [ 0, 10, 0, 10, 0, 10 ] )
A=1;B=0;C=1;D=-4;N=[A, B,C ]; % Параметры плоскости
% Параметры уравнения плоскости, преобразованного
% к функции двух переменных
b0= - D/C; b1= - A/C; b2= - B/C;
% Построение плоскости
xk=3;yk=3;X= 0 : 0.5 : xk;Y= 0 : 0.5 : yk;
[ x, y]= meshgrid(X,Y);
z=b0+b1*x+b2 * y;
surf ( x, y, z ), colormap gray
grid on;
xlabel ( ’x’, ’FontSize’, 20 ); ylabel ( ’y’, ’FontSize’, 20 );
zlabel ( ’z’, ’FontSize’, 20 );
set ( gca, ’FontSize’, 12 ); set ( gca, ’box’, ’on’ );
% Построение направляющего вектора
line ( [ xk, 0 ], [ 0, 0 ], [ b0, b0_yk ], ’LineWidth’, 5, ’Color’, ’k’ );
line ( [ xk, xk ], [ 0, 0 ], [ b0, b0 ], ’LineWidth’, 5, ’Color’, ’k’, ’marker’,
	’v’, ’markersize’, 16 );
text (0+0.3,0+0.3, b0-yk, ’N’, ’FontSize’, 20 );
% Исходные данные
M0= [ 1, 2, 3 ];M1= [ 2, 1, 2 ];M2= [ 3, 3, 1 ];
% Нанесение точек на график
line ( [M1( 1 ),M1( 1 ) ], [ M1( 2 ),M1( 2 ) ], [ M1( 3 ),M1( 3 ) ], ’LineWidth’, 5, ’
	Color’, ’k’, ’marker’, ’o’, ’markersize’, 10 );
line ( [M2( 1 ),M2( 1 ) ], [ M2( 2 ),M2( 2 ) ], [ M2( 3 ),M2( 3 ) ], ’LineWidth’, 5, ’
	Color’, ’k’, ’marker’, ’o’, ’markersize’, 10 );
line ( [M0( 1 ),M0( 1 ) ], [ M0( 2 ),M0( 2 ) ], [ M0( 3 ),M0( 3 ) ], ’LineWidth’, 5, ’
	Color’, ’k’, ’marker’, ’o’, ’markersize’, 10 );
% Подписи
text (M0( 1 ) -0.3,M0( 2 ) -0.3,M0( 3 ), ’M0’, ’FontSize’, 20 );
text (M1( 1 ) -0.3,M1( 2 ) -0.3,M1( 3 ), ’M1’, ’FontSize’, 20 );
text (M2( 1 ) -0.3,M2( 2 ) -0.3,M2( 3 ), ’M2’, ’FontSize’, 20 );
% Заголовок
title ( ’x+z-4=0’, ’FontSize’, 20 )

Листинг 6.16. Построение плоскости по трём точкам (Пример 6.15).

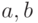Если плоскость Ax + By + Cz + D = 0 не параллельна оси OX $(A\neq 0)$ , то она отсекает на этой оси отрезок $a=-{\frac{D}{A}}$ . Аналогично отрезки на осях OY, OZ будут $b=-{\frac{D}{B}},(B\neq 0)$ и $\text{с}=-{\frac{D}{C}},(C\neq 0)$ . Таким образом, плоскость отсекающую на осях отрезки a, b и можно представить уравнением

$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1,$

которое называется уравнением плоскости в отрезках.

Пример 6.16. Написать уравнение плоскости 3x - 6y +2z - 12 = 0 в отрезках и построить эту плоскость.

Найдём длины отрезков: 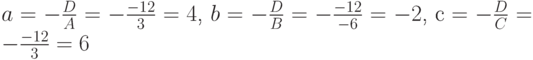$a=-{\frac{D}{A}}=-{\frac{-12}{3}}=4$, $b=-{\frac{D}{B}}=-{\frac{-12}{-6}}=-2$, $\text{с}=-{\frac{D}{C}}=-{\frac{-12}{3}}=6$ .

Запишем уравнение плоскости в отрезках:

$\frac{x}{4}+\frac{y}{-2}+\frac{z}{6}=1.$

Решение примера показано на рис. 6.15 и в листинге 6.17.

	
clf; cla;
a =4;b=_2;c =6;
set( gcf, ’Position’, [ 50, 50, 400, 400 ] );
axis ( [ 0, a, 0, b, 0, c ] );
X= 0 : 0.2 : a;Y=b : 0.2 : 0;
[ x y]= meshgrid(X,Y);	
z=c-c /a * x-c /b * y;
hfig=surf ( x, y, z );
set( hfig, ’FaceColor’, ’none’, ’EdgeColor’, ’k’ )
% Изображение векторов a, b и c
line( [ 0, a ], [ 0, 0 ], [ 0, 0 ], ’LineWidth’, 5, ’Color’, ’k’ );
line( [ 0, 0 ], [ 0, b ], [ 0, 0 ], ’LineWidth’, 5, ’Color’, ’k’ );
line( [ 0, 0 ], [ 0, 0 ], [ 0, c ], ’LineWidth’, 5, ’Color’, ’k’ );
% Подписи
text( a / 2, 0, 1, ’a’, ’FontSize’, 20 );
text( 0, b / 2, 1, ’b’, ’FontSize’, 20 );
text( 0.2, 0, c /2, ’c’, ’FontSize’, 20 );
% Заголовок
title( ’a=4, b=-2, c=6’, ’FontSize’, 14 )
xlabel( ’x’ ); ylabel ( ’y’ ); zlabel ( ’z’ );
set( gca, ’Position’, [ .1, .1, .8, .8 ] );
set( gca, ’View’, [ 25 22 ] )

Листинг 6.17. Уравнение плоскости в отрезках (пример 6.16).

Рис. 6.15. Плоскость, заданная отрезками

Дальше >>

Авторизоваться

Введение в Octave

Векторная алгебра и аналитическая геометрия

6.2 Аналитическая геометрия

Вопросы и ответы