Общая теория систем
3.3 Состав и структура общей теории систем.
Проведенный анализ современного состояния общей теории систем, ее области и задач исследования, а также результаты исследования систем (глава 1), системного анализа (глава 2) и возможностей метанаук (философии и математики, глава 3) позволяют следующим образом определить состав и структуру ОТС.
Будем считать, что ОТС — это дедуктивная аксиоматическая теория, состоящая из двух частей: неформальной, или ОТС1 (рис. 14, 16, уровень "5" "Содержания" в ромбовидной и пирамидальной структурах системного анализа), и формальной, или ОТС2 (рис. 14, 16, уровень "-5" "Формы").
ОТС1 включает в себя: общие понятия системного анализа; аксиомы — гипотезы и аксиоматизированные отношения между понятиями; правила вывода — категориальные структуры, законы диалектики, дедуктивная диалектическая логика (табл. 8).
За основу ОТС2 мы принимаем теорию L исчисления высказываний: алфавит ОТС2 — это алфавит L, ограниченный понятиями ОТС1; аксиомы ОТС2 — это аксиомы L, дополненные аксиомами ОТС1, удовлетворяющие требованиям теорем в L (чтобы теория L не превратилась в противоречивую теорию); правила вывода ОТС2 — это правило вывода теории L, или MP (табл. 8).
У ОТС1 область допустимых и область истинностных высказываний шире, чем у ОТС2, но границы областей и сама истинность менее четкая, чем у ОТС2. Поэтому эти две части теории естественным образом дополняют друг друга.
МЕТОДИЧЕСКИЕ ПОЯСНЕНИЯ. Теперь необходимо решить две задачи: 1) доказать, что новые аксиомы ОТС2 являются теоремами теории L и, следовательно, ОТС2 — непротиворечива; 2) вывести теоремы о внутренней и внешней структурах функции системы и их эквивалентности — это позволит перейти к исследованию классов и типов систем, а структуру функции использовать для исследования стадий существования системы.
Теорема 1. Доказать в теории L  .
.
По определению, эквивалентность означает: а)  и б)
и б)  .
.
а)  ,
,
- N посылка,
- R посылка,
-
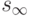 посылка,
посылка, -
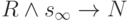 по определению,
по определению, -
 по определению,
по определению, -
 по определению,
по определению, - rG MP(2,5),
 |
- sN MP(3,6),
-
 преобразование тавтологии,
преобразование тавтологии, -
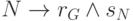 от противного, с точностью до изоморфизма.
от противного, с точностью до изоморфизма.
б)  ,
,
- sN посылка,
- rG посылка,
- R посылка,
-
 посылка,
посылка, -
 по определению,
по определению, -
 по определению,
по определению, -
 по определению,
по определению, -
 от противного, с точностью до изоморфизма.
от противного, с точностью до изоморфизма.
Теорема 2. Доказать в теории L  . Покажем, что правая часть определения F не противоречит аксиомам L: АС1 — при определении по индукции; АС2 — при определении по индукции для ti, ti+1, ti+2; АС3-АС13 — доказывается подстановкой.
. Покажем, что правая часть определения F не противоречит аксиомам L: АС1 — при определении по индукции; АС2 — при определении по индукции для ti, ti+1, ti+2; АС3-АС13 — доказывается подстановкой.
Теорема 3. Доказать в теории L  . Правая часть определения не противоречит аксиомам L при доопределении в L:
. Правая часть определения не противоречит аксиомам L при доопределении в L:  .
.
Теорема 4. Доказать в теории L  . Правая часть определения не противоречит аксиомам L при использовании трех аксиомных схем. AC1:
. Правая часть определения не противоречит аксиомам L при использовании трех аксиомных схем. AC1: 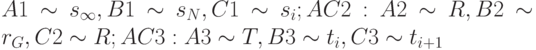 .
.
Теорема 5. Доказать в теории L 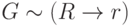 . Правая часть определения не противоречит аксиомам L, если ввести дополнительную схему аксиом. AC:
. Правая часть определения не противоречит аксиомам L, если ввести дополнительную схему аксиом. AC: 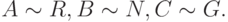
В определение функции системы (теорема 2) заложено воспроизводство внутренних свойств, определяемое стационарностью и устойчивостью системы во времени, т. е. F здесь выражена через внутреннюю функциональную структуру.
Внешнюю структуру F, или структуру внешних отношений системы, мы определим из условия выделения системы во внешней среды и в объекте-носителе во времени:
 .
.
Подставим значения S, B, V по определению (из табл. 8), получим КНФ:
 (3.2).
(3.2).
Подставим в левую часть значение F, выраженное через внутренние характеристики:


Исключив импликацию, получим КНФ, которую преобразуем в следующую ДНФ:
 (3.3).
(3.3).
Таким образом, мы получили в ДНФ и КНФ структуру <S, B, V, T>, порождающую функцию системы.
