Биткоин и технологии криптовалюты

Цифровые подписи

Цифровая подпись представляет собой второй криптографический примитив вместе с хэш-функциями, которые нужны в качестве составных блоков для последующего разговора о криптовалюте. Цифровая подпись должна быть похожа на подпись на бумаге, только в цифровой форме.

Требования к подписям:

• Подписать может только один человек, но все могут проверить. Точно так же, как с подписью на бумаге.
• Подпись связана с определенным документом, ее нельзя вырезать и вставить в другой документ. Потому что подпись не просто подпись, она означает согласие или одобрение конкретного документа.

Вопрос в том, как это можно реализовать в цифровой форме с использованием криптографии?

Рис. 1.12. API цифровых подписей

API для цифровых подписей показан на рис. 1.12.

Есть три операции, которые необходимо сделать. Первая – генерация ключей с помощью операции generateKeys. Входным параметром служит значение размера ключа (keysize) в битах. Эта процедура генерирует два ключа — sk и pk. sk — закрытый, секретный ключ подписи. Это информация, которую необходимо держать в секрете и использовать для создания своей подписи. А pk - это открытый, общедоступный ключ проверки, который можно дать любому, чтобы он мог проверить достоверность подписи.

Вторая операция — это операция подписи. Здесь используется закрытый ключ подписи и сообщение, на котором необходимо поставить подпись. Это действие возвращает sig (комбинацию битов), которая является подписью. И затем, третья операция — это проверка, которая берет то, что считается истинной подписью и проверяет ее достоверность. Для ее выполнения берется открытый ключ подписывающего лица, подписанное сообщение и подпись. Эта операция отвечает на вопрос, настоящая ли это подпись, возвращая значение "да" или "нет".

Итак, эти три операции составляют схему подписи. Необходимо отметить, что первые две операции могут использовать рандомизированные алгоритмы. generateKeys должно быть рандомизированным, потому что эта операция должна генерировать разные ключи для разных людей.

Требования к подписям:

1. "достоверные подписи подтверждаются": verify(pk, message, sign(sk,message)) == true
2. "подпись нельзя подделать": злоумышленник, знающий pk и имеющий возможность видеть подписи на любых сообщениях, не может создать проверяемую подпись на другом сообщении.

Первое требование - валидная подпись подтверждается. Это значит, что если подпись поставлена человеком A с использованием закрытого ключа A, другой человек B с использованием открытого ключа A может проверить эту подпись, и она будет корректна. Второе требование состоит в том, что подпись невозможно подделать. То есть злоумышленник, который знает чей-то открытый ключ (ключ для верификации) и видит подписи на других сообщениях, не может подделать подпись на каком-то конкретном сообщении.

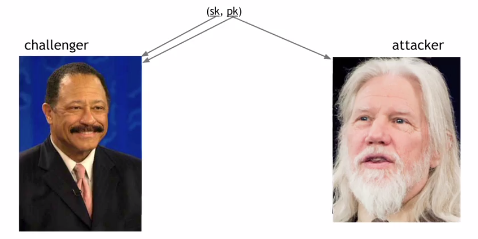
Это свойство обычно объясняют с помощью импровизированной игры со злоумышленником ( рис. 1.13).

Рис. 1.13. Игра со злоумышленником

На рис. 1.13 слева находится бросающий вызов телевизионный судья, который собирается проверить заявление взломщика. Взломщик утверждает, что он может подделывать подписи. Необходимо проверить это заявление. Первое, что нужно сделать, - с помощью функции generateKeys сгенерировать закрытый и открытый ключи, которые соответствуют друг другу. Закрытый ключ остается у судьи, открытый предоставляется и судье и взломщику ( рис. 1.14).

Рис. 1.14. Генерация ключей

Таким образом, взломщик знает только открытый ключ. И его задача — попытаться подделать сообщение. Судья знает секретный ключ, поэтому он может ставить подписи.

Если говорить о применении к реальности, то реальный злоумышленник может видеть настоящие подписи своей возможной жертвы на ряде различных документов. И даже, возможно, что злоумышленник может заставить жертву подписать нужный ему документ, ни чем не отличающийся от обычных, если это ему необходимо. Поэтому здесь тоже сделано допущение, что взломщик может получать подписи на ряде нужных ему документов.

Рис. 1.15. Злоумышленник отправляет судье сообщение

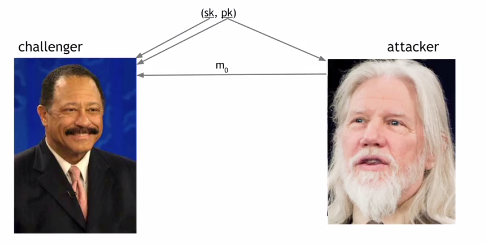
Взломщик собирается отправить сообщение (m0) судье ( рис. 1.15). Судья подписывает это сообщение и отправляет подписанное обратно. Взломщик может посмотреть на это, почесать голову, и отправить другое сообщение (m1).

Рис. 1.16. Получение злоумышленником подписанных сообщений от судьи

Судья подпишет и его ( рис. 1.16). Взломщик может отправить любое количество сообщений и получить на них подписи.

Как только взломщик удостоверится, что увидел достаточно подписей, он выберет сообщение m, на котором хочет подделать подпись, и попытается это сделать ( рис. 1.17).

Рис. 1.17. Подделка подписи под сообщением

И, конечно, есть правило, что сообщение m, на котором он пытается подделать подпись, не из тех сообщений, которое он уже видел. Потому что ему будет несложно отправить действительную подпись на сообщении m0, потому что судья отправил действительную подпись на m0 раньше. Поэтому он выбирает другое сообщение, на котором не видел подпись.

После получения бросающий вызов запустит алгоритм проверки, с помощью открытого ключа ( рис. 1.18).

Рис. 1.18. Проверка подписи, которую подделал злоумышленник

И если алгоритм возвращает значение true, то взломщик победил, так как он смог подделать подпись.

Необходимо отметить, что вероятность выигрыша у взломщика ничтожно мала. Цифровая подпись не может быть подделана, если у взломщика есть ничтожно малый шанс подделать сообщение, вне зависимости от используемого им алгоритма. Если говорить о практических аспектах применения цифровой подписи, необходимо отметить, что рассматриваемые алгоритмы рандомизированы (по крайней мере, некоторые из них). Поэтому для их реализации необходим хороший источник случайности. Недостаточная степень случайности сделает алгоритм небезопасным. Также на практике есть ограничение на размер сообщения, которое можно подписать, потому что реальные схемы будут работать с битовыми строками ограниченной длины. Решением этой проблемы будет использование хэша сообщения, а не его всего. В этом случае сообщение может быть очень большим, а хэш содержать всего 256 бит.

А так как хэш-функции свободны от коллизий, то использовать хэш сообщения в качестве ввода в схему цифровой подписи безопасно. Помимо этого позже будет рассмотрено подписание хэш-указателя, который находится в конце цепочки блоков, то есть подпись всей цепочки блоков.

Биткоин использует определенную схему цифровой подписи, которая называется ECDSA. Это алгоритм цифровой подписи с эллиптической кривой, стандарт правительства США. В рамках данного курса не будут рассматриваться детали его работы, которые основываются на достаточно сложной математике. Заострим внимание только на том, что для ECDSA важна высокая степень случайности. При этом особенностью ECDSA является то, что даже если недостаточная степень случайности используется только в процессе подписи, а сам ключ совершенен, это всё равно приведет к его потере.

Терминологический словарь

Электронная подпись, цифровая подпись — реквизит электронного документа, полученный в результате криптографического преобразования информации с использованием закрытого ключа подписи и позволяющий проверить отсутствие искажения информации в электронном документе с момента формирования подписи (целостность), принадлежность подписи владельцу сертификата ключа подписи (авторство), а в случае успешной проверки подтвердить факт подписания электронного документа (неотказуемость).