Принцип отсутствия арбитражных возможностей
Облигации
Для финансирования своих инвестиций корпорации используют заемные, или долговые, средства. Наряду с банковским кредитованием распространённым способом получения заемных средств на открытом рынке являются облигации. Кроме корпораций эмитентами облигаций являются правительства государств (государственные облигации, government bonds) и муниципальные власти (муниципальные облигации, municipal bonds).
Облигация (bond) - долговое обязательство, выпускаемое заёмщиком (эмитентом), которое гарантирует кредитору (инвестору) выплату указанной суммы N через T лет и, чаще всего, периодическую выплату определённых процентов от этой суммы. Эти выплаты называются купонными платежами (coupon).
Денежная сумма N, указанная на облигации, которую заёмщик (эмитент) берет взаймы и обязуется выплатить по истечении определённого срока, называется её номинальной стоимостью (face value). Дата, на которую держатель облигации может получить номинальную стоимость облигации и после которой уже не осуществляется никаких платежей, называется датой погашения (maturity date). На практике выплата эмитентом номинальной стоимости облигации может выполняться в несколько этапов. Например, выплата номинальной стоимости N=1 000 руб. трёхгодичных муниципальных облигаций Ярославской области, выпущенных в июне 2008 г., происходила по следующей схеме: 15% от номинальной стоимости были выплачены с 4-ым купоном, по 10% - с 8-м и 9-м купонами, 65% - с последним, 12-м купоном2Эта и много другой полезной информации о российских облигациях имеется на сайтах www.rusbonds.ru и www.cbonds.info.
В рамках нашей лекции мы ограничимся рассмотрением классических типов облигаций, относящихся к инструментам с фиксированным доходом3В российской практике применяются и более сложные для анализа виды корпоративных облигаций, номинальная стоимость которых возвращается несколькими выплатами.
Купонные выплаты не являются постоянными, а определяются на аукционах в соответствии с проспектом эмиссии.}. В зависимости от того, в какой форме инвестору выплачивается доход, облигации делятся на купонные и бескупонные (последние также называются облигациями с нулевым купоном (zero-coupon bond)). Купонная облигация (coupon bond), как правило, продаётся в момент выпуска по номинальной цене N. В определённые сроки (p раз в год, p=1, 2 или 4) эмитент выплачивает инвестору доход в виде процентов от номинальной цены облигации (купонные платежи). Этот процент называется купонным доходом (coupon rate). По окончании срока T инвестору выплачивается доход по последнему купону и номинальная цена облигации.Когда-то, когда облигации выпускались в бумажном виде, к ним прилагались купоны, на которых указывались процент и даты его выплаты. В указанную даты владельцу облигации выплачивался причитающийся ему доход, а купон отрезался.
Обозначим через  величину i-го купонного платежа (
величину i-го купонного платежа ( ). Поток платежей по купонной облигации с выплатой купонного дохода два раза в год можно изобразить на оси времени следующим образом:
). Поток платежей по купонной облигации с выплатой купонного дохода два раза в год можно изобразить на оси времени следующим образом:
Если ставка процента по купону равна r, то купонный доход рассчитывается по формуле: 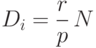 . Ещё раз обращаем внимание читателя на тот факт, что в финансах принято указывать годовые ставки процента, поэтому в двух предыдущих формулах годовая ставка процента делится на количество выплат в году (p).
. Ещё раз обращаем внимание читателя на тот факт, что в финансах принято указывать годовые ставки процента, поэтому в двух предыдущих формулах годовая ставка процента делится на количество выплат в году (p).
Бескупонная облигация продаётся в момент выпуска со скидкой от номинальной стоимости (с дисконтом), а выкупается в момент T по номинальной стоимости. Бескупонными облигациями являются, например, государственные краткосрочные облигации (ГКО), которые размещаются путём продажи на аукционах по цене ниже номинальной стоимости. Доходность (к погашению) r бескупонной облигации, приобретённой по цене C, в том случае, если срок от даты покупки до даты погашения составляет d дней, вычисляется по формуле:
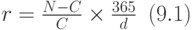
Здесь мы привели доходность за период существования облигации к годовой ставки процента с помощью простых процентов. Такого рода процедура корректна, так как чисто дисконтные облигации, как правило, бывают краткосрочными (до года), а тогда достаточно корректны и формула простых процентов и отсутствие каких-либо процедур дисконтирования (суммы N и C относятся к различным моментам времени).
Облигация с момента эмиссии до момента погашения обращается на рынке ценных бумаг, где имеет рыночную цену - {котировку. Эта цена меняется в зависимости от срока, прошедшего с момента эмиссии, и от общей конъюнктуры рынка. Обычно она указывается в процентах от номинальной стоимости облигации.
Рассмотрим, как определяется доходность облигаций. Пусть имеется купонная облигация с номинальной стоимостью N, которая будет погашена через T лет и по которой ежегодно  раз в год выплачиваются купонные процентные платежи от номинальной стоимости облигации по постоянной ставке j% годовых.
раз в год выплачиваются купонные процентные платежи от номинальной стоимости облигации по постоянной ставке j% годовых.
Предположим, что инвестор приобрёл купонную облигацию по цене Q в тот момент, когда до даты погашения осталось N лет ( ). Доходность приобретения облигации характеризуется так называемой доходностью к погашению (YTM - Yield to Maturity),
). Доходность приобретения облигации характеризуется так называемой доходностью к погашению (YTM - Yield to Maturity),  . Это ставка сложных процентов, при которой приведённая ценность всех доходов, полученных покупателем облигации, рассчитанная по ставке
. Это ставка сложных процентов, при которой приведённая ценность всех доходов, полученных покупателем облигации, рассчитанная по ставке  , равна цене покупки облигации Q. Составим уравнение для определения
, равна цене покупки облигации Q. Составим уравнение для определения  .
.
Приведённая ценность номинальной стоимости облигации N, которая будет получена через N~лет, равна  . Ежегодно покупатель получает по купонам сумму
. Ежегодно покупатель получает по купонам сумму 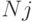 . Приведённая ценность этой ренты равна
. Приведённая ценность этой ренты равна 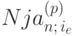 , если купонные платежи выплачиваются равными долями p раз в год (p-срочная рента), или
, если купонные платежи выплачиваются равными долями p раз в год (p-срочная рента), или  , если купонные платежи выплачиваются один раз в год. Следовательно, значение
, если купонные платежи выплачиваются один раз в год. Следовательно, значение  является корнем соответствующего уравнения:
является корнем соответствующего уравнения:

Разделив все члены этих уравнений на N, получим их окончательный вид:
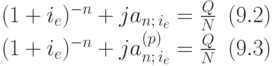
Пример 81. Облигация куплена по курсу 95% и будет погашена через 10 лет после покупки. Купонные платежи выплачиваются один раз в год в конце года, по ставке 5% годовых от номинальной стоимости облигации. Определить доходность приобретения этой облигации.
Решение. Купонные платежи образуют годовую ренту, поэтому значение  ищем, решая уравнение (91), которое в данном примере имеет вид:
ищем, решая уравнение (91), которое в данном примере имеет вид:
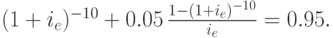
Решив это уравнение, получаем: 
Операции с облигациями
Облигация с купонным доходом может быть представлена как несколько бескупонных облигаций, которые принесут те же доходы и в те же сроки, что и купонная облигация. Покажем на примере, как это можно сделать.
Пример 82. Облигация с купонным доходом имеет номинальную цену  и погашается через 4 периода времени, в каждый из которых по купону выплачивается доход, равный
и погашается через 4 периода времени, в каждый из которых по купону выплачивается доход, равный  . Определим пакет бескупонных облигаций, которые принесут инвестору тот же доход в те же сроки, что данная бескупонная облигация.
. Определим пакет бескупонных облигаций, которые принесут инвестору тот же доход в те же сроки, что данная бескупонная облигация.
Решение. Изобразим денежный поток, соответствующий данной купонной облигации, на оси времени:
Пусть  - положительные числа, каждое из которых меньше D, и
- положительные числа, каждое из которых меньше D, и  Составим следующий пакет бескупонных облигаций:
Составим следующий пакет бескупонных облигаций:
1-я облигация: номинальная цена - D, цена приобретения -  (дисконт равен
(дисконт равен  ), срок погашения - первый период;
), срок погашения - первый период;
2-я облигация: номинальная цена - D, цена приобретения -  (дисконт равен
(дисконт равен  ), срок погашения - второй период;
), срок погашения - второй период;
3-я облигация: номинальная цена - D, цена приобретения -  (дисконт равен
(дисконт равен  ), срок погашения - третий период;
), срок погашения - третий период;
4-я облигация: номинальная цена -  , цена приобретения -
, цена приобретения -  (дисконт равен
(дисконт равен  ), срок погашения - четвертый период.
), срок погашения - четвертый период.
Изобразим потоки платежей по этим четырем бескупонным облигациям:
В момент 0 инвестор тратит на покупку этого пакета из четырёх бескупонных облигаций сумму N. В моменты 1, 2 и 3 он получает доход, равный D, а в момент 4 он получает сумму  . Таким образом, инвестор получает от составленного пакета бескупонных облигаций тот же доход и в те же сроки, что и от одной купонной облигации.
. Таким образом, инвестор получает от составленного пакета бескупонных облигаций тот же доход и в те же сроки, что и от одной купонной облигации.
Будем говорить, что купонная облигация и пакет бескупонных облигаций являются равноценными, если по ним инвестор получает одинаковый доход в одни и те же сроки. Из приведенного примера ясно, что для данной купонной облигации существует бесконечно много равноценных пакетов бескупонных облигаций, так как в качестве цен приобретения облигаций подходят любые положительные числа  ,
,  ,
,  , удовлетворяющие неравенству
, удовлетворяющие неравенству 
Арбитражная операция будет невозможна, если доходность купонной облигации и равноценного пакета бескупонных облигаций будут равны. Если в какой-либо момент доходность купонной облигации не равна доходности равноценного пакета бескупонных облигаций, то возникает возможность арбитражной операции.
Из определения доходности следует, что рыночная цена облигации или другой ценной бумаги обратно пропорциональна её доходности.
Если доходность купонной облигации выше доходности равноценного пакета бескупонных облигаций, то арбитражёр покупает купонную облигацию и продаёт равноценный пакет бескупонных облигаций. Арбитражёр получит прибыль, так как проданный им пакет бескупонных облигаций имеет большую рыночную цену, чем купонная облигация.
Если доходность купонной облигации, которую имеет арбитражёр, ниже доходности равноценного пакета бескупонных облигаций, то он продаст купонную облигацию и купит равноценный пакет бескупонных облигаций. Он получит прибыль, так как на рынке купонная облигация в этом случае дороже равноценного пакета.
Введем следующие важные понятия.
Рыночной (спот) процентной ставкой  для периода в T лет называется доходность бескупонной облигации, до погашения которой осталось T лет.
для периода в T лет называется доходность бескупонной облигации, до погашения которой осталось T лет.
Форвардной процентной ставкой называется ставка доходности бескупонной облигации в будущем периоде времени, рассчитанная по ставкам предыдущих периодов.
Покажем, как рассчитать форвардную ставку, при которой арбитражная операция с облигациями будет невозможна.
Пример 83. Рыночная ставка 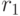 (на один год) равна 10%, рыночная ставка
(на один год) равна 10%, рыночная ставка 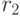 (на два года) равна 12%. Какова должна быть форвардная ставка
(на два года) равна 12%. Какова должна быть форвардная ставка  на три года, чтобы арбитражная операция с купонной облигацией, номинальной стоимости 100 руб. и до погашения которой осталось 3 года, была невозможна? Купонный доход равен 6% в год, рыночная цена облигации - 92 руб.
на три года, чтобы арбитражная операция с купонной облигацией, номинальной стоимости 100 руб. и до погашения которой осталось 3 года, была невозможна? Купонный доход равен 6% в год, рыночная цена облигации - 92 руб.
Решение. Арбитражная операция невозможна, если доходность купонной облигации и равноценного пакета бескупонных облигаций одинаковы. Это будет выполнено, если приведённая к настоящему моменту ценность пакета облигаций равна цене купонной облигации, то есть 92 руб.
Опишем равноценный пакет из трех бескупонных облигаций: номинальная цена первой и второй облигаций - 6 руб., третьей - 106 руб. Рыночная ставка  , поэтому рыночная цена первой бескупонной облигации в момент 0 равна:
, поэтому рыночная цена первой бескупонной облигации в момент 0 равна:

Рыночная ставка  , поэтому рыночная цена второй бескупонной облигации в момент 0 равна:
, поэтому рыночная цена второй бескупонной облигации в момент 0 равна:

Теперь мы можем определить рыночную цену третьей бескупонной облигации в момент 0:

Изобразим потоки платежей, связанные с пакетом бескупонных облигаций:
Этот пакет бескупонных облигаций равноценен купонной облигации: за него заплачено 92 руб., в каждый из трех лет получен доход 6% (6руб.), а в конце третьего года возвращена и номинальная цена облигации - 100 руб. Приведённая ценность пакета в момент 0 равна сумме:

Форвардная ставка r является корнем уравнения:
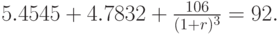
Решая это уравнение, находим значение форвардной ставки r на три года:

Выведем теперь в общем виде уравнение, определяющее форвардную ставку, исключающую возможность арбитражной операции с купонной облигацией и равноценным пакетом бескупонных облигаций.
Пусть до погашения купонной облигации с номиналом N осталось T периодов, в каждый из которых происходит выплата купонов:  . Известны рыночные ставки процента для бескупонных облигаций
. Известны рыночные ставки процента для бескупонных облигаций  , когда срок до погашения облигации равен
, когда срок до погашения облигации равен  год соответственно. Цена купонной облигации (в настоящий момент 0) равна P. Приведённая ценность равноценного пакета бескупонных облигаций равна сумме:
год соответственно. Цена купонной облигации (в настоящий момент 0) равна P. Приведённая ценность равноценного пакета бескупонных облигаций равна сумме:

Значение форвардной процентной ставки r является корнем уравнения:

Рассмотрим частный случай этого уравнения. Пусть в настоящий момент рыночная ставка процентов для бескупонной облигации на 1 год равна 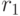 , на 2 года -
, на 2 года - 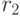 . Какова должна быть форвардная ставка r на 1 год в начале второго года, чтобы арбитражная операция была невозможна?
. Какова должна быть форвардная ставка r на 1 год в начале второго года, чтобы арбитражная операция была невозможна?
Если инвестор покупает бескупонную облигацию, номинальная стоимость которой равна N и которая выпущена на два года, то в начале двухлетнего периода он должен заплатить за неё сумму:

Инвестор может поступить иначе: купить в настоящий момент бескупонную облигацию со сроком 1 год; погасить её через год; на полученные деньги купить в начале второго года новую облигацию. Какова должна быть форвардная ставка r на один год для новой облигации, исключающая возможность арбитражной операции?
Во втором случае доход инвестора через два года будет равен N, если r удовлетворяет уравнению:

Подставив выражение для 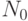 в последнее уравнение, получим равенство:
в последнее уравнение, получим равенство:

из которого получаем формулу для r:

Пример 84. Рыночные ставки процента для бескупонных облигаций составляют: 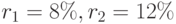 . Определим форвардную ставку
. Определим форвардную ставку  на 1 год в начале второго года, исключающую арбитражную операцию.
на 1 год в начале второго года, исключающую арбитражную операцию.
Решение. Форвардную ставку r определяем по формуле (9.5):

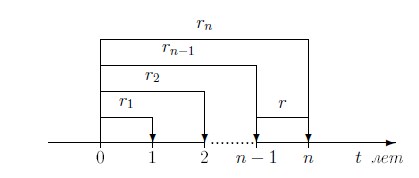
Рассмотрим теперь общую ситуацию. В момент 0 рыночные ставки процента для бескупонной облигации со сроком выкупа T лет равны  . Определим, какова должна быть форвардная ставка r для бескупонной облигации, эмитированной в момент
. Определим, какова должна быть форвардная ставка r для бескупонной облигации, эмитированной в момент  сроком на 1 год. Изобразим эту ситуацию на рисунке:
сроком на 1 год. Изобразим эту ситуацию на рисунке:
Форвардная ставка r определяется равенством доходов инвестора за N~лет от вложения денег в момент 0 на N~лет (нулевая стратегия) и какой-либо другой стратегии.
Нулевая стратегия. Чтобы получить в момент N сумму N, инвестор вкладывает в момент 0 сумму 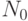 , которая определяется по формуле:
, которая определяется по формуле:

При равноценной стратегии вложения денег инвестор получит в момент N сумму N, вложив в момент 0 сумму 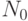 .
.
Рассмотрим две возможные стратегии.
Первая стратегия. Инвестор вкладывает в момент 0 сумму 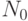 на срок
на срок  год и в конце
год и в конце  -го года получает сумму:
-го года получает сумму:

Эту сумму он вкладывает в момент  на 1 год под форвардную ставку r. В момент N будет получена сумма:
на 1 год под форвардную ставку r. В момент N будет получена сумма:
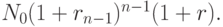
Из равноценности стратегий следует, что эта сумма должна быть равна сумме, полученной при реализации нулевой стратегии (N), то есть форвардная ставка r определяется из уравнения:
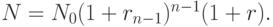
Подставив формулу для 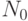 из нулевой стратегии, получим равенство:
из нулевой стратегии, получим равенство:

откуда получаем формулу для значения r:

Вторая стратегия. В момент 0 инвестор вкладывает сумму 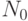 сроком на
сроком на 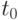 лет
лет  . В момент
. В момент 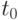 он получает сумму
он получает сумму
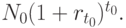
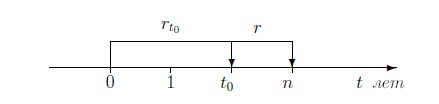
Эту сумму он вкладывает на оставшиеся  лет под форвардную ставку r, которая имеет место в момент
лет под форвардную ставку r, которая имеет место в момент 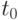 для бескупонной облигации, до погашения которой остается n-t_0~лет. Изобразим эту ситуацию на оси времени:
для бескупонной облигации, до погашения которой остается n-t_0~лет. Изобразим эту ситуацию на оси времени:
В момент N инвестор получит сумму, равную

Из равноценности стратегий следует, что эта сумма должна быть равна N, то есть форвардная ставка r определяется уравнением:
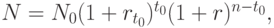
откуда получаем формулу для значения r:
![r=\sqrt[n-t_0]{\frac{(1+r_{n})^{n}}{(1+r_{t_0})^{t_0}}}-1\,\,\, (9.7)](/sites/default/files/tex_cache/e346dd6945c3ca6fb5bd9cc209f4bfdb.png)
Заметим, что формула (9.5) является частным случаем формулы (9.7) при 
Пример 81. Рыночные ставки процента для бескупонной облигации составляют: . Найдем форвардную ставку в двух случаях:
а) инвестор вкладывает деньги в начале первого года на 3 года и полученную сумму в начале четвёртого года на 1~год; какова должна быть форвардная ставка в начале четвёртого года для бескупонных облигаций со сроком выкупа 1 год?
б) инвестор вкладывает деньги в начале первого года на 2 года и полученную сумму в начале третьего года на 2~года; какова должна быть форвардная ставка в начале третьего года для бескупонных облигаций со сроком выкупа 2 года?
. Найдем форвардную ставку в двух случаях:
а) инвестор вкладывает деньги в начале первого года на 3 года и полученную сумму в начале четвёртого года на 1~год; какова должна быть форвардная ставка в начале четвёртого года для бескупонных облигаций со сроком выкупа 1 год?
б) инвестор вкладывает деньги в начале первого года на 2 года и полученную сумму в начале третьего года на 2~года; какова должна быть форвардная ставка в начале третьего года для бескупонных облигаций со сроком выкупа 2 года?
Решение. а) В этом случае  . Находим r по формуле (9.6):
. Находим r по формуле (9.6):

б) В этом случае 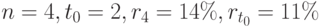 . По формуле (9.7) находим r:
. По формуле (9.7) находим r:
![r=\sqrt[4-2]{\frac{(1+0.14)^4}{(1+0.11)^2}}-1=\frac{1.2996}{1.11}-1=0.1708=%
17.08\%.](/sites/default/files/tex_cache/b57e190529fd8640ca2454f411021e59.png)