Сложные проценты

3.2 Основные задачи на сложные проценты

При использовании сложных процентов встречаются те же четыре типа задач, которые были рассмотрены для простых процентов. Задача первого типа встретилась в примерах 34 и 35. В следующих примерах решаются задачи остальных трех типов.

Пример 36. Какую сумму следует вложить в банк, выплачивающий , чтобы получить 3 000 руб. через 4 года 6 месяцев? .

Решение. Применим формулу (3.5) при :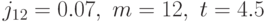

Из этого равенства находим значение P:

В предыдущем примере требовалось определить, какую сумму денег надо вложить в банк в настоящее время, чтобы получить сумму S через t лет в будущем. Решение такой задачи называется дисконтированием суммы S Величина вклада определяется формулой:

если начисление r% сложных производится один раз в год в течение t лет, и формулой:

если начисление процентов производится по ставке в течение t лет. Множитель называется дисконтным множителем.

Пример 37. Под какую процентную ставку следует вложить 5 000 руб., чтобы через 2 года получить 7 000 руб.?

Решение. Применим формулу (3.2) при S=7000, P=5000, t=2:

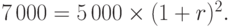
Преобразуем последнее равенство и определим из него значение r :

Пример 38. Банк начисляет ежегодно 8% сложных. Клиент положил в этот банк 20 000 руб. Через несколько лет на его счету была сумма, равная 29 386.56 руб. Сколько лет начислялись проценты

Решение. Преобразуем формулу (3.2) и получим формулу для t:

Используем эту формулу при S=29 386.56,P=20 000 и r=0.08:

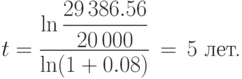
3.3 Непрерывное начисление сложных процентов

Мы видели (пример 35), что сумма, наращенная за t лет при постоянной процентной ставке , с увеличением числа m увеличивается (этот результат доказывается в общем виде в курсе высшей математики). При неограниченном увеличении m наращенная сумма стремится к конечному пределу:

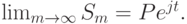
Этот факт даёт основание применять так называемое непрерывное начисление процентов по годовой ставке 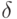. Наращенная за время t сумма определяется формулой:

Процентная ставка 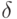в этом случае называется силой роста. Иногда силу роста обозначают . Значение для разных значений x можно вычислить с помощью финансового калькулятора или в Excel.

Из формулы (3.8) непосредственно следует формула дисконтирования капитала при непрерывном начислении процентов:

Заметим, что непрерывное начисление крайне редко используется на практике и широко используется в теории финансовых моделей.