|
Мне нужно изучить математическую статистику с нуля для обработки данных на компьютере. Читаю уже вторую лекцию, но пока ничего даже отдалённо близкого к моей цели не нахожу. Есть ли математическая статистика в дальнейших лекциях? Или я зря теряю время на изучение этого курса? У меня крайне ограниченный временной срок - я не могу терять время на самостоятельную проверку моего вопроса посредством изучения данного курса. |
Статистическое изучение взаимосвязей между социально-экономическими явлениями
12.3. Регрессионный анализ
12.3.1. Общие принципы построения регрессионных уравнений
На рисунке 12.2 приведены примеры корреляционного поля и формы связи, образованные скоплениями точек. Точки группируются возле некоторой линии, если связь показателей линейна, или кривой, если связь нелинейна. Эти линии называются линиями регрессии, а описывающие их аналитические выражения - уравнениями регрессии (рис. 12.2).
а - линейная связь;
б - параболическая связь;
в - гиперболическая связь;
г - нет связи (если две переменные практические не связаны между собой,
то моделью будет являться горизонтальная прямая)
Зная уравнение регрессии, можно приближенно оценить значение зависимой переменной Y при определенном значении Х. Причем точность такой оценки будет тем выше, чем теснее группируются точки фактических наблюдений относительно линии регрессии, т.д. точность модели регрессии определяется тем, насколько тесной является взаимозависимость признаков Х и Y.
Регрессионный анализ - это статистический метод исследования зависимости случайной величины Y от переменных Хj.
При построении парной регрессии (с одной факторной переменной) обычно используются следующие функции:
- линейная y = a0 + a1*xi
- степенная y = a0 + a1*xa1
- показательная y = a0 + a1x
- параболическая y = a0 + a1*xi + a2*x2
- гиперболическая y = a0 + a1/xi
- логарифмическая y = a0 + a1*lgxi
где а0 - свободный коэффициент уравнения регрессии;
а1 - параметр уравнения регрессии.
Однако в действительности любой результативный показатель испытывает воздействие не одного, как в случае парной корреляции, а нескольких факторов, поэтому зачастую строят модели множественной регрессии, которые принимают вид:
- линейная: y = a0 + a1*xi + a2*x2 + ak*xk
(наиболее часто встречающаяся модель);
- степенная: y = a0 *x1a1 *x2a2 ..... *xkak
- показательная y = ea0 + a1*xi + a2*x2 + ak*xk
- параболическая: y = a0 + a1*xi2 + a2*x22 + ak*xk2
- гиперболическая

где а0 - свободный коэффициент регрессии;
аj (j = 1, 2, …, k) - параметры регрессионного уравнения, называемые коэффициентами регрессии.
Для того чтобы правильно выбрать тип регрессионного уравнения, следует знать условный закон распределения зависимой переменной Y. На основе графика не всегда удается определить его однозначно, поэтому строят несколько регрессионных моделей, а затем по определенным критериям определяют лучшую модель. Если в проводимом исследовании можно ограничиться построением линейной модели, выбирают ее. Такая популярность и предпочтительность объясняется очень просто: математический аппарат линейных уравнений наиболее разработан, а сами модели легко интерпретируемы.
Критерием нахождения значений коэффициентов регрессии аj является следующее требование: сумма квадратов отклонений наблюдаемых "игреков" от "игреков", рассчитанных по уравнению регрессии, должна быть минимальной. Параметры регрессионной модели должны быть такими, чтобы на графике корреляционного поля линия регрессии оказалась там, где точки фактических наблюдений наибольшим образом сконцентрированы, т.д. проходила бы на минимальном удалении от них. В виде формулы это требование записывается следующим образом:
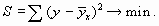
Метод нахождения значений коэффициентов регрессии по приведенному критерию называется методом наименьших квадратов (МНК).
12.3.2. Построение парного линейного уравнения
Если имеется только один факторный признак, строится так называемая парная регрессия, выражающаяся уравнением прямой
y = a0 + a1x
Коэффициент регрессии а1 показывает, на какую величину в среднем изменится результативный признак Y, если переменную Х увеличить на единицу ее собственного измерения.
Свободный член уравнения а0 характеризует усредненное влияние неучтенных в модели факторов (определяет начальные условия развития).
Для нахождения параметров уравнения прямой воспользуемся методом наименьших квадратов.
Для расчета параметров линейного уравнения регрессии решим следующую систему нормальных уравнений:
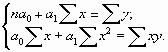
После решения системы и нахождения параметров а0 и а1 данные параметры подставляют в уравнение прямой. Рассчитанные по этому уравнению значения yk называются теоретическими (выравненными) значениями у.
Пример 12.3. Рассчитаем парный коэффициент корреляции и построим уравнение регрессии на основе следующих данных.
Стоимость основных фондов и выпуск продукции по группе заводов
| Номер завода | Стоимость основных фондов, млн руб., x | Выпуск продукции, млн руб., y |
|---|---|---|
| 1 | 6 | 2,4 |
| 2 | 8 | 4,0 |
| 3 | 9 | 3,6 |
| 4 | 10 | 4,0 |
| 5 | 10 | 4,5 |
| 6 | 11 | 4,6 |
| 7 | 12 | 5,6 |
| 8 | 13 | 6,5 |
| 9 | 14 | 7,0 |
| 10 | 15 | 5,0 |
| Итого | 108 | 47,2 |
Изобразим на графике координаты факторного и результативного признака точками, а затем соединим их между собой.
На поле корреляции появилась линия, которая по форме ближе всего к прямой.
Можно предположить, что между стоимостью основных фондов и выпуском продукции существует прямолинейная связь, которая выражается уравнением прямой y = a0 + a1x. Для определения параметров а0 и а1, используя метод наименьших квадратов, необходимо решить следующую систему нормальных уравнений:
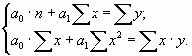
где n - численность совокупности (в нашем примере n - 10).
Проведем необходимые расчеты в следующей таблице.
| Номер завода | Стоимость основных фондов, млн руб., x | Выпуск продукции, млн руб., y | xy | x2 | yi |
|---|---|---|---|---|---|
| 1 | 6 | 2,4 | 14,4 | 36 | 2,692 |
| 2 | 8 | 4,0 | 32,0 | 64 | 3,537 |
| 3 | 9 | 3,6 | 32,4 | 81 | 3,958 |
| 4 | 10 | 4,0 | 40,0 | 100 | 4,380 |
| 5 | 10 | 4,5 | 45,0 | 100 | 4,380 |
| 6 | 11 | 4,6 | 50,6 | 121 | 4,802 |
| 7 | 12 | 5,6 | 67,2 | 144 | 5,224 |
| 8 | 13 | 6,5 | 84,5 | 169 | 5,646 |
| 9 | 14 | 7,0 | 98,0 | 196 | 6,068 |
| 10 | 15 | 5,0 | 75,0 | 225 | 6,460 |
| Итого | 108 | 47,2 | 539,1 | 1 236 | - |
Расчеты, проведенные в таблице, дали следующие результаты:

Следовательно, система уравнений для нахождения параметров прямой имеет вид:
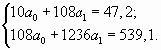
Решим ее.
Каждый член обоих уравнений поделим на коэффициенты при а0 и из второго уравнения вычтем первое:
- 4,72 = а0 + 10,8а1;
- 4,99 = а0 + 11,44 а1; 0,27 = 0,64 а1.
Определим параметр а1: 0.27/0.64 = 0.422.
Подставив значение а1 в первое уравнение, получим:
4,72 = а0 + 10,8*0,422, откуда а0 = 0,16.
Параметр а0 - свободный член уравнения: ух = 0,16, когда х = 0.
Получим:
а0 = 0,16; а1 = 0,422.
Параметр уравнения а1 показывает, что с увеличением стоимости фондов на 1 млн руб. выпуск продукции увеличивается в среднем на 0,422 млн руб. Линейное уравнение корреляционной связи будет иметь следующий вид:
y = 0.16 + 0.422x
Подставляя в это уравнение значения х, получим:
- при х = 6: у6 = 0,16 + 0,422 * 6 = 2,692;
- при х = 8: у8 = 0,16 + 0,422 * 8 = 3,537 и т.д.
Эти значения называются выравненными. Они приведены в последней колонке предыдущей таблицы.
Измерим тесноту связи между факторным и результативным признаками. Для расчета используем следующую формулу:
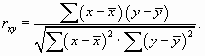
Расчет необходимых значений проведем в следующей таблице.
| Номер завода | x | y | (x - x) | (y - y) | (x - x)(y - y) | (x - x)2 | (y - y)2 | xy |
|---|---|---|---|---|---|---|---|---|
| 1 | 6 | 2,4 | -4,8 | -2,32 | +11,136 | 23,04 | 5,38 | 14,4 |
| 2 | 8 | 4,0 | -2,0 | -0,72 | +2,016 | 7,84 | 0,52 | 32,0 |
| 3 | 9 | 3,6 | -1,8 | -1,12 | +2,016 | 3,24 | 1,25 | 32,4 |
| 4 | 10 | 4,0 | -0,8 | -0,72 | +0,576 | 0,64 | 0,52 | 40,0 |
| 5 | 10 | 1,5 | 0,8 | 0,22 | +0,176 | 0,64 | 0,005 | 45,0 |
| 6 | 11 | 4,6 | +0,2 | -0,12 | -0,024 | 0,04 | 0,01 | 50,6 |
| 7 | 12 | 5,6 | +1,2 | 0,88 | +1,056 | 1,44 | 0,77 | 67,2 |
| 8 | 13 | 6,5 | +2,2 | +1,78 | +3,916 | 4,84 | 3,17 | 84,5 |
| 9 | 14 | 7,0 | +3,2 | +2,28 | +7,296 | 10,24 | 5,20 | 98,0 |
| 10 | 15 | 5,0 | +4,2 | +0,28 | +1,176 | 17,64 | 0,08 | 75,0 |
| Итого | 108 | 47,2 | - | - | +29,640 | 69,60 | 16,96 | 539,1 |
Связь между стоимостью основных фондов и выпуском продукции прямая и высокая.
Расчет коэффициента корреляции по следующей формуле даст такой же результат:
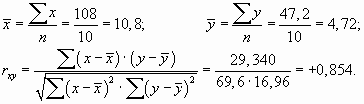
где 
 - среднее квадратическое отклонение результативного признака;
- среднее квадратическое отклонение результативного признака;
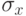 - среднее квадратическое отклонение факторного признака.
- среднее квадратическое отклонение факторного признака.
По данным таблицы проведем расчет:
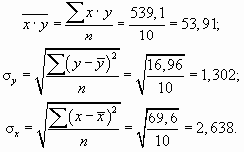
Подставим необходимые данные в формулу
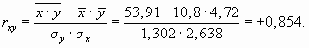
В случае нелинейной зависимости между признаками для измерения тесноты связи применяют корреляционное отношение, которое исчисляется по формуле
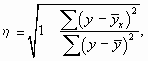
где у - фактические значения;
у - среднее значение;
yx - теоретические (выравненные) значения переменной величины.
Корреляционное отношение по своему абсолютному значению может принимать значения в пределах от 0 до 1.
12.3.3. Построение множественного уравнения регрессии
Теперь построим уравнение множественной регрессии. В нем результативный признак (у) будет зависеть не от одного факторного признака, а от двух (х1, х2).
Пример 12.4. В следующей таблице представлены данные о душевом доходе и потреблении мяса семей различного состава.
| Средний доход на члена семьи за месяц, руб., x1 (факторный признак) | Число членов семьи, x2 (факторный признак) | Душевое потребление мяса за месяц, кг, y (результативный признак) | yx1 | yx2 | x1x2 | x12 | x22 |  |
|---|---|---|---|---|---|---|---|---|
| 70 | 4 | 3,0 | 210,0 | 12,0 | 280 | 4 900 | 16 | 3,0 |
| 85 | 4 | 3,3 | 280,5 | 13,2 | 340 | 7 225 | 16 | 3,5 |
| 90 | 3 | 4,2 | 378,0 | 12,6 | 270 | 8 100 | 9 | 4,0 |
| 100 | 3 | 5,0 | 500,0 | 15,0 | 300 | 10 000 | 9 | 4,6 |
| 125 | 2 | 4,5 | 562,5 | 9,0 | 250 | 15 625 | 4 | 5,5 |
| 150 | 2 | 6,8 | 1 020,0 | 13,6 | 300 | 22 500 | 4 | 6,4 |
| 130 | 1 | 6,2 | 806,0 | 6,2 | 130 | 16 900 | 1 | 5,9 |
| 160 | 1 | 7,0 | 1 120,0 | 7,0 | 160 | 25 600 | 1 | 7,0 |
| Итого 910 | 20 | 40,0 | 4 877,0 | 88,6 | 2 030 | 110 850 | 60 | 40,0 |
| Среднее значение 113,75 | 2,5 | 5,0 | 609,63 | 11,075 | 253,75 |
Предполагая, что связь между у, х1 и х2 прямолинейная, воспользуемся методом наименьших квадратов и подставим данные таблицы в систему нормальных уравнений:
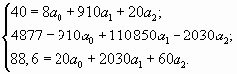
Решим ее.
Для решения системы нормальных уравнений разделим все члены уравнений на коэффициент при а0
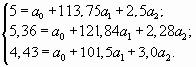
Вычтем теперь из первого уравнения второе и третье и получим
-0,36 = -8,06а1 + 0,27а2;
0,57 = 12,25а1 -0,5а2.
Разделим все члены уравнений на коэффициенты при а2 и вычтем из первого уравнения второе
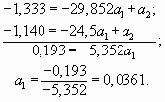
Подставив значение параметра а1 в уравнение, получим
-1,140 = -24,5 * 0,0361 + а2,
откуда
а2 = -1,140 + 0,8844 = 0,2556.
Аналогично определяем значение параметра а0, которое будет равно 1,5327.
Получим:
а0 = 1,5327; а1 = 0,0361; а2 = 0,2556.
Уравнение множественной регрессии, характеризующее зависимость потребления мяса от душевого дохода и числа членов семьи, будет иметь вид
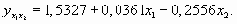
Параметр а1 показывает, что с ростом дохода на одного члена семьи на 1 руб. расходы на потребление мяса увеличиваются в среднем на 0,0361 руб., а параметр а2 показывает, что с увеличением размера семьи на 1 человека потребление мяса уменьшается в среднем на 0,2556 кг в расчете на одного человека.
Подставим в уравнение множественной регрессии эмпирические значения х1 и х2, получим теоретические значения y(х1х2) (см. последнюю графу таблицы).
При определении тесноты связи для множественной зависимости пользуются коэффициентом множественной (совокупной) корреляции, предварительно исчислив коэффициенты парной корреляции. Для нашего примера коэффициент множественной корреляции имеет вид
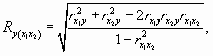
где  - парные коэффициенты корреляции.
- парные коэффициенты корреляции.
Коэффициент множественной корреляции может принимать значения в пределах от 0 до 1. Чем он ближе к 1, тем в большей мере учтены факторы, определяющие конечный результат.
Рассчитаем коэффициент множественной корреляции (табл.).
| (y - y) | (y - y)2 | (x1 - x1) | (x1 - x1)2 | (x2 - x2) | (x2 - x2)2 |
| -2 | 4,00 | -43,75 | 1 914,06 | +1,5 | 2,25 |
| -1,7 | 2,89 | -28,75 | 826,56 | +1,5 | 2,25 |
| -0,8 | 0,64 | -23,75 | 564,06 | +0,5 | 0,25 |
| 0 | 0,00 | -13,75 | 189,06 | +0,5 | 0,25 |
| 0,5 | 0,25 | 11,25 | 126,56 | -0,5 | 0,25 |
| 1,8 | 3,24 | 36,25 | 1 314,06 | -0,5 | 0,25 |
| 1,2 | 1,44 | 16,25 | 264,06 | -1,5 | 2,25 |
| 2,0 | 4,0 | 46,25 | 2 139,06 | -1,5 | 2,25 |
| 16,46 | 7 337 | - | - | 10 |
Для определения парных коэффициентов корреляции вычислим:
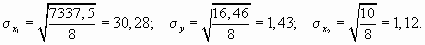
Парные коэффициенты корреляции определяются по следующим формулам:
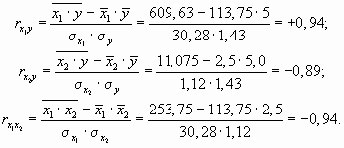
Подставим найденные значения в формулу коэффициента множественной корреляции
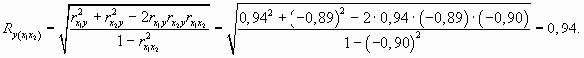
Сравнивая парные коэффициенты корреляции с коэффициентом множественной корреляции, мы видим, что связь между результативным признаком (у) и двумя факторами (х1 и х2) является более полной, чем с каждым фактором в отдельности.
Поскольку факторные признаки действуют не изолированно, а во взаимосвязи, то может возникнуть задача определения тесноты связи между результативным признаком и одним из факторных при постоянных значениях прочих факторов. Она решается при помощи частных коэффициентов корреляции. Например, при линейной связи частный коэффициент корреляции между х1 и у при постоянном х2 исчисляется по следующей формуле:
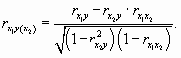
Частный коэффициент корреляции при изучении зависимости у от х2 при постоянном х1 определяется по формуле
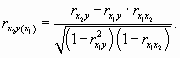
В нашем примере частный коэффициент корреляции между у и х1 при неизменном значении х2 равен
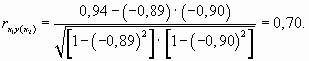
Частный коэффициент корреляции между у и х2 при неизменном значении фактора х1 равен
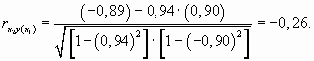
Если сравнить исчисленные коэффициенты частной корреляции с соответствующими коэффициентами парной корреляции, то окажется, что последние значительно больше первых, т.д. они преувеличивают меру связи между результативным и факторным признаком. Это объясняется тем, что факторы взаимно коррелируют между собой.
Коэффициенты же частной корреляции определяют действие каждого фактора при неизмененном значении остальных факторов. Поэтому они более точно определяют тесноту связи.
Вопросы для самоконтроля
- Перечислите основные исторические этапы становления статистики как науки.
- В каких государствах Древнего мира существовал статистический учет? Какие задачи он выполнял?
- Охарактеризуйте роль школы политических арифметиков в формировании статистики как науки.
- Каков вклад немецкой описательной школы в теорию статистики?
- В каких значениях может употребляться термин "статистика" в наше время?
- Дайте определение предмета изучения статистики.
- Почему к предмету изучения статистики относятся массовые явления и процессы общественной жизни?
- Какую роль играет в статистике закон больших чисел?
- Что такое статистическая закономерность? Приведите примеры наличия статистических закономерностей в экономической и социальной сферах.
- Почему количественные характеристики массовых явлений рассматриваются статистикой в неразрывной связи с их качественной стороной?
- В чем заключается метод статистики?
- Что изучают отраслевые статистики?
- Дайте определение статистической совокупности, приведите примеры статистических совокупностей.
- В чем отличие статистического признака от статистического показателя?
- Как организована государственная статистика в России?
- Какие задачи стоят перед государственной статистикой на современном этапе?
Вопросы для самоконтроля
- Назовите основные этапы проведения статистического наблюдения.
- Сформулируйте возможную цель статистического наблюдения деятельности промышленных предприятий России. Что в этом случае будет являться объектом, единицей наблюдения?
- В чем состоит отличие объекта наблюдения от единицы наблюдения?
- В каких случаях единица наблюдения будет совпадать с отчетной единицей? Приведите примеры.
- Назовите основные типы вопросов статистических анкет. Приведите примеры открытых и закрытых вопросов.
- Как влияют закрытые вопросы на сложность обработки результатов наблюдения?
- Что в себя включает программа наблюдения? Назовите основные требования, предъявляемые к программе наблюдения.
- Какие вопросы решает организационная подготовка статистического наблюдения?
- Охарактеризуйте основные формы статистического наблюдения.
- Почему наряду с ведением регистров населения проводится и перепись населения?
- Каковы особенности Всероссийской переписи населения 2002 г.?
- Перечислите виды статистического наблюдения.
- В чем состоят преимущества и недостатки несплошного и сплошного статистического наблюдения?
- Какие способы статистического наблюдения вы знаете?
- Что называется ошибкой регистрации? Приведите примеры таких ошибок.
- Когда возникают ошибки репрезентативности?
- Назовите мероприятия, позволяющие повысить точность статистического наблюдения.
Вопросы для самоконтроля
- Дайте определение статистической сводки и статистической группировки. В чем состоит их различие?
- Какие виды группировок применяются в статистической практике? Каково их назначение?
- Приведите примеры типологических и структурных группировок.
- Для каких целей строят аналитические группировки?
- Назовите виды рядов распределения. Приведите примеры таких рядов.
- Когда следует строить дискретные и интервальные вариационные ряды?
- Как рассчитать количество интервалов в случае построения интервального вариационного ряда с равными интервалами?
- К какому интервалу следует отнести единицу наблюдения при построении вариационного ряда, если ее значение попадает на границу интервала?
- Приведите примеры вариационных рядов с открытыми интервалами.
- В каких случаях для графического изображения вариационных рядов следует применять:
- полигон распределения;
- гистограмму?
- Как они строятся?
- Как строятся кумулята и огива распределения?
Вопросы для самоконтроля
- Что такое статистические таблицы?
- Охарактеризуйте подлежащее и сказуемое в статистических таблицах.
- Назовите виды таблиц по характеру разработки подлежащего и сказуемого. Приведите примеры таблиц из официальных статистических сборников.
- Какое правило построения и оформления статистических таблиц вы знаете?
- Какие виды графиков вы знаете?
- Какие типы графиков применяются для графического изображения структурной группировки?
- Перечислите виды статистических таблиц в зависимости от разработки подлежащего. Приведите примеры таких таблиц.
- Назовите виды статистических таблиц в зависимости от разработки сказуемого. Приведите примеры таких таблиц.
- Перечислите основные правила построения статистических таблиц.
- Из каких элементов состоит статистический график?
- Сформулируйте правила построения столбиковой, ленточной и фигурной диаграмм. Охарактеризуйте информативное значение этих графиков.
- Какие виды пиктографиков могут применяться в статистическом анализе?
- Приведите примеры диаграмм сравнения.
- Назовите цель применения радиальных диаграмм в статистическом анализе.
- Приведите примеры и сформулируйте правила построения основных биржевых статистических графиков.
Вопросы для самоконтроля
- Перечислите виды единиц измерения абсолютных статистических показателей.
- В каких единицах измерения происходит учет затрат труда на предприятии?
- В чем состоит особенность применения условных натуральных единиц измерения?
- Назовите единицы измерения относительных статистических показателей.
- Назовите виды относительных показателей, построенных в форме относительных величин.
- Охарактеризуйте взаимосвязь относительных показателей динамики, плана и выполнения плана.
- Как рассчитываются относительные величины динамики с переменной базой сравнения (цепные)?
- Опишите порядок расчета относительных величин динамики с постоянной базой сравнения (базисных).
- Как связаны между собой базисные и цепные относительные величины динамики?
- Приведите примеры расчета относительных показателей координации и структуры.
- Чему равна сумма относительных показателей структуры, рассчитанных по одной совокупности?
- Приведите примеры расчета относительных показателей интенсивности.
- Приведите примеры расчета относительных показателей сравнения.
- Какая основная цель преследуется при использовании относительных величин уровня экономического развития?
Вопросы для самоконтроля
- Дайте определение средней величины.
- Охарактеризуйте особенности и значение средних величин в анализе социально-экономических явлений.
- Какие виды средних величин вы знаете?
- Как влияет степень однородности совокупности на возможность использования средней арифметической величины в статистическом анализе?
- Какие свойства средней арифметической лежат в основе способа моментов?
- В каких случаях для расчета средней арифметической применяются формулы простой средней, а в каких - взвешенной средней?
- В каких случаях следует применять для расчета средней величины формулу средней гармонической?
- Приведите пример, в котором для расчета средней величины необходимо использовать формулу средней гармонической.
Вопросы для самоконтроля
- Дайте определение вариации признака. Может ли быть различной вариация значений признака в двух совокупностях, если их средние равны между собой?
- Перечислите абсолютные показатели вариации. Приведите формулы для их расчета.
- Перечислите относительные показатели вариации. Приведите формулы для их расчета.
- Какой аналитический смысл имеет коэффициент вариации?
- Что характеризует коэффициент осцилляции?
- Как по коэффициенту вариации можно судить о степени однородности исследуемой совокупности?
- Какие математические свойства дисперсии используются при ее расчете способом моментов?
- Назовите этапы расчета дисперсии способом моментов.
- Если все значения признака уменьшить в 5 раз, как изменится дисперсия признака?
Вопросы для самоконтроля
- В чем состоит отличие расчета моды в дискретных и интервальных рядах распределения?
- С помощью каких графиков можно определить значение моды?
- В чем состоит отличие расчетов медианы в дискретных и интервальных вариационных рядах?
- Если распределение признака близко к нормальному закону, как в этом случае связаны между собой среднее значение, мода и медиана?
- Какой аналитический смысл несут квартильные значения признака, децильные значения признака?
Вопросы для самоконтроля
- Дайте определение ряда динамики социально-экономических явлений.
- Какие вы знаете виды рядов динамики?
- Как проводится расчет среднего уровня в рядах динамики?
- Какие показатели изменения уровней рядов динамики вы знаете?
- Когда уровни динамического ряда становятся несопоставимыми? Приведите примеры. Что необходимо предпринять в этом случае?
- Расскажите о взаимосвязи цепных и базисных коэффициентов роста. Наблюдается ли подобная взаимосвязь у цепных и базисных темпов прироста?
- Что называется тенденцией динамического ряда?
- В чем состоит метод укрупнения интервалов?
- Расскажите о методе расчета скользящих средних.
- Перечислите основные математические функции, используемые при аналитическом выравнивании динамических рядов. В каких случаях применяется каждая из них?
- Как находятся параметры уравнения при выравнивании по линейной и показательной функциям, параболе и гиперболе?
- Какие виды периодических колебаний встречаются при анализе финансовых показателей?
- Перечислите основные методы расчета индексов сезонности.
Вопросы для самоконтроля
- Что представляет собой статистический индекс?
- Назовите виды статистических индексов.
- Чем отличаются индивидуальные индексы от сводных индексов?
- С какими весами обычно строят агрегатные индексы количественных показателей (качественных показателей)?
- Укажите взаимосвязь индексов стоимости, цен и физического объема.
- Как исчисляется средний арифметический индекс физического объема товарооборота?
- Как исчисляется средний гармонический индекс цен?
- С помощью каких индексов анализируется изменение среднего уровня качественного показателя?
- Опишите взаимосвязь индексов переменного, постоянного состава и индекса структурных сдвигов.
- Перечислите факторы, изменение которых показывают индексы переменного, постоянного состава и структурных сдвигов?
- Как используются индексы в анализе влияния отдельных факторов на изменение социально-экономических явлений?
Вопросы для самоконтроля
- Дайте определение генеральной и выборочной совокупностям.
- Какие теоремы теории вероятностей послужили теоретической основой выборочного метода?
- Какие преимущества и недостатки по сравнению со сплошным имеет выборочное наблюдение?
- Назовите виды и способы отбора единиц из генеральной совокупности.
- Как проводится случайный отбор единиц из генеральной совокупности?
- Как проводится механическая выборка?
- Какие преимущества имеет типический отбор по сравнению со случайным?
- В чем заключается сущность серийного отбора?
- Дайте определение малой выборки.
- Что показывает предельная ошибка выборки? Приведите формулы для ее расчета в случае оценивания генеральной доли и среднего значения признака.
- Как связаны между собой предельная и средняя ошибки выборки?
- Чему равна средняя ошибка выборки при использовании собственно случайной выборки и оценивании среднего?
- Как рассчитывается средняя ошибка выборки при типическом отборе?
- Как уменьшить ошибку собственно случайной выборки?
- Как определяется необходимая численность случайной выборки при заданной величине ошибки и доверительной вероятности?
- Каким образом происходит распространение результатов выборочного наблюдения на генеральную совокупность?
Вопросы для самоконтроля
- Приведите примеры функциональной, статистической и корреляционной зависимостей финансовых показателей.
- Каким требованиям должны удовлетворять исходные данные, чтобы к ним можно было применить методы корреляционно-регрессионного анализа?
- Какую роль в корреляционно-регрессионном анализе играет нормальный закон распределения?
- Что означает прямая связь между признаками? Приведите примеры прямой связи.
- Что означает обратная связь между признаками? Приведите примеры обратной связи.
- Какие задачи решают с помощью корреляционного анализа?
- В чем заключается сущность метода наименьших квадратов?
- Перечислите основные математические функции, используемые в качестве моделей регрессии.
- Назовите пределы изменения парного (линейного) коэффициента корреляции. Что он показывает?
- Назовите пределы изменения частного коэффициента корреляции. Что он показывает?
- Какой аналитический смысл несут свободный член уравнения и регрессионные коэффициенты при построении линейного регрессионного уравнения?
- Какой вид регрессионной модели следует использовать, если при равномерном возрастании независимой переменной значения результативного признака возрастают ускоренно?
- Какой вид регрессионной модели следует использовать, если результативный и факторный признаки возрастают или убывают одинаково приблизительно в арифметической прогрессии?


