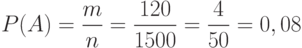Опубликован: 20.10.2016 | Доступ: свободный | Студентов: 916 / 431 | Длительность: 07:27:00
Тема: Математика
Специальности: Математик, Преподаватель
Лекция 3:
Определение вероятности
< Лекция 2 || Лекция 3 || Лекция 4 >
Основные теоретические сведения
Вероятностью события называется численная мера степени объективной возможности этого события.
Классическое определение вероятности
Вероятностью события А называется отношение числа исходов m, благоприятствующих наступлению события А, к числу n всех несовместных равновозможных элементарных исходов, образующих полную группу событий:
 |
( 1.8) |
где m – число исходов, n – число всех несовместных равновозможных элементарных исходов.
Из определения следует, что вероятность удовлетворяет условиям
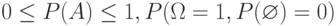
Классическое определение вероятности применяется только в следующих случаях:
- Число элементарных исходов конечно;
- Результаты всех испытаний и наблюденийравновозможны ;
- Все равновозможные события образуют полную группу попарно несовместных событий.
Пример решения задачи
Задача: Для новогодней лотереи отпечатали 1500 билетов, из которых 120 выигрышных. Какова вероятность того, что купленный билет окажется выигрышным?
< Лекция 2 || Лекция 3 || Лекция 4 >