Опубликован: 20.10.2016 | Доступ: свободный | Студентов: 916 / 431 | Длительность: 07:27:00
Тема: Математика
Специальности: Математик, Преподаватель
Лекция 1:
Элементы комбинаторики
Лекция 1 || Лекция 2 >
Ключевые слова: множества, перестановки, длина, подмножество, кортеж, Размещение, сочетания, выборка, перестановка с повторениями, размещение с повторением, сочетания с повторениями
Основные теоретические сведения
Упорядоченные множества (кортежи), состоящие из n различных элементов, называются перестановками (без повторений).
 |
( 1.1) |
где 
– число перестановок, 
– длина.
Упорядоченное подмножество m элементов (кортеж), составленное из всего множества, содержащего n элементов, называется размещением (без повторения).
 |
( 1.2) |
где 
– число размещений, – общее количество, 
– число всех выборов из n данных.
Сочетаниями (без повторений) из n элементов по m называется неупорядоченное подмножество (выборка), состоящее из m элементов, 48 взятых из множества, состоящего из n элементов.
 |
( 1.3) |
где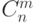 
– число сочетаний, – общее количество, – число всех выборов из n данных.
Кортеж, имеющий повторяющиеся элементы, называется перестановкой с повторениями.
 |
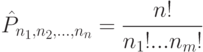( 1.4) |
где 
– число перестановок с повторениями, – общее количество, – число всех выборов из n данных.
Такое часто встречающееся число подсчетов вариантов называют размещением с повторением.
 |
( 1.5) |
где 
– число размещений с повторением, – общее количество, – число всех выборов из n данных.
Сочетаниями с повторениями называются соединения, содержащие n элементов, причем среди них могут быть одинаковые, а отличаются они хотя бы одним элементом, но не порядком.
 |
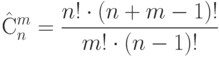( 1.6) |
где 
– число сочетаний с повторением, – общее количество, – число всех выборов из n данных.
Пример решения задачи
Задача: Сколькими способами из цифр 3, 5, 7, 9 можно составить различные четырехзначные числа?
Лекция 1 || Лекция 2 >
