Рынок как система обслуживания случайных потоков
[+]
Опубликован: 26.10.2016 | Доступ: свободный | Студентов: 406 / 20 | Длительность: 08:16:00
Темы: Экономика, Менеджмент
Специальности: Менеджер, Экономист
Лекция 1:

Математическая модель рынка
A
|
версия для печати
Лекция 1: 1234567 || Лекция 2 >
1.2.4. Простейший поток товаров и его свойства

Простейшим потоком товаров называется стационарный, ординарный поток без последействия. Простейший поток товаров полностью определяется и задаётся вероятностью поступления точно К партий товаров за время [0,t ).

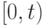Рассмотрим первый способ задания потока 1 последовательностью моментов наступления события, 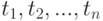t_1, t_2,...,t_n ( раздел 1.2.1)

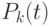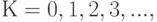Обозначим эту вероятность P_k (t) при К=0,1, 2,3,..., и t>0 .

Найдём выражение для 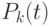P_k (t):

Поток заявок на товары

Рис. 1.2. Поток заявок на товары

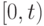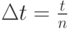
На рис. 1.2 изображен поток партий товаров на промежутке времени [0,t). Этот промежуток состоит из n равных отрезков длиною \Delta t=\frac {t}{n}

Рассмотрим малый отрезок времени длительностью 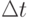\Delta t и вычислим вероятность того, что в этот промежуток времени поступит хотя бы одна партия товара. По определению, параметром потока мы назвали предел отношения:

\lambda=\frac{ \lim_{ \Delta t \to 0} P_{K \geq 1} (t_0, t_0+ \Delta t) }{ \Delta t}=\frac{ \lim_{ \Delta t\to 0}P_{K \geq 1} (\Delta t)}{\Delta t}

Следовательно, с точностью до бесконечно малых высшего порядка, при 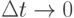\Delta t \rightarrow 0 можно считать вероятность того, что в промежуток времени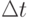 \Delta t

поступит хотя бы одна партия товара:

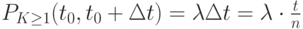
P_{K \geq 1} (t_0, t_0+ \Delta t) = \lambda \Delta t= \lambda \cdot \frac{t}{n}

а вероятность того, что не поступит ни одной партии товаров

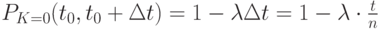
P_{K = 0} (t_0, t_0+ \Delta t) = 1-\lambda \Delta t= 1-\lambda \cdot \frac{t}{n}

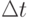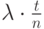Так как по определению простейший поток - это поток без последействия, то вероятности поступления партий товаров в неперекрывающиеся промежутки времени независимы. Следовательно, n промежутков времени можно рассматривать как n независимых опытов, в каждом из которых за промежуток времени \Delta tmath> может поступить партия товаров с вероятностью \lambda \cdot \frac{t}{n}.

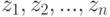Вероятность того, что среди n промежутков будет ровно К, в которые поступают партии товаров, (второй способ задания последовательностью промежутков времени между событиями моментами z_1, z_2,...,z_n) можно определить по теореме о повторении опытов (по формуле Бернулли) из выражения

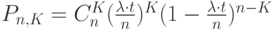
P_{n,K}=C_n^K(\frac{\lambda \cdot t}{n})^K(1-\frac{\lambda \cdot t}{n})^{n-K}

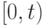При достаточно большом числе промежутков времени n эта вероятность приблизительно равна вероятности поступления точно К партий товаров в промежуток времени [0,t ), так как вероятность поступления двух или более вызовов в промежуток 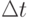\Delta t имеет пренебрежимо малую вероятность (простейший поток ординарный!).

Чтобы найти точное значение 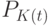P_{K(t)}, нужно перейти к пределу при n \to \infty:

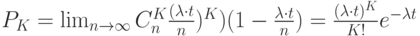
P_K= \lim_{n\to \infty } C_n^K \frac{(\lambda \cdot t}{n})^K)(1-\frac{\lambda \cdot t}{n})=\frac{( \lambda \cdot t)^K}{K!}e^{- \lambda t}

Распределение вероятностей 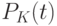P_K(t) называется распределением Пуассона. Чтобы убедиться, что последовательность вероятностей 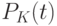P_K(t) представляет собой ряд распределений, необходимо показать, что сумма всех вероятностей 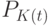P_{K(t)} равна единице. Действительно, согласно формуле ряда Тейлора

\sum_{K-0}^{z} P_K(t)=\sum_{K-0}^{z} \frac{(x)^K}{K!}=e^x

получим:

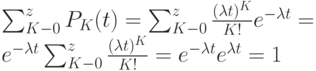
\sum_{K-0}^{z} P_K(t)=\sum_{K-0}^{z} \frac{( \lambda t)^K}{K!}e^{- \lambda t}=\\ e^{- \lambda t}\sum_{K-0}^{z} \frac{( \lambda t)^K}{K!}=e^{- \lambda t}e^{ \lambda t}=1

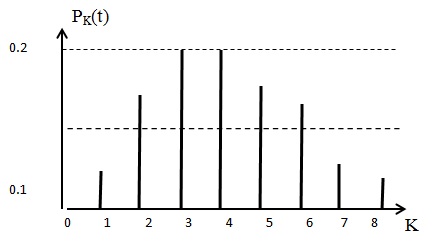
Чтобы построить распределение Пуассона, необходимо для всех К

рассчитать 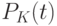P_K(t). Это распределение дискретной случайной величины. Например, при \lambda \cdot t=4 распределение имеет следующий вид (рис. 1.3):

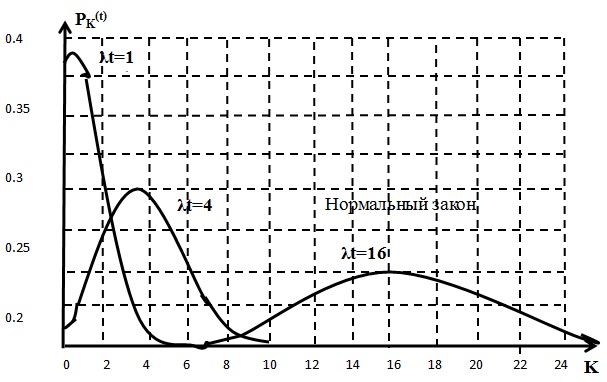
Огибающие распределения

Рис. 1.3. Огибающие распределения

Огибающие распределения Пуассона при различных \lambda \cdot t имеют следующий вид (рис. 1.4):

Огибающие распределения

Рис. 1.4. Огибающие распределения

Как видно из рисунка, с возрастанием огибающая принимает всё более

симметричный вид. При \lambda \cdot t \geq 10 имеет место хорошее совпадение между огибающей закона распределения Пуассона и нормальным законом распределения (который является законом распределения непрерывной случайной величины), формула и график которого:

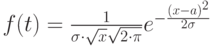
f(t)=\frac{1}{ \sigma \cdot \sqrt{x} \sqrt{2 \cdot \pi } }e^{-\frac{(x-a)^2}{2 \sigma }}

Нормальный закон распределения

Рис. 1.5. Нормальный закон распределения

1.2.5. Математическое ожидание и дисперсия простейшего потока вызовов

Определим математическое ожидание числа партий товаров, поступающих за время 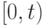[0,t ):

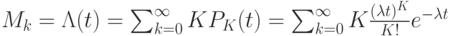M_k= \Lambda (t)= \sum_{k=0}^{ \infty } KP_K(t)=\sum_{k=0}^{ \infty }K\frac{( \lambda t )^K}{K!}e^{- \lambda t} - выражение начального момента первого порядка.

Первый член суммы при 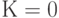К=0 равен нулю, следовательно

суммирование можно начинать с К=1:

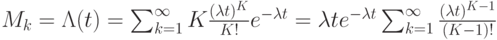
M_k= \Lambda (t)= \sum_{k=1}^{ \infty }K\frac{( \lambda t )^K}{K!}e^{- \lambda t}= \lambda te^{- \lambda t}\sum_{k=1}^{ \infty }\frac{( \lambda t)^{K-1}}{(K-1)!}

Обозначая 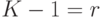K-1=r , с помощью ряда Маклорена получим:

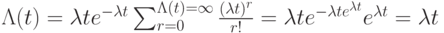
\Lambda (t)= \lambda te^{- \lambda t} \sum_{r=0}^{ \Lambda (t)= \infty } \frac{( \lambda t)^r}{r!}= \lambda te^{- \lambda te^{ \lambda t}} e^{ \lambda t}= \lambda t

Но с другой стороны:

\Lambda (t) = \mu \cdot t - по определению для стационарного потока.

Следовательно, для простейшего потока интенсивность численно равна

параметру - \mu = \lambda.

Дисперсию случайной величины, распределённой по закону Пуассона, будем определять из выражения:

D_k= \sum_{K=0}^{ \infty } [K-M_K]^2P_K= \alpha_2-M_k^2

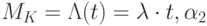где M_K - математическое ожидание, M_K =\Lambda (t)=\lambda \cdot t , \alpha_2 - начальный момент второго порядка.

По определению:

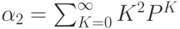
\alpha_2= \sum_{K=0}^{\infty} K^2 P^K

\alpha_2= \sum_{K=0}^{\infty}K^2}\frac{(\lambda \cdot t)^K}{K!} e^{- \lambda \cdot t}= \\ \lambda \cdot t \sum_{K=1}^{\infty} K \cdot \frac{(\lambda \cdot t)^{K-1}}{(K-1)!}} \cdot e^{- \lambda \cdot t}= \\ \lambda \cdot t \sum _{K=1}^{\infty}(K-1+1) \cdot \frac {(\lambda \cdot t)^{K-1}}{(K-1)!}}= \\ \lambda \cdot t [ \lambda \cdot t \sum _{K=1}^{\infty} (K-1) \cdot \frac {(\lambda \cdot t)^{K-1}}{(K-1)!}} - \frac {(\lambda \cdot t)^{K-1}}{(K-1)!}}]

Уже было доказано, что:

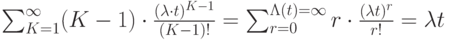
\sum_{K=1}^{ \infty } (K-1)\cdot \frac{ (\lambda \cdot t)^{K-1}}{(K-1)!}= \sum_{r=0}^{ \Lambda (t)= \infty } r\cdot \frac{ (\lambda t)^r }{r!}= \lambda t

Кроме того:

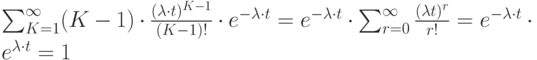
\sum_{K=1}^{ \infty } (K-1)\cdot \frac{ (\lambda \cdot t)^{K-1}}{(K-1)!}\cdot e^{- \lambda \cdot t}=e^{- \lambda \cdot t}\cdot \sum_{r=0}^{ \infty }\frac{( \lambda t)^r}{r!}=e^{- \lambda \cdot t}\cdot e^{ \lambda \cdot t}=1

Следовательно:

\alpha_2=\lambda \cdot t\cdot [\lambda \cdot t + 1]

Дисперсия простейшего потока:

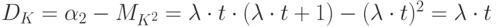
D_K=\alpha_2 - M_{K^2}=\lambda \cdot t \cdot (\lambda \cdot t +1)-( \lambda \cdot t)^2=\lambda \cdot t

Таким образом, дисперсия простейшего потока вызовов равна

математическому ожиданию:

M_K=D_K=\lambda \cdot t

Из этого свойства простейшего потока следует важный для практики вывод: относительное колебание простейшего потока вызовов тем меньше,

чем больше его математическое ожидание.

Относительное колебание оценивается коэффициентом вариации отношением:

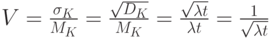
V= \frac{ \sigma _K}{M_K}=\frac{ \sqrt{D_K} }{M_K}= \frac {\sqrt{ \lambda t} }{ \lambda t}=\frac {1}{\sqrt{ \lambda t} }

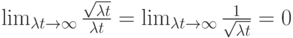
\lim_{ \lambda t \to \infty } \frac {\sqrt{ \lambda t} }{ \lambda t}= \lim_{\lambda t \to \infty} \frac {1}{ \sqrt{ \lambda t}} = 0

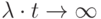
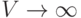то есть при \lambda \cdot t \rightarrow \infty V \rightarrow \infty;

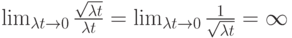
\lim_{\lambda t \to 0 } \frac {\sqrt{ \lambda t} }{ \lambda t}= \lim_{\lambda t \to 0} \frac {1}{\sqrt{ \lambda t}}= \infty

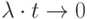
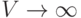то есть при \lambda \cdot t \rightarrow 0 V \rightarrow \infty .

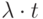\lambda \cdot t - математическое ожидание числа вызовов, поступающих за [0, t ).

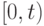Отсюда эффективность системы массового обслуживания выше, чем больше

интенсивность поступающего на систему потока товаров. Это фундаментальное свойство случайных потоков событий широко используется в системах массового обслуживания: в телекоммуникациях для концентрации потоков вызовов строят телефонные станции большой ёмкости и коммутационные узлы; в торговле - супер- и гипермаркеты; на транспорте крупные аэропорты и вокзалы.

Объединение и разъединение независимых простейших потоков:

Объединение независимых простейших потоков с параметрами

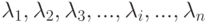\lambda_1 , \lambda _2 , \lambda _3 ,... , \lambda _i ,... ,\lambda_n тоже будет простейшим потоком с параметром 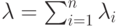\lambda = \sum_{i=1}^{n} \lambda _i, равным сумме параметров объединяемых потоков.

Рекуррентная формула Пуассона:

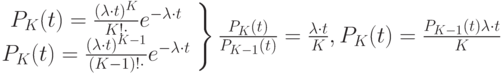
\left. \begin{array}{ccc} P_K (t) = \frac{ (\lambda \cdot t)^K}{K! \cdot}e^{- \lambda \cdot t} \\ P_K (t) = \frac{ (\lambda \cdot t)^{K-1}}{(K-1)! \cdot}e^{- \lambda \cdot t}\\ \end{array} \right\} \frac{P_K(t)}{P_{K-1}(t)}=\frac{ \lambda \cdot t}{K}, P_K(t)=\frac{P_{K-1}(t) \lambda \cdot t}{K}

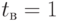Обозначим t_в - среднюю длительность пребывания в системе одного товара (обычно принимается t_в=1). Разделим и умножим 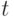t на t_в:

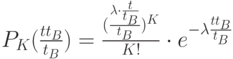
P_K(\frac{tt_B}{t_B})=\frac{(\frac{ \lambda \cdot \frac{t}{t_B}}{t_B})^K}{K!}\cdot e^{- \lambda \frac{tt_B}{t_B}}

Введём n=\frac{t}{t_B} и получим:

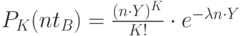
P_K(nt_B)=\frac{(n\cdot Y)^K}{K!}\cdot e^{- \lambda n\cdot Y}

где Y - интенсивность предложения.

Если 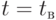t=t_в , то

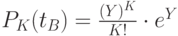
P_K(t_B)=\frac{(Y)^K}{K!}\cdot e^Y

Учитывая сказанное, для более эффективного обслуживания потоков товаров желательно производить их объединение.

Без доказательства отметим ещё одно интересное свойство простейшего потока: при суммировании большого числа независимы ординарных стационарных потоков с практически любым последействием, получается поток, сколь угодно близкий к простейшему.

Аналогия: при суммировании большого числа независимых случайных величин, подчинённых практически любым законам распределения, получается величина, приближённо распределённая по нормальному закону.

Дальше >>
Лекция 1: 1234567 || Лекция 2 >

Вопросы и ответы

вопросов: 0