Стационарные временные ряды, модели авторегрессии - скользящего среднего

10.3. Процессы авторегрессии - скользящего среднего

Скомбинируем процесс скользящего среднего с линейным разностным уравнением для получения АРСС-модели.

Рассмотрим разностное уравнение -го порядка

(10.6)

Пусть теперь будет СС()-процесс, представленный формулой (10.5). Тогда

(10.7)

т.е. получаем формулу (9.2), если нормализовать (10.7) так, чтобы коэффициент всегда был равен единице.

Если все характеристические корни выражения (10.6) находятся внутри единичного круга (см. условие устойчивости в главе 9), то 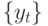называется АРСС-моделью для процесса .

Авторегрессионная часть модели состоит из разностного уравнения с правой частью Остальная часть уравнения представлена скользящим средним - процессом вида (10.5). Если авторегрессионная часть содержит лагов, а скользящее среднее лагов (запаздываний), то это АРСС()-модель.

Если , то получаем чистое уравнение авторегрессии (AP()-модель). И если , имеем модель скользящего среднего порядка (СС()-модель). В АРСС-моделях можно предполагать, что как порядок , так и могут быть равны . Если характеристические корни лежат внутри единичного круга не для самого ряда 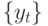, а для некоторой разности , то процесс называется интегрированным, а модель (10.6) - авторегрессионной интегрированной скользящего среднего моделью (АРИСС()-моделью).

Рассматривая (10.7) как разностное уравнение, решим его относительно , используя последовательность . Для АР(1)-модели

такое представление получено в главе 9

Для общих АРСС()-моделей перепишем (10.7), используя оператор запаздывания (сдвига) на единицу ,

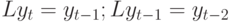и т.д.

Получаем:

(10.8)

Отсюда получим формальное решение:

(10.9)

Можно доказать, что для существования выражения (10.9) необходимо, чтобы характеристические корни многочлена располагались вне единичного круга.

Это и будут условия устойчивости стохастического разностного уравнения (10.8). Будет также показано, что условия устойчивости необходимы для стационарности временного ряда .

В экономике типичной является ситуация, когда для наблюдения доступна только одна реализация случайного процесса, а не множество реализаций. В таких случаях приходится иметь дело с единственным временным рядом, а не с множеством временных рядов, отражающих данный процесс за один и тот же промежуток времени.

Однако, если 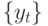- стационарный ряд, то среднее, дисперсия и автокорреляция могут быть аппроксимированы достаточно длинным усреднением по времени единственной серии реализаций. Это означает, что среднее и дисперсия процесса имеют одно и то же значение в каждый момент времени. Более строго стохастический процесс, имеющий конечные среднюю и дисперсию, ковариационно стационарный (стационарный в слабом смысле), если для всех и

Такие процессы в литературе также называют стационарными второго порядка, а величины 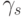- автоковариациями -го порядка.

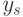Определим автокорреляции -го порядка между и 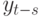по формуле

(10.13)

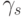где и 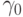определены в (10.12). Очевидно, что .