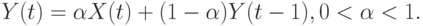НОУ ИНТУИТ | Введение в эконометрику. Лекция 6: Сглаживание временных рядов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 10.09.2016 | Доступ: свободный | Студентов: 947 / 166 | Длительность: 15:27:00

Тема: Экономика

Специальности: Менеджер, Руководитель, Экономист, Бухгалтер

|

Вам нравится? Нравится 27 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

6.4. Простое экспоненциальное сглаживание

Выше рассмотрены симметричные фильтры для сглаживания временных рядов. Вместе с ними широкое распространение при прогнозировании временных рядов получили асимметричные фильтры. Простейший из них - скользящая средняя, которая заменяет последнее значение ряда внутри интервала сглаживания,

(6.22)

Из формулы (6.22) следует простая рекуррентная формула

(6.23)

Первое слагаемое в формуле (6.23) указывает на то, что процесс обладает инерцией развития. Второе слагаемое отражает последние изменения в процессе, причем вес, с которым учитывается новое значение, зависит от ширины интервала сглаживания и равен 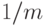1/m .

В предложенном методе (см. (6.22)) прошлые значения временного ряда выбирались с постоянным весом. Однако естественно прогнозировать будущие значения ряда с учетом устаревания информации. Один из приемов сглаживания ряда, позволяющих учитывать устаревание данных, является придание веса a текущему наблюдению и веса $1 - \alpha$ предыдущему сглаженному значению ряда

$Y(t) = \alpha X(t) + (1 - \alpha )Y(t - 1), 0 < \alpha <1.$

(6.24)

Если формулу (6.24) последовательно применить к 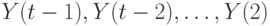$Y(t - 1), Y(t - 2), \dots, Y(2)$ , то получим

(6.25)

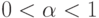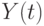Так как $0 < \alpha < 1$ , веса при X(t - k) быстро уменьшаются с ростом и влияние на Y(t) падает. Аналогично (6.23) можно переписать формулу (6.24)

$Y(t) = Y(t - 1) + \alpha (X(t) - Y(t - 1)), 0 < \alpha < 1.$

(6.26)

Из формулы (6.26) видно, что a является коэффициентом поправки на "новизну" в сглаженном временном ряде 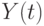Y(t) . Отметим, наконец, что за 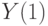Y(1) обычно принимают X(1) и процедуру сглаживания начинают со второго члена ряда.

Для простой экспоненциальной средней, в предположении о независимости членов исходного ряда и постоянности дисперсии 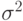$\sigma ^{2}$ , можно вывести формулу для дисперсии сглаженного ряда

$D(Y(t)) = D(\alpha X(t) + (1 - \alpha )Y(t - 1)) = D(\alpha X(t)) + D((1 - \alpha )Y(t - 1)) =\\ = \alpha ^{2}D(X(t)) + (1 - \alpha )^{2}D(Y(t - 1)) = \alpha ^{2}\sigma ^{2} + (1 - \alpha )^{2}D(Y(t - 1)).$

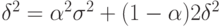Так как $\delta ^{2} = D(Y(t)) = D(Y(t - 1))$ , то $\delta ^{2} =\alpha ^{2}\sigma ^{2} + (1 - \alpha )2\delta ^{2}$ . Отсюда Следовательно, дисперсия сглаженного ряда меньше дисперсии исходного ряда.

Теперь рассмотрим вопрос о выборе параметра \alpha . Во многих руководствах рекомендуется выбирать a из промежутка [0,1; 0,3].

Однако в работе С. Макридакиса рассмотрены примеры, когда лучшие результаты сглаживания были получены при 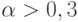$\alpha > 0,3$ . Поэтому в последних статистических пакетах (например, в пакете STATISTICA) предлагается находить оптимальное значение параметра $\alpha$ методом перебора значений с заранее выбранным шагом h.

Метод простого экспоненциального сглаживания получил популярность главным образом благодаря его привлекательности как инструмента прогноза и простоте реализации. Так, С. Макридакис показал, что простое показательное сглаживание было лучшим выбором для прогноза "один период вперед" из числа 24 других методов. Таким образом, независимо от теоретической модели процесса, лежащей в основе наблюдаемого временного ряда, простое показательное сглаживание часто дает весьма точные прогнозы.

Дальше >>

Авторизоваться

Введение в эконометрику

Сглаживание временных рядов

6.4. Простое экспоненциальное сглаживание

Вопросы и ответы