Подбор параметра
Существует класс задач, связанных с численным подбором решения какого-либо уравнения. Часто эти уравнения являются трансцендентными, для которых не существует аналитического решения. В этом случае решение ищется путём поиска корня уравнения по некоторому алгоритму.
В качестве простого примера рассмотрим поиск корней уравнения, описанного формулой 8.1.
 |
( 8.1) |
Можно привести это уравнение к "каноническому" виду (формула 8.2).
 |
( 8.2) |
Таким образом, изменяя значение  по каким-то правилам, нужно найти такое значение, при котором левая часть уравнения станет равна 0 с "машинной" точностью (поскольку вещественные числа в компьютере никогда не могут быть в точности равны).
по каким-то правилам, нужно найти такое значение, при котором левая часть уравнения станет равна 0 с "машинной" точностью (поскольку вещественные числа в компьютере никогда не могут быть в точности равны).
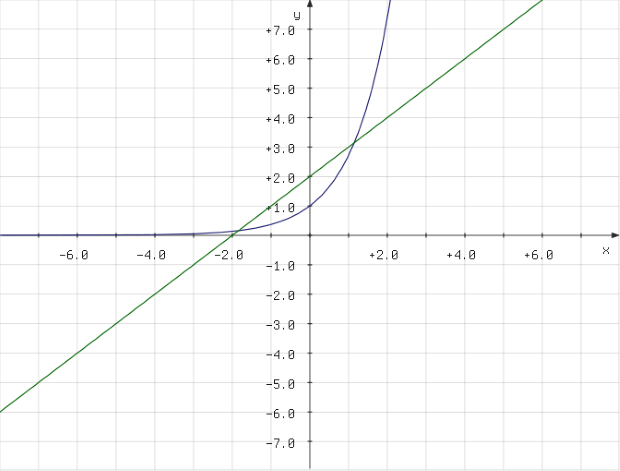
Прежде всего нужно убедиться в том, что решение существует. Для этого достаточно с помощью любой программы, позволяющей рисовать графики функций (например, средствами Gnumeric) получить на одном рисунке графики левой и правой части первоначального уравнения (рис. 8.1).
Из графиков видно, что решение существует, более того, существует два решения. Теперь рассмотрим применение Gnumeric для поиска корней нашего уравнения.
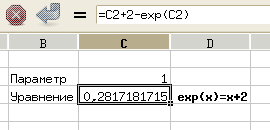
Сначала сформируем таблицу исходных данных, в которой укажем какое-то начальное значение искомой функции (для "канонического" вида уравнения), и введём формулу для функции (рис. 8.2).
В ячейке C2 записано начальное значение параметра  , в C3 – формула для вычисления значения функции, а в D3 – исходное уравнение для справки.
, в C3 – формула для вычисления значения функции, а в D3 – исходное уравнение для справки.
Задача состоит в том, чтобы подобрать такое значение в C2, чтобы результат в C3 стал равным 0.
Для решения задачи используем инструмент "Подбор параметра..." (возможны также названия "Поиск цели" или "Goal Seek"), выбрав с помощью главного меню команду "Сервис/Подбор параметра..." (рис. 8.3).
В строке "Установить ячейку:" указываем адрес ячейки, в которой записана формула функции, в строке "Изменяя ячейку:" указываем адрес ячейки, содержащей значение параметра  , а в строке "До значения:" указываем целевое значение функции.
, а в строке "До значения:" указываем целевое значение функции.
Если не задавать значения минимум и максимума параметра при поиске решения, программа найдёт только одно из возможных решений (если их несколько). Как видно из рис. 8.1, одно решение находится в области положительных значений  , другое – в области отрицательных значений.
, другое – в области отрицательных значений.
Нажатие на кнопку "Применить" запустит процесс поиска и в этом же окне будет показан результат (рис. 8.4).
Чтобы получить второе решение, нужно определить интервал значений x для поиска и снова запустить процесс (рис. 8.5).
Вообще говоря, достаточно указать только максимальное значение (например, искать все значения меньше 0), но для определённости зададим интервал значений от -10 до 0.
"Подбор параметра" в Gnumeric – очень простой в использовании инструмент, но для получения правильных результатов нужно соблюдать некоторые правила:
- Предварительно убедиться в том, что решение существует;
- Если решение не единственное, определить, какое из решений требуется по условию задачи;
- Интервалы для значений параметра выбирать так, чтобы в каждом интервале было только одно решение.