НОУ ИНТУИТ | Компьютерная математика с Maxima. Лекция 8: Реализация некоторых численных методов

Компания ALT Linux

Опубликован: 24.03.2015 | Доступ: свободный | Студентов: 550 / 136 | Длительность: 19:00:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

8.3 Методы решения систем линейных уравнений

8.3.1 Общая характеристика и классификация методов решения

Рассмотрим систему линейных алгебраических уравнений (сокращенно — СЛАУ):

$A \cdot \bar x = \bar f,$

( 8.1)

где

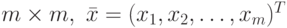— матрица $m \times m,\ \bar x = {({x_1},{x_2},\dots,{x_m})^T}$ — искомый вектор, 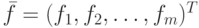$\bar f = {({f_1},{f_2},\dots,{f_m})^T}$ — заданный вектор. Будем предполагать, что определитель матрицы A отличен от нуля, т.е. решение системы (8.1) существует.

Методы численного решения системы (8.1) делятся на две группы: прямые методы ("точные") и итерационные методы.

Прямыми методами называются методы, позволяющие получить решение системы (8.1) за конечное число арифметических операций. К этим методам относятся метод Крамера, метод Гаусса, LU-метод и т.д.

Итерационные методы (методы последовательных приближений) состоят в том, что решение системы (8.1) находится как предел последовательных приближений 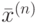${\bar x^{(n)}}$ при $n \to \infty$ , где — номер итерации. При использовании методов итерации обычно задается некоторое малое число $\varepsilon$ и вычисления проводятся до тех пор, пока не будет выполнена оценка $\left\| {{{\bar x}^{(n)}} - \bar x} \right\| < \varepsilon$ . К этим методам относятся метод Зейделя, Якоби, метод верхних релаксаций и т.д.

Следует заметить, что реализация прямых методов на компьютере приводит к решению с погрешностью, т.к. все арифметические операции над переменными с плавающей точкой выполняются с округлением. В зависимости от свойств матрицы исходной системы эти погрешности могут достигать значительных величин.

8.3.2 Метод Гаусса

Запишем систему (8.1), в развернутом виде

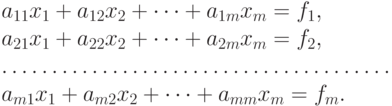
${{a_{11}}{x_1} + {a_{12}}{x_2} + \dots + {a_{1m}}{x_m} = {f_1},} \\ {{a_{21}}{x_1} + {a_{22}}{x_2} + \dots + {a_{2m}}{x_m} = {f_2},} \\ {\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots} \\ {{a_{m1}}{x_1} + {a_{m2}}{x_2} + \dots + {a_{mm}}{x_m} = {f_m}.}$

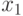Метод Гаусса состоит в последовательном исключении неизвестных из этой системы. Предположим, что ${a_{11}} \ne 0$ . Последовательно умножая первое уравнение на $- \cfrac{{{a_{i1}}}}{{{a_{11}}}}$ и складывая с -м уравнением, исключим x_1 из всех уравнений кроме первого. Получим систему

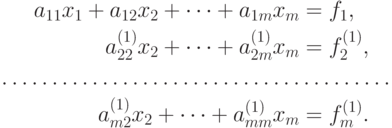
$\begin{aligned} a_{11}{x_1} + a_{12}{x_2} + \dots + a_{1m}{x_m} &= {f_1}, \\ a_{22}^{(1)}{x_2} + \dots + a_{2m}^{(1)}{x_m} &= f_2^{(1)}, \\ \dots\dots\dots\dots\dots\dots\dots\dots\dots\dots & \dots\dots\dots \\ a_{m2}^{(1)}{x_2} + \dots + a_{mm}^{(1)}{x_m} &= f_m^{(1)}. \end{aligned}$

где

$a_{ij}^{(1)} = {a_{ij}} - \frac{a_{i1}a_{1j}}{a_{11}}, \quad f_i^{(1)} = f_i - \frac{a_{i1}f_1}{a_{11}}, \quad i,j = 2,3, \dots, m.$

Аналогичным образом из полученной системы исключим x_2 . Последовательно, исключая все неизвестные, получим систему треугольного вида

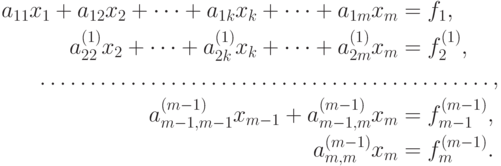
$\begin{aligned} {a_{11}}{x_1} + {a_{12}}{x_2} + \dots + {a_{1k}}{x_k} + \dots +{a_{1m}}{x_m} &= f_1, \\ a_{22}^{(1)}{x_2} + \dots + a_{2k}^{(1)}{x_k} + \dots + a_{2m}^{(1)}{x_m} &= f_2^{(1)}, \\ \dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots &\dots\dots\dots, \\ a_{m - 1,m - 1}^{(m - 1)}{x_{m - 1}} + a_{m - 1,m}^{(m - 1)}{x_m} &= f_{m - 1}^{(m - 1)},\\ a_{m,m}^{(m - 1)}{x_m} &= f_m^{(m - 1)}.\\ \end{aligned}$

Описанная процедура называется прямым ходом метода Гаусса. Заметим, что ее выполнение было возможно при условии, что все $a_{i,i}^{(l)},\ l = 1,2,\dots ,m-1$ не равны нулю. Выполняя последовательные подстановки в последней системе, (начиная с последнего уравнения) можно получить все значения неизвестных.

${x_m} &= \frac{f_m^{(m - 1)}}{a_{m,m}^{(m - 1)}},\\ {x_i} &= \frac{1}{a_{i,i}^{(i - 1)}}(f_i^{(i - 1)} - \sum\limits_{j = i - 1}^m{a_{ij}^{(i - 1)}{x_j})} .$

Эта процедура получила название обратный ход метода Гаусса.

Метод Гаусса может быть легко реализован на компьютере. При выполнении вычислений, как правило, промежуточные значения матрицы A не представляют интереса. Поэтому численная реализация метода сводится к преобразованию элементов массива размерности $m \times (m+1)$ , где m + 1 -й столбец содержит элементы правой части системы.

Для контроля ошибки реализации метода используются, так называемые, контрольные суммы. Схема контроля основывается на следующем очевидном положении. Увеличение значения всех неизвестных на единицу равносильно замене данной системы контрольной системой, в которой свободные члены равны суммам всех коэффициентов соответствующей строки. Создадим дополнительный столбец, хранящий сумму элементов матрицы по строкам. На каждом шаге реализации прямого хода метода Гаусса будем выполнять преобразования и над элементами этого столбца, и сравнивать их значение с суммой по строке преобразованной матрицы. В случае не совпадения значений счет прерывается.

Один из основных недостатков метода Гаусса связан с тем, что при его реализации накапливается вычислительная погрешность.

Для систем порядка m число действий умножения и деления близко $\cfrac{m^3}{3}$ и быстро растет с величиной .

Для того, чтобы уменьшить рост вычислительной погрешности применяются различные модификации метода Гаусса. Например, метод Гаусса с выбором главного элемента по столбцам, в этом случае на каждом этапе прямого хода строки матрицы переставляются таким образом, чтобы диагональный угловой элемент был максимальным. При исключении соответствующего неизвестного из других строк деление будет производиться на наибольший из возможных коэффициентов и, следовательно, относительная погрешность будет наименьшей.

Пример реализации метода Гаусса в Maxima приведен в функции ниже (применен метод без выбора главного элемента):

(%i1)	gauss(a0,b0,n):=block([a,b,i,j,k,d],
	a:copymatrix (a0), b:copymatrix(b0), x:copymatrix(b0),
	for i:1 thru n-1 do
	(
		for k:i+1 thru n do
		(
			d:a[k,i]/a[i,i],
			for j:i+1 thru n do (a[k,j]:a[k,j]-a[i,j]*d),
			b[k,1]:b[k,1]-b[i,1]*d
		)
	),
	for i:n thru 1 step -1 do
	(
		for j:i+1 thru n do (
			b[i,1]:b[i,1]-a[i,j]*x[j,1]),
		x[i,1]:b[i,1]/a[i,i]
	),
	x)$

Пример обращения к функции, реализующей метод Гаусса:

(%i2)	aa:matrix([3,1,1],[1,3,1],[1,1,3]); bb:matrix([6],[6],[8]);
	zz:gauss(aa,bb,3);

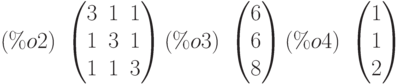
$(\%o2)\ \begin{pmatrix}3 & 1 & 1\cr 1 & 3 & 1\cr 1 & 1 & 3\end{pmatrix} (\%o3)\ \begin{pmatrix}6\cr 6\cr 8\end{pmatrix} (\%o4)\ \begin{pmatrix}1\cr 1\cr 2\end{pmatrix}$

Проверка вычислений показывает, что перемножение матрицы на вектор решения дает вектор, совпадающий с вектором правых частей .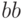

(%i5)	aa.zz;

$(\%o5)\ \begin{pmatrix}6.0\cr 6.0\cr 8.0\end{pmatrix}$

Существует метод Гаусса с выбором главного элемента по всей матрице. В этом случае переставляются не только строки, но и столбцы. Использование модификаций метода Гаусса приводит к усложнению алгоритма увеличению числа операций и соответственно к росту времени счета.

Выполняемые в методе Гаусса преобразования прямого хода, приведшие матрицу системы к треугольному виду позволяют вычислить определитель матрицы

$\det A = \left| {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}& \ldots &{{a_{1m}}} \\ 0&{a_{22}^{(1)}}& \ldots &{a_{2m}^{(1)}} \\ \ldots & \ldots & \ldots & \ldots \\ 0&0& \ldots &{a_{m,m}^{(m - 1)}} \end{array}} \right| = {a_{11}} \cdot a_{22}^{(1)} \ldots a_{m,m}^{(m - 1)}$

Метод Гаусса позволяет найти и обратную матрицу. Для этого необходимо решить матричное уравнение

$A \cdot X = E,$

где

– единичная матрица. Его решение сводится к решению

систем

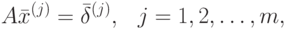
$A{\bar x^{(j)}} = {\bar \delta ^{(j)}},\begin{array}{*{20}{c}} {}&{j = 1,2,\dots,m,}$

у вектора ${\bar \delta ^{(j)}}\ j$ –я компонента равна единице, а остальные компоненты равны нулю.

8.3.3 Метод квадратного корня

Метод квадратного корня основан на разложении матрицы в произведение

$A=S^{T}S,$

где

— верхняя треугольная матрица с положительными элементами на главной диагонали, S^T

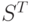— транспонированная к ней матрица.

Пусть — матрица размером $m\times m$ . Тогда

${\left( {{S^T}S} \right)_{ij}} = \sum\limits_{k = 1}^m {s_{ik}^Ts_{kj}^{}}$

( 8.2)

Из условия (8.2) получаются уравнения

$\sum\limits_{k = 1}^m {s_{ik}^T{s_{kj}} = {a_{ij}}, \qquad i,j = 1,2,\dots..,m}$

( 8.3)

Так как матрица симметричная, не ограничивая общности, можно считать, что в системе (8.3) выполняется неравенство $i\le j$ . Тогда (8.3) можно переписать в виде

$\begin{align*} \sum\limits_{k = 1}^{i - 1} s_{ik}^T s_{kj} + s_{ii} s_{ij} + \sum\limits_{k = i + 1}^m s_{ik}^T s_{kj} = a_{ij} \\ s_{ii} s_{ij} + \sum\limits_{k = 1}^{i - 1} s_{ik}^T s_{kj} = a_{ij}, \quad i \leqslant j. \end{align*}$

В частности, при 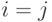i = j получится

$\begin{align*} \left| s_{ii} \right|^2 = a_{ii} - \sum\limits_{k = 1}^{i - 1} \left| s_{ki} \right|^2 \\ s_{ii} = \left( \left| a_{ii} - \sum\limits_{k = 1}^{i - 1} \left| s_{ki} \right|^2 \right| \right)^{1/2} \end{align*}$

Далее, при 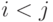i < j получим

$s_{ij} = \frac{ a_{ij} - \sum\limits_{k = 1}^{i - 1} s_{ik}^T s_{kj} } {s_{ii}}$

По приведённым формулам находятся рекуррентно все ненулевые элементы матрицы .

Обратный ход метода квадратного корня состоит в последовательном решении двух систем уравнений с треугольными матрицами.

$\begin{align*} S^{T}y = f,\\ Sx = y. \end{align*}$

Решения этих систем находятся по рекуррентным формулам:

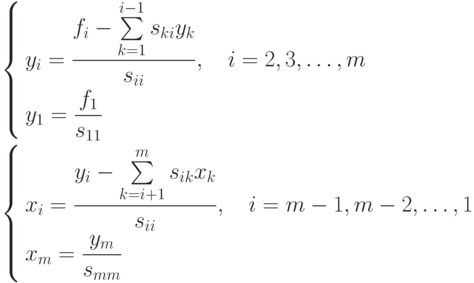
$\begin{aligned} &\left\{ \begin{aligned} & {y_i} = \frac{f_i - \sum\limits_{k = 1}^{i - 1} s_{ki}{y_k}}{s_{ii}}, \quad i = 2,3, \dots ,m \hfill \\ & {y_1} = \frac{f_1}{s_{11}} \end{aligned} \right. \\ &\left\{ \begin{aligned} & {x_i} = \frac{y_i - \sum\limits_{k =i+1}^{m} s_{ik}{x_k}}{s_{ii}}, \quad i = m-1,m-2, \dots ,1 \hfill \\ & {x_m} = \frac{y_m}{s_{mm}} \end{aligned} \right. \end{aligned}$

Всего метод квадратного корня при факторизации A = S^TS требует примерно $\cfrac{m^3}{3}$ операций умножения и деления и m операций извлечения квадратного корня.

Пример функции, реализующей метод квадратного корня:

(%i1)	holetsk(a0,b0):=block([L,Lt,x,y,i,j,k,n],
	n:length(a0), L:zeromatrix(n,n),
	for i:1 thru n do (
		for j:1 thru i-1 do (
		s:0,
		for k:1 thru j-1 do (s:s+L[i,k]*L[j,k]),
		L[i,j]:1/L[j,j]*(a0[i,j]-s)
		),
		s:0,
		for k:1 thru i-1 do (s:s+L[i,k]^2),
		L[i,i]:sqrt(a0[i,i]-s)
		),Lt:transpose(L),
	y:zeromatrix(n,1), x:zeromatrix(n,1),
	for i:1 thru n do (
		s:0,
		for k:1 thru i-1 do (s:s+L[i,k]*y[k,1]),
			y[i,1]:(b0[i,1]-s)/L[i,i]
	),
	for i:n thru 1 step -1 do (
		s:0,
		for k:n thru i+1 step -1 do (s:s+Lt[i,k]*x[k,1]),
		x[i,1]:(y[i,1]-s)/Lt[i,i]
	),x
	)$

Тест данной функции (решение системы Ax = B, B — матрица $n\times 1,\ A$ — квадратная симметричная матрица $n \times n$ , результат решения — вектор $n \times 1$ ):

(%i2)	A:matrix([4,1,1],[1,4,1],[1,1,4])$ B:matrix([1],[1],[1])$

Результаты вычислений:

(%i4)	x:holetsk(A,B);

$(\%o4)\ \begin{pmatrix}\frac{1}{6}\cr \frac{1}{6}\cr \frac{1}{6}\end{pmatrix}$

Проверка:

(%i5)	A.x;

$(\%o5) \begin{pmatrix}1\cr 1\cr 1\end{pmatrix}$

8.3.4 Корректность постановки задачи и понятие обусловленности

При использовании численных методов для решения тех или иных математических задач необходимо различать свойства самой задачи и свойства вычислительного алгоритма, предназначенного для ее решения.

Говорят, что задача поставлена корректно, если решение существует и единственно и если оно непрерывно зависит от входных данных. Последнее свойство называется также устойчивостью относительно входных данных.

Корректность исходной математической задачи еще не гарантирует хороших свойств численного метода ее решений и требует специального исследования.

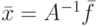Известно, что решение задачи (8.1) существует тогда и только тогда, когда $\det A \ne 0$ . В этом случае можно определить обратную матрицу ${A^{ - 1}}$ и решение записать в виде $\bar x = {A^{ - 1}}\bar f$ .

Исследование устойчивость задачи (8.1) сводится к исследованию зависимости ее решения от правых частей 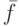$\bar f$ и элементов 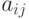$a_{ij}$ матрицы . Для того чтобы можно было говорить о непрерывной зависимости вектора решений от некоторых параметров, необходимо на множестве -мерных векторов принадлежащих линейному пространству $\mathbb H$ , ввести метрику.

В линейной алгебре предлагается определение множества метрик ${l_p}$ — норма $\left\|{\bar x} \right\|_p = \left( \sum\limits_{i = 1}^m \left| x_i \right|^p \right)^{1/p}$ из которого легко получить наиболее часто используемые метрики

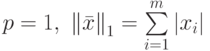при $p=1,\ \left\| {\bar x} \right\|_1 = \sum\limits_{i = 1}^m \left| {x_i}\right|$ ,
при
$p = 2,\ {\left\| {\bar x} \right\|_2} = \left( \sum\limits_{i = 1}^m {\left| {x_i} \right|^2} \right)^{1/2}$
,
при
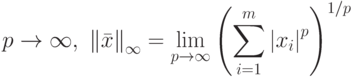
$p \to \infty,\ {\left\| {\bar x} \right\|_\infty } = \mathop {\lim} \limits_{p \to \infty } \left( \sum\limits_{i = 1}^m \left| {{x_i}} \right|^p \right)^{1/p}$
.

Подчиненные нормы матриц определяемые как 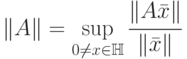$\left\| A \right\| = \mathop {\sup }\limits_{0 \ne x \in \mathbb H} \cfrac{{\left\| {A\bar x} \right\|}}{{\left\| {\bar x} \right\|}}$ , соответственно записываются в следующем виде:

$\begin{align*} {\left\| A \right\|_1} = \mathop {\max }\limits_{1 \leqslant j \leqslant m} \sum\limits_{i = 1}^m {\left| {{a_{ij}}} \right|} ,\\ {\left\| A \right\|_\infty } = \mathop {\max }\limits_{1 \leqslant i \leqslant m} \sum\limits_{i = 1}^m {\left| {{a_{ij}}} \right|} ,\\ {\left\| A \right\|_2} = \sqrt {\rho ({A^T}A)} = \sqrt {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {a_{ij}^2} } }. \end{align*}$

Обычно рассматривают два вида устойчивости решения системы (8.1):

по правым частям;
по коэффициентам системы (8.1) и по правым частям.

Наряду с исходной системой (8.1) рассмотрим систему с "возмущенными" правыми частями

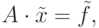
$A \cdot \tilde x = \tilde f,$

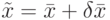где $\tilde f = \bar f + \delta \bar f$ возмущенная правая часть системы, а $\tilde x = \bar x + \delta \bar x$ возмущенное решение.

Можно получить оценку, выражающую зависимость относительной погрешности решения от относительной погрешности правых частей

$\frac{{\left\| {\delta \bar x} \right\|}}{{\left\| {\bar x} \right\|}} \leqslant {M_A}\frac{{\left\| {\delta \bar f} \right\|}}{{\left\| {\bar f} \right\|}},$

где ${M_A} = \left\| A \right\| \cdot \left\| {{A^{ - 1}}} \right\|$ — число обусловленности матрицы

(в современной литературе это число обозначают как cond(A)

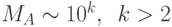). Если число обусловленности велико ( ${M_A}\sim{10^k}, \,\,\,k > 2$ ), то говорят, что матрица

плохо обусловлена. В этом случае малые возмущения правых частей системы (8.1), вызванные либо неточностью задания исходных данных, либо вызванные погрешностями вычисления существенно влияют на решение системы.

Если возмущение внесено в матрицу , то для относительных возмущений решения имеет место следующая оценка:

$\frac{\left\| {\delta \bar x} \right\|} {\left\| {\bar x} \right\|} \leqslant \frac{M_A} {{1 - {M_A}\cfrac{{\left\| {\delta A} \right\|}}{{\left\|A \right\|}}}} \left( \frac{\left\| {\delta A} \right\|}{{\left\| A \right\|}} + \cfrac{\left\| {\delta \bar f} \right\|} {\left\|{\bar f}\right\|} \right).$

В Maxima матричные нормы вычисляются посредством функции mat_norm . Синтаксис вызова: mat_norm(M,type) , где — матрица, type — тип нормы, type может быть равен 1 (норма ${\left\| A \right\|_1}$ ), inf (норма ${\left\| A \right\|_\infty }$ ), frobenius (норма $\left\| A \right\|_2$ ).

Пример вычисления указанных видов нормы в Maxima:

(%i1)	A:matrix([1,2,3],[4,5,6],[7,8,9]);

$(\%o1)\ \begin{pmatrix}1 & 2 & 3\cr 4 & 5 & 6\cr 7 & 8 & 9\end{pmatrix}$

(%i2)	mat_norm(A,1);

$(\%o2)\ 18$

(%i3)	mat_norm(A,inf);

$(\%o3)\ 24$

(%i4)	mat_norm(A,frobenius);

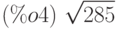
$(\%o4)\ \sqrt{285}$

Вычислим число обусловленности для плохо и хорошо обусловленных матриц:

(%i1)	A:matrix([1,1],[0.99,1]);

$(\%o1)\ \begin{pmatrix}1 & 1\cr 0.99 & 1\end{pmatrix}$

(%i2)	nrA:mat_norm(A,frobenius);

$(\%o2)\ 1.995018796903929$

(%i3)	A1:invert(A);

$(\%o3)\ \begin{pmatrix}99.99999999999992 & -99.99999999999992\cr -98.99999999999992 & 99.99999999999992\end{pmatrix}$

(%i4)	nrA1:mat_norm(A1,frobenius);

$(\%o4)\ 199.5018796903927$

(%i5)	MA:nrA*nrA1;

$(\%o5)\ 398.0099999999997$

Таким образом, для плохо обусловленной матрицы число обусловленности достигает почти 400.

Аналогичным путём (с использованием нормы Фробениуса) для матрицы $B=\left[ \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right]$ число обусловленности составило MB = 2 .

8.3.5 О вычислительных затратах

Один из важных факторов предопределяющих выбор того или иного метода при решении конкретных задач, является вычислительная эффективность метода. Учитывая, что операция сложения выполняется намного быстрее, чем операция умножения и деления, обычно ограничиваются подсчетом последних. Для решения СЛАУ методом Гаусса без выбора главного элемента требуется 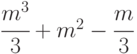$\cfrac{{{m^3}}}{3} + {m^2} - \cfrac{m}{3}$ умножений и делений, решение СЛАУ методом квадратного корня требует $\cfrac{{{m^3}}}{6} + \cfrac{3m^2}{2} +\cfrac{m}{3}$ и операций извлечения корней. При больших значениях размерности , можно сказать, что вычислительные затраты на операции умножения и деления в методе Гаусса составляют величину $O\left( {\cfrac{{{m^3}}}{3}}\right)$ , в методе квадратных корней $O\left( {\cfrac{{{m^3}}}{6}} \right)$ .

Дальше >>

Авторизоваться

Компьютерная математика с Maxima

Реализация некоторых численных методов