Задачи высшей математики с Maxima
3.1 Операции с комплексными числами
3.1.1 Представление комплексных чисел
Значение целой положительной степени комплексного аргумента проще всего вычислять в тригонометрической форме. Если  ) (здесь
) (здесь  — модуль комплексного числа,
— модуль комплексного числа,  — его аргумент), то для любого целого положительного числа
— его аргумент), то для любого целого положительного числа  имеет место формула:
имеет место формула:  .
.
Корнем  -й степени из комплексного числа
-й степени из комплексного числа 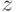 называется число
называется число ![w = \sqrt[n]{z}](/sites/default/files/tex_cache/894090dbb70889f72228ffb87a8475f8.png) такое, что
такое, что  . Для любого комплексного числа
. Для любого комплексного числа 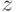 существует
существует  комплексных чисел
комплексных чисел  таких, что
таких, что  . Значение корня, т.е. значение функции
. Значение корня, т.е. значение функции ![f(z) = \sqrt[n]{z}](/sites/default/files/tex_cache/a82a7533089a1b6a736f836783ad7ec6.png) также удобно вычислять в тригонометрической форме. Если
также удобно вычислять в тригонометрической форме. Если  , то для любого целого положительного числа
, то для любого целого положительного числа  имеет место формула:
имеет место формула: ![f(z) = \sqrt[n]{z} = \sqrt[n]{r\left(\cos \varphi + i \sin \varphi \right) } = \sqrt[n]{r}\left( \cos \frac{\varphi+2k\pi}{n} + \sin \frac{\varphi+2k\pi}{n} \right)](/sites/default/files/tex_cache/5ffce7400364d143436922eb0c2e12fe.png) , т.е. функция
, т.е. функция ![f(z) = \sqrt[n]{z}](/sites/default/files/tex_cache/a82a7533089a1b6a736f836783ad7ec6.png) является многозначной функцией — каждому значению аргумента отвечает
является многозначной функцией — каждому значению аргумента отвечает  различных значений корня.
различных значений корня.
Если, то значения функции
вычисляются по формуле
.
Логарифмом комплексного числа 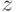 называется такое число
называется такое число  , что
, что  . Значения логарифмической функции
. Значения логарифмической функции  вычисляются по формуле
вычисляются по формуле  Величину
Величину  называют главным значением логарифма. Функция
называют главным значением логарифма. Функция  является многозначной функцией — каждому значению аргумента отвечает бесконечное множество различных значений логарифма.
является многозначной функцией — каждому значению аргумента отвечает бесконечное множество различных значений логарифма.
Комплексное выражение определено в Maxima посредством сложения действительной части выражения и произведения  (мнимой единицы) и мнимой части (т.е. в алгебраической форме). Например, корни из уравнения
(мнимой единицы) и мнимой части (т.е. в алгебраической форме). Например, корни из уравнения  равны
равны 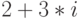 и
и 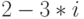 . Решение в Maxima:
. Решение в Maxima:
(%i1) eq:x^2-4*x+13=0;

(%i2) solve(eq,x);
![[x=2-3\,i,x=3\,i+2]\leqno{ (\%o2) }](/sites/default/files/tex_cache/c5bcd273cd791621a47b001d0249e72a.png)
(%i3) x1:%o2[1]$ x2:%o2[2];

(%i4) print(x1,x2);

Более сложный пример вычисления корней алгебраического уравнения  -й степени:
-й степени:
(%i1) solve(x^3=1,x);
![[x=\frac{\sqrt{3}\,i-1}{2},x=-\frac{\sqrt{3}\,i+1}{2},x=1]\leqno{ (\%o1) }](/sites/default/files/tex_cache/8e5fe43d23d03605a0ce0fd0e4b6cdd4.png)
(%i2) solve(x^5=1,x);
![[x={e}^{\frac{2\,i\,\pi }{5}},x={e}^{\frac{4\,i\,\pi
}{5}},x={e}^{-\frac{4\,i\,\pi }{5}},x={e}^{-\frac{2\,i\,\pi }{5}},x=1]\leqno{
(\%o2) }](/sites/default/files/tex_cache/0e0872b848ef414590aa52a9c4182bb8.png)
Количество корней, возвращаемое Maxima, соответствует основной теореме алгебры (уравнение третьей степени имеет три корня, пятой — пять и т.д.).
Преобразование комплексных выражений может осуществляться функциями для работы с алгебраическими выражениями ( и др.), но предусмотрен и ряд специфических функций, рассчитанных на операции именно с комплексными числами.
и др.), но предусмотрен и ряд специфических функций, рассчитанных на операции именно с комплексными числами.
3.1.2 Функции для работы с комплексными числами
Упрощение частных, корней, и других функций комплексных выражений может обычно достигаться при использовании функций  .
.
Вычисление модуля комплексного числа осуществляется функцией 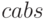 . Аргумент комплексного выражения вычисляется при помощи функции
. Аргумент комплексного выражения вычисляется при помощи функции  . Комплексный аргумент —
. Комплексный аргумент —  в пределах
в пределах ![[-\pi, \pi]](/sites/default/files/tex_cache/86f9a3a2cc344b78b146c202b2226bae.png) таким образом, что
таким образом, что  , где
, где  — модуль комплексного числа
— модуль комплексного числа 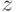 . Следует учитывать, что
. Следует учитывать, что  — вычислительная функция, не предназначенная для упрощения комплексных выражений. (в некоторых случаях удобно использовать опцию
— вычислительная функция, не предназначенная для упрощения комплексных выражений. (в некоторых случаях удобно использовать опцию  , установка которой заставляет представлять результаты в формате с плавающей точкой — см. пример ниже).
, установка которой заставляет представлять результаты в формате с плавающей точкой — см. пример ниже).
Пример:
(%i1) carg (1);

(%i2) carg (1 + %i);

(%i3) carg (exp (%i)),numer;

(%i4) carg (exp (%pi * %i));

(%i5) carg (exp (3/2 * %pi * %i));

Для преобразования комплексных выражений используют также функцию  . Управление её работой осуществляется флагом
. Управление её работой осуществляется флагом  .
.
Когда переменная  установлена (
установлена ( ), комплексные показательные функции преобразованы в эквивалентные выражения в терминах тригонометрических функций:
), комплексные показательные функции преобразованы в эквивалентные выражения в терминах тригонометрических функций:  упрощает к виду
упрощает к виду 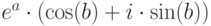 , если выражение
, если выражение  не содержит
не содержит  . Значение по умолчанию
. Значение по умолчанию  .
.
Кроме того, преобразование различных форм комплексных чисел осуществляется функцией  , которая преобразует тригонометрические и гиперболические функции в экспоненциальную форму. Флаги
, которая преобразует тригонометрические и гиперболические функции в экспоненциальную форму. Флаги  и
и  не могут оба быть установлены в
не могут оба быть установлены в  одновременно.
одновременно.
Пример:
(%i1) demoivre:true;

(%i2) demoivre (exp (3+3/2 * %pi * %i));

(%i3) demoivre (exp (%pi+3/2 * %pi * %i));

Комплексно-сопряжённые выражения вычисляются при помощи функции 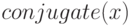 .
.
Пример:
(%i1) declare ([aa, bb], real, cc, complex, ii, imaginary);

(%i2) conjugate (aa + bb*%i);

(%i3) conjugate (ii);

Как видно из примера, функция  позволяет объявить тип выражений: действительные, комплексные и чисто мнимые (
позволяет объявить тип выражений: действительные, комплексные и чисто мнимые ( ).
).
Функция 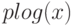 представляет основную ветвь комплексного логарифма, соответствующую
представляет основную ветвь комплексного логарифма, соответствующую  , например:
, например:
(%i1) a:1+%i;

(%i2) plog(a);

Функция  возвращает выражение
возвращает выражение  , эквивалентное
, эквивалентное  (параметры
(параметры  и
и  действительны).
действительны).
Преобразование комплексного выражения к алгебраической форме осуществляется функцией  .
.
Пример:
(%i1) a:1+%i;

(%i2) polarform(a);

(%i3) rectform(%);

Функция  ) вычисляет остаток в комплексной плоскости для выражения
) вычисляет остаток в комплексной плоскости для выражения  , когда переменная z принимает значение
, когда переменная z принимает значение  . Остаток — коэффициент при
. Остаток — коэффициент при  ряда Лорана для
ряда Лорана для  .
.
Пример:
(%i1) residue (s/(s**2+a**2), s, a*%i);

(%i2) residue (sin(a*x)/x**4, x, 0);

