Информационно-логические основы ЭВМ
Системы счисления
Системой счисления называется способ изображения чисел с помощью ограниченного набора символов, имеющих определенные количественные значения. Систему счисления образует совокупность правил и приемов представления чисел с помощью набора знаков (цифр).
Различают позиционные и непозиционные системы счисления. В позиционных системах каждая цифра числа имеет определенный вес, который зависит от позиции цифры в последовательности, изображающей число. Позиция цифры называется разрядом. В позиционной системе счисления любое число можно представить в виде:
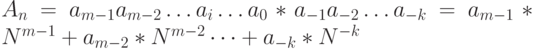
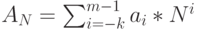 |
( 14.1) |
где 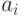 -
-  -я цифра числа;
-я цифра числа;
 - количество цифр в дробной части числа;
- количество цифр в дробной части числа;
 - количество цифр в целой части числа;
- количество цифр в целой части числа;
 - основание системы счисления.
- основание системы счисления.
Основание системы счисления  показывает, во сколько раз "вес"
показывает, во сколько раз "вес"  -го разряда больше (
-го разряда больше ( ) разряда. Целая часть числа отделяется от дробной части точкой (запятой).
) разряда. Целая часть числа отделяется от дробной части точкой (запятой).
Пример 14.1.  .
.
В соответствии с формулой (14.1) это число формируется из цифр с весами разрядов:
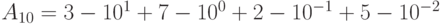
Теоретически наиболее экономичной системой счисления для представления значения числа цифрами является система с основанием  , находящимся между числами 2 и 3.
, находящимся между числами 2 и 3.
Во всех современных ЭВМ для представления числовой информации применяется двоичная система счисления. Это обусловлено:
- более простой реализацией алгоритмов выполнения арифметических и логических операций;
- более надежной физической реализацией основных функций, так как они имеют всего два состояния (0 и 1);
- экономичностью аппаратной реализации всех схем ЭВМ.
При  число различных цифр, используемых для записи чисел, ограничено множеством из двух цифр (нуль и единица). Кроме двоичной системы счисления, широкое распространение получили и производные системы:
число различных цифр, используемых для записи чисел, ограничено множеством из двух цифр (нуль и единица). Кроме двоичной системы счисления, широкое распространение получили и производные системы:
- двоичная -
 ;
; - десятичная, точнее двоично-десятичное представление десятичных чисел -
 ;
; - шестнадцатеричная -
 . Здесь шестнадцатеричная цифра
. Здесь шестнадцатеричная цифра  обозначает число 10,
обозначает число 10,  - число 11, ...,
- число 11, ...,  - число 15;
- число 15; - восьмеричная (от слова восьмерик) -
 . Она широко используется во многих специализированных ЭВМ.
. Она широко используется во многих специализированных ЭВМ.
Восьмеричная и шестнадцатеричная системы счисления являются производными от двоичной, так как  и
и  . Они применяются в основном для более компактного изображения двоичной информации, так как запись значения чисел производится существенно меньшим числом знаков
. Они применяются в основном для более компактного изображения двоичной информации, так как запись значения чисел производится существенно меньшим числом знаков
Пример 14.2. Число  в двоичной, восьмеричной и шестнадцатеричной системах счисления имеют следующее представление:
в двоичной, восьмеричной и шестнадцатеричной системах счисления имеют следующее представление:
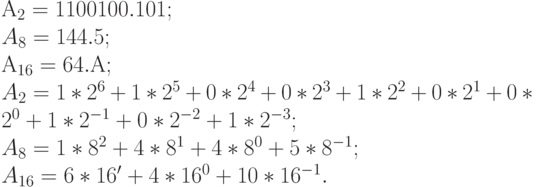
В табл. 14.1 приведено сравнительное представление чисел в различных системах счисления: десятичной (10 с/с), двоичной (2 с/с), восьмеричной (8 с/с) и шестнадцатеричной (16 с/с).
По данным этой таблицы можно выявить целый ряд закономерностей:
- нуль и единица имеют единственное и одинаковое представление в любых системах счисления;
- основание системы счисления в любой системе имеет представление 10;
-
незначащие нули слева от целой части и справа от дробной части числа не изменяют значений чисел;
Таблица 14.1. Представление чисел в различных системах счисления 10c/c 2c/c 8c/c 16c/c 10c/c 2c/c 8c/c 16c/c Целые числа Целые числа 0 00000 0 0 10 01010 12 A 1 00001 1 1 11 01011 13 B 2 00010 2 2 12 01100 14 C 3 00011 3 3 13 -1101 15 D 4 00100 4 4 14 01110 16 E 5 00101 5 5 15 01111 17 F 6 00110 6 6 16 10000 20 10 7 00111 7 7 17 10001 21 11 8 01000 10 8 18 10010 22 12 9 01001 11 9 и.т.д. Дробные числа Дробные числа 0.5 0.1 0.4 0.8 0.0625 0.0001 0.04 0.1 0.25 0.01 0.2 0.4 0.03125 0.00001 0.02 0.08 0.125 0.001 0.1 0.2 и т.д. - представление чисел в различных системах счисления допускает однозначное их преобразование из одной системы в другую.
В ЭВМ перевод из одной системы в другую осуществляется автоматически, по специальным программам. Правила перевода целых и дробных чисел отличаются.
Необходимо сделать несколько замечаний. В общем случае перевод любого числа с дробью из одной системы счисления в другую может привести к появлению иррациональных чисел, имеющих бесконечное количество разрядов в дробной части чисел. Естественно, что любое техническое устройство, например компьютер, может оперировать только с конечным числом цифр, являющихся старшими, наиболее значимыми разрядами.
Игнорирование, отбрасывание младших разрядов чисел приводит к их округлению. При этом разница между округляемым и полученным числами называется ошибкой округления. Следует учитывать, что округление результатов вычислений по любому неслучайному правилу приводит к ошибкам с ненулевым смещением [83].
Перевод целых чисел
Целое число с основанием  переводится в систему счисления с основанием
переводится в систему счисления с основанием 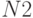 путем последовательного деления числа
путем последовательного деления числа 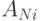 на основание
на основание 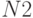 , записанного в виде числа с основанием
, записанного в виде числа с основанием  , до получения остатка. Полученное частное следует вновь делить на основание
, до получения остатка. Полученное частное следует вновь делить на основание 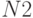 , и этот процесс надо повторять до тех пор, пока частное не станет меньше делителя.
, и этот процесс надо повторять до тех пор, пока частное не станет меньше делителя.
Полученные остатки от деления и последнее частное записываются в порядке, обратном полученному при делении. Сформированное число и будет являться числом с основанием 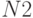 .
.
Пример 14.3. 
Перевод дробных чисел
Дробное число с основанием  переводится в систему счисления с основанием
переводится в систему счисления с основанием 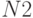 путем последовательного умножения <<Eqn010.eps>> на основание
путем последовательного умножения <<Eqn010.eps>> на основание 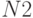 , записанное в виде числа с основанием
, записанное в виде числа с основанием  . При каждом умножении целая часть произведения берется в виде очередной цифры соответствующего разряда, а оставшаяся дробная часть принимается за новое множимое. Число умножений определяет разрядность полученного результата, представляющего число
. При каждом умножении целая часть произведения берется в виде очередной цифры соответствующего разряда, а оставшаяся дробная часть принимается за новое множимое. Число умножений определяет разрядность полученного результата, представляющего число 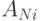 в системе счисления
в системе счисления 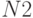 .
.
Пример 14.4. 
Так как двоичная, восьмеричная и шестнадцатеричная системы связаны через степени числа 2, то преобразования между ними можно вы-полнять другим, более простым способом. Для перевода из шестнадцатеричной (восьмеричной) системы счисления в двоичную достаточно двоичным кодом записать шестнадцатеричные коды цифр тетрадами (по 4 двоичных разряда) и триадами (по 3 двоичных разряда) - для восьмеричных цифр. Обратный перевод из двоичного кода производится в обратном порядке: двоичное число разбивается влево и вправо от границы целой и дробной частей на тетрады - для последующей записи цифр в шестнадцатеричном представлении, на триады - для записи их значений восьмеричными цифрами.
Арифметические основы ЭВМ
Представление числовой информации в компьютере
В компьютерах используются три вида чисел: с фиксированной точкой (запятой), с плавающей точкой (запятой) и двоично-десятичное представление. Точка (запятая) - это подразумеваемая граница целой и дробной частей числа, разряды  и
и формулы (4.1).
формулы (4.1).
Все современные компьютеры имеют центральный процессор или центральное процессорное устройство - CPU (Central Processing Unit), предназначенное для обработки чисел с фиксированной точкой. Одной из важнейших его характеристик является разрядность  - количество двоичных разрядов, представляющих значение числа. Основным достоинством CPU служит простота алгоритмов выполнения операций и, соответственно, высокая скорость операций.
- количество двоичных разрядов, представляющих значение числа. Основным достоинством CPU служит простота алгоритмов выполнения операций и, соответственно, высокая скорость операций.
У чисел с фиксированной точкой в двоичном формате предполагается строго определенное место точки (запятой). Обычно это место определяется или перед первой цифрой числа, или после последней цифры числа. Если точка фиксируется перед первой значащей цифрой, то это означает, что число по модулю меньше единицы. Диапазон изменения значений чисел определяется неравенством:
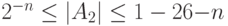
Если точка фиксируется после последней цифры, то это означает, что  -разрядные двоичные числа являются целыми. Диапазон изменения их значений составляет:
-разрядные двоичные числа являются целыми. Диапазон изменения их значений составляет:
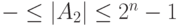
Перед самым старшим из возможных цифровых разрядов двоичного числа фиксируется его знак. Положительные числа имеют нулевое значение знакового разряда, отрицательные - единичные. Каждая цифра двоичного числа  занимает один бит соответствующего
занимает один бит соответствующего  -разрядного формата.
-разрядного формата.
Существенным недостатком представления чисел с фиксированной точкой служит тот факт, что аппроксимация малых чисел связана с большой относительной ошибкой. Для чисел же, приближающихся по величине к максимально возможным ( ), относительная ошибка уменьшается. Абсолютная же ошибка представления чисел с фиксированной точкой всегда лежит в одних и тех же пределах независимо от величины чисел.
), относительная ошибка уменьшается. Абсолютная же ошибка представления чисел с фиксированной точкой всегда лежит в одних и тех же пределах независимо от величины чисел.
Другой формой представления чисел является представление их в виде чисел с плавающей точкой (запятой). Представление чисел с плавающей точкой необходимо использовать, когда обрабатываемые числа имеют очень большой диапазон изменения. Эта ситуация типична для научно-технических расчетов (тригонометрические, экспоненты, логарифмы). Поэтому все современные микропроцессоры в качестве дополнения к CPU имеют математические сопроцессоры. Их обычно называют блоками или устройствами с плавающей точкой - FPU (Floating Point Unit), или числовым расширением процессора - NPX (Numeric Processor eXtension). Сочетание параллельно работающих CPU и FPU позволяет добиться большей скорости и большей точности вычислений.
Числа с плавающей точкой представляются в виде мантиссы  и порядка
и порядка  , иногда это представление называют полулогарифмической формой числа. Например, число
, иногда это представление называют полулогарифмической формой числа. Например, число  можно представить в виде
можно представить в виде  , при этом
, при этом  , основание системы счисления подразумевается фиксированным и равным десяти. Для двоичных чисел
, основание системы счисления подразумевается фиксированным и равным десяти. Для двоичных чисел  в этом представлении также формируется
в этом представлении также формируется  и порядок
и порядок  при основании системы счисления, равном двум.
при основании системы счисления, равном двум.

что соответствует записи
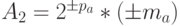
Детализация двоичного представления чисел с плавающей точкой и двоично-десятичная форма чисел подробно освещены в [88]. Поскольку их представление и обработка базируются на двоичной арифметике, рассмотрим правила сложения двоичных цифр.
Все современные ЭВМ имеют достаточно развитую систему команд, включающую десятки и сотни машинных операций. Однако выполнение любой операции основано на использовании простейших микроопераций типа сложения и сдвига. Это позволяет иметь единое арифметико-логическое устройство для выполнения любых операций, связанных с обработкой информации. Сложение двоичных цифр двух чисел  и
и  иллюстрируется табл. 14.2.
иллюстрируется табл. 14.2.
| Значения двоичных чисел А и В | Разряд суммы | Перенос в следующий разряд | ||
|---|---|---|---|---|
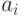 |
 |
 |
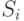 |
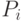 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Здесь показаны правила сложения двоичных цифр 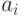 ,
,  одноименных разрядов с учетом возможных переносов из предыдущего разряда
одноименных разрядов с учетом возможных переносов из предыдущего разряда  .
.
Подобные таблицы можно было бы построить для любой другой арифметической и логической операции (вычитание, умножение и т.д.), но именно данные этой таблицы положены в основу выполнения любой операции ЭВМ. Под знак чисел отводится специальный знаковый разряд. Знак "+" кодируется двоичным нулем, а знак "-" - единицей. Действия над прямыми кодами двоичных чисел при выполнении операций создают большие трудности, связанные с необходимостью учета значений знаковых разрядов:
- во-первых, следует отдельно обрабатывать значащие разряды чисел и разряды знака;
- во-вторых, значение разряда знака влияет на алгоритм выполнения операции, например, сложение может заменяться вычитанием и наоборот.
Во всех ЭВМ без исключения все операции выполняются над числами, представленными специальными машинными кодами. Их использование позволяет обрабатывать знаковые разряды чисел так же, как и цифровые разряды, а также заменять операцию вычитания операцией сложения.
Различают прямой код (П), обратный код (ОК) и дополнительный код (ДК) двоичных чисел.


