Анализ потоков данных
Прямая и обратная задачи
Приведенное выше определение описывает так называемую прямую задачу. Она характеризуется тем, что фактически разметка before ассоциируется с входящими ребрами вершины, а разметка after - с исходящими. Таким образом, потоковая информация как бы "перемещается" сверху-вниз.
Естественным образом возникает симметричное определение, при котором разметка before ассоциируется с исходящими ребрами, а разметка after - с входящими. При этом потоковая информация распространяется снизу-вверх. Видно, что обратная задача превращается в прямую при изменении направлений всех ребер на противоположные.
Далее мы рассмотрим примеры постановки конкретных задач анализа потоков данных, используя описанный выше формализм.
Достижимые определения
Достижимые определения являются прямой задачей. Будем считать, что каждая вершина графа содержит не более одного присваивания произвольной переменной.
В качестве полурешетки потоковых фактов фиксируется множество подмножеств присваиваний с операцией объединения. Наибольшим и наименьшим элементами данной полурешетки являются соответственно множество всех присваиваний и пустое множество. Очевидно, данная полурешетка имеет конечную высоту.
В качестве потоковых функций для каждой вершины графа определим функцию, которая добавляет к своему аргументу множество всех присваиваний в данной вершине.
Наконец, начальными разметками являются разметки, сопоставляющие вершинам графа наименьшие элементы полурешетки.
Живые переменные
Живые переменные - это обратная задача. В качестве полурешетки потоковых фактов выбирается множество подмножеств переменных с операцией объединения, наибольший и наименьший элементы полурешетки очевидны, так же как и факт конечности высоты.
Для произвольной вершины v определим множество Dv как совокупность всех переменных, встречающихся в левых частях всех присваиваний в v, множество Uv как совокупность всех переменных, имеющих иные вхождения в операторы v. Определим для каждой вершины v потоковую функцию
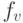
В качестве начальной разметки также избирается разметка исходного графа наименьшим элементом полурешетки.




