Анализ потоков данных
Разметки и потоковые функции
Опишем теперь общий подход к решению задачи анализа потоков данных более формально.
Зафиксируем некоторое частично упорядоченное множество "фактов" (утверждений о свойствах программы) X. Отображение 
сопоставляющее вершинам графа управления элементы X, назовем разметкой. Поточечное распространение отношений равенства и порядка вводит аналогичные отношения на множестве разметок.
Функцией перехода назовем отображение F, которое переводит одну разметку в другую. Разметку 
назовем неподвижной точкой отображения 
тогда и только тогда, когда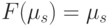 
.
Неформально говоря, разметка представляет собой некоторый набор потоковых утверждений (т.е. утверждений о свойствах потоков данных) для каждой вершины графа. Решение задачи в этом случае также может быть представлено с помощью такой разметки, а процесс решения задачи анализа потоков данных может быть описан как последовательное уточнение разметки, отталкиваясь от некоторой начальной.
Итеративный алгоритм
Основной проблемой описанного выше подхода является проблема остановки алгоритма. Действительно, в какой момент процесс уточнения разметки должен прекратиться? Очевидно, в тот момент, когда получено решение задачи анализа потоков данных. Однако поскольку решение задачи неизвестно, то и воспользоваться этим наблюдением напрямую оказывается невозможным. Поэтому для определения завершаемости алгоритма используется другой принцип - принцип достижения неподвижонй точки.
Частично-упорядоченное множество X будем называть множеством конечной высоты N тогда и только тогда, когда длины всех строго возрастающих последовательностей элементов X ограничены N. Это означает, что для произвольной возрастающей последовательности начиная с некоторого места все элементы становятся одинаковыми.
Рассмотрим теперь функцию перехода F, удовлетворяющую соотношению 
для произвольной разметки 
. Понятно, что при таком условии при итерировании F начиная с некоторого места будет достигнута ее неподвижная точка. Множество 
и функция перехода подбираются таким образом, чтобы эта неподвижная точка являлась решением задачи анализа потоков данных.
На слайде приведена схема итеративного алгоритма анализа потоков данных.
Далее мы более детально рассмотрим возможную природу множества фактов , множества разметок и преобразователей .
Полурешетки
Полурешеткой называется множество, снабженное идемпотентной, коммутативной и ассоциативной операцией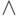 
(определение свойств этой операции приведено на слайде). При наличии такой операции естественным образом индуцируется отношение частичного порядка.
Полурешетка L называется ограниченной тогда и только тогда, когда в ней существуют наибольший TL и наименьший 
элементы.
Функция f называется монотонной, если она сохраняет отношение порядка и дистрибутивной, если она является гомоморфизмом относительно полурешеточной операции. Можно показать, что дистрибутивная функция всегда монотонна.