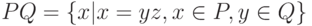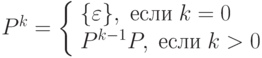Лексический анализ
Использование грамматик для лексического анализа
Нетрудно заметить, что большинство распознаваемых лексем носят четко заданную структуру и потому возникает естественное желание применить к задаче лексического анализа теорию языков, т.е. описать с помощью какого-либо формализма характер цепочек, принимаемых на вход, а затем автоматически сгенерировать по этому описанию лексический анализатор.
Действительно, легко выписать, например, праволинейную грамматику для распознавания идентификаторов:
letter -> 'a'..'z' | 'A'..'Z' | '_' digit -> '0'..'9' ident -> letter | letter tail tail -> letter | digit | letter tail | digit tail
Как мы уже видели, по такой грамматике можно сгенерировать конечный автомат, который распознавал бы правильно сформированные идентификаторы.
Однако исторически сложилось, что для описания лексических свойств чаще используется другой формализм - регулярные выражения, к рассмотрению которых мы сейчас и перейдем.
Регулярные выражения
Определим следующие операции над множествами:
Тогда регулярные выражения над алфавитом T и языки, представляемые ими, могут быть определены следующим образом:
- Символ
 , представляющий пустое множество, является регулярным выражением.
, представляющий пустое множество, является регулярным выражением. -
 является регулярным выражением и представляет множество
является регулярным выражением и представляет множество  .
. - Для каждого символа
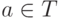 a является регулярным выражением и представляет множество {a}.
a является регулярным выражением и представляет множество {a}. - Если p и q - регулярные выражения, представляющие множества P и Q , то (pq) , (p+q) и (p*) являются регулярными выражениями, представляющими множества PQ,
 и P* соответственно.
и P* соответственно.
Отметим, что в этом определении подразумевается следующая система приоритетов: знак * обладает наивысшим приоритетом, за ним следует символ конкатенации, за которым следует символ |. Приоритеты можно изменять с помощью использования скобок.
Пример. Регулярное выражение 1(0+1)*1+1 представляет множество цепочек, начинающихся и заканчивающихся символом 1.
Упомянем без доказательства, что регулярные выражения эквивалентны праволинейным грамматикам. Таким образом, регулярным выражениям также соответствует естественный класс распознавателей в виде конечных автоматов.
Пример. Рассмотренная выше грамматика для идентификатора может быть записана с помощью следующего регулярного выражения: Letter (Letter | Digit)*.
Построение лексического анализатора по регулярному выражению
По имеющемуся регулярному выражению легко написать лексический анализатор вручную. Ниже приведен пример лексического анализа идентификатора, взятый из демонстрационного компилятора C-бемоль.
if (Char.IsLetter (src [pos]) || src [pos] == '_')
{
int fst = pos;
do
++ pos;
while (pos != src.Length &&
(Char.IsLetterOrDigit (src [pos]) || src [pos]=='_'));
string name = src.Substring (fst, pos - fst);
object tag = keys_table [name];
if (tag != null)
return new Token.Single (new Coor (fname, fst, pos), (Token.Tag) tag);
return new Token.Ident (new Coor (fname, fst, pos), name);
}В этом фрагменте производятся следующие действия:
- анализ первого символа (буква или символ подчеркивания?)
- продвижение вперед по исходной строке, покуда мы встречаем буквы, цифры или символ подчеркивания
- проверка, не является ли разобранный идентификатор ключевым словом?
- если это действительно ключевое слово, то выдается соответствующий лексический класс (ключевое слово, Single ), вместе с привязкой к исходному тексту и точным значением ключевого слова
- если это не ключевое слово, то это идентификатор, который и выдается вместе с привязкой к исходному тексту и его именем.