Селекция признаков
10.3. Селекция на основе проверки статистических гипотез
Этот метод относится к скалярной селекции признаков.
Рассмотрим значение признаков как реализацию случайных величин. Методами математической статистики можно выяснить их распределение. Если распределение совпадает для разных классов, то признак не различает эти классы; если распределения различны, то признак их различает. Такова суть метода селекции на основе проверки статистических гипотез.
Таким образом, задача скалярной селекции на основе проверки статистических гипотез решается путем оценивания дискриминантной способности каждого отдельного признака.
10.3.1. Постановка задачи. Пусть  признак.
Пусть также известны его значения для разных классов
признак.
Пусть также известны его значения для разных классов  и
и 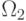 . Тогда
задача состоит в оценке, существенно ли различаются распределения
признака для разных классов.
. Тогда
задача состоит в оценке, существенно ли различаются распределения
признака для разных классов.
Примем следующие соглашения. Обозначим через  и
и  две
гипотезы:
две
гипотезы:
-
 – значения признаков отличаются существенно – нуль-гипотеза.
– значения признаков отличаются существенно – нуль-гипотеза. -
 - значения признаков отличаются несущественно – альтернативная гипотеза.
- значения признаков отличаются несущественно – альтернативная гипотеза.
10.3.2. Общая теория проверки гипотез.
Пусть
-
 – случайная величина с известной плотностью и неизвестным параметром
– случайная величина с известной плотностью и неизвестным параметром  ,
, -
 – экспериментальные значения
– экспериментальные значения  ,
, -
 – статистика, где плотность есть
– статистика, где плотность есть  .
.
Тогда гипотезы примут вид:  и
и  .
Задача состоит в построении интервала
.
Задача состоит в построении интервала  такого, что в
такого, что в  высокая вероятность
выполнения гипотезы
высокая вероятность
выполнения гипотезы  .
.
Пусть  – дополнение к
– дополнение к  .
Тогда, если
.
Тогда, если  попадает в
попадает в  , то принимается
, то принимается  , иначе отвергается.
, иначе отвергается.
Назовем вероятностью ошибки решения следующую величину:

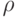 выбирается заранее и называется уровнем значимости:
выбирается заранее и называется уровнем значимости: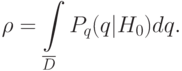
Случай известной дисперсии.
Пусть
-
 – неизвестное среднее,
– неизвестное среднее, -
 – известная дисперсия.
– известная дисперсия.
У нормализованных признаков дисперсия равна единице, следовательно, дисперсия известна.
Оценка  задается следующим образом:
задается следующим образом:

 .
Тогда гипотезы примут вид:
.
Тогда гипотезы примут вид: 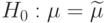 и
и  .
.В данном случае статистика имеет вид:

 – среднеквадратичное отклонение для
– среднеквадратичное отклонение для  .
.По центральной предельной теореме имеем:

Далее,  . Следовательно, находим доверительный интервал
. Следовательно, находим доверительный интервал  по
по 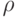 :
т.к.
:
т.к.  , то
, то 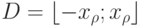 .
Для уровня значимости
.
Для уровня значимости 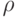 интервал принятия гипотезы
интервал принятия гипотезы 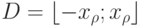 выбирается как интервал, в котором q лежит с вероятностью
выбирается как интервал, в котором q лежит с вероятностью  .
.
Случай неизвестной дисперсии. Если дисперсия неизвестна, то оценка


Если  гауссова величина, то
гауссова величина, то  имеет
имеет  -распределение Стьюдента с
-распределение Стьюдента с  степенями свободы.
Тогда доверительный интервал
степенями свободы.
Тогда доверительный интервал 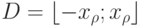 вычисляется по таблицам.
вычисляется по таблицам.
10.3.3. Приложение к селекции признаков
Наша основная забота теперь – проверить отличие 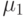 и
и 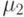 между средними значениями признака в двух
классах.
между средними значениями признака в двух
классах.
Пусть
 – значение признака в первом классе со средним
– значение признака в первом классе со средним 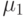 . Соответственно,
. Соответственно,
 - значение признака во втором классе со средним
- значение признака во втором классе со средним 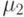 .
.
Предположим, что дисперсии одинаковы в обоих классах. Пусть 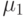 и
и 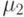 – средние для значений признаков в
первом и втором классе соответственно. Тогда соответствующие гипотезы
имеют вид:
– средние для значений признаков в
первом и втором классе соответственно. Тогда соответствующие гипотезы
имеют вид:
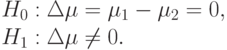
Для решения о близости двух классов мы проверим эти гипотезы.
Пусть  .
.
Гипотеза о равенстве параметров распределения говорит о попадании в
этот интервал величины  , где
, где  и
и  – случайные величины, причем
– случайные величины, причем

Для случая неизвестной дисперсии статистика имеет вид:


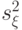 имеет
имеет  распределение с
распределение с 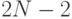 степенями свободы.
степенями свободы.Если  – нормально распределенные с одинаковыми дисперсиями,
тогда случайная величина
– нормально распределенные с одинаковыми дисперсиями,
тогда случайная величина  имеет
имеет  -распределение Стьюдента с
-распределение Стьюдента с 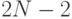 степенями свободы.
степенями свободы.
Если числа прецедентов в обоих классах не совпадают, то формулы модифицируются.
10.3.4. Мера различия плотностей признаков.
Если средние значения различаются, и дисперсии очень большие, то признак может не обладать хорошими разделительными свойствами. Средние значения могут не совпадать и хорошо разделяться, но при больших дисперсиях признак становиться неудовлетворительным. Поэтому нужна информация о перекрытиях между классами. Рассмотрим способ анализа информации о перекрытии плотностей распределения признаков.
Принимать решение, к какому классу отнести объект будем по значению  . Пусть
. Пусть  и
и  –
ошибки при пороге классификации
–
ошибки при пороге классификации  .
.
Идеальным случаем является случай, когда  , т.е. у признака нет
селективных способностей:
, т.е. у признака нет
селективных способностей: 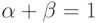 . Рассмотрим параметрическую кривую:
. Рассмотрим параметрическую кривую:  .
Тогда в качестве меры различия распределений можно использовать
площадь разности между кривой реального случая и идеального случая,
которая выражается следующим интегралом
.
Тогда в качестве меры различия распределений можно использовать
площадь разности между кривой реального случая и идеального случая,
которая выражается следующим интегралом



