Нейросетевые информационные модели сложных инженерных систем

Дифференцированная оценка степени корректности обратной задачи на основе кластерного анализа сетью Кохонена

Обратная задача может считаться условно корректной, если в признаковом пространстве выходных переменных имеются области, где обратное отображение однозначно (как в случае системы B с промежуточными значениями скачка h ). Для рассмотренных в предыдущем пункте однопараметрических систем области корректности могут быть выявлены при графическом представлении экспериментальных данных. Отделение областей условной корректности в многомерных пространствах параметров является качественно более сложной задачей. В этом разделе предлагается исследовать возможности нейросетевых алгоритмов адаптивной кластеризации данных для дифференциальных оценок областей условной корректности.

При произвольном распределении точек в многомерном пространстве задача таксономии (т.е. разделения всех точек на несколько компактных групп, называемых кластерами) является достаточно сложной, несмотря на то, что имеется целый ряд методов ее решения. Ситуация дополнительно усложняется в важном практическом случае, когда число кластеров заранее не известно.

На классе нейросетевых алгоритмов также предложено несколько подходов [4.5, 4.6, 4.12, 4.13]. Классическим является предложенный Т.Кохоненом [4.5] алгоритм построения самоорганизующейся карты, которая представляет собой отображение многомерного распределения точек на двумерную решетку с регулярным соседством между узлами. При этом близким узлам на карте отвечают близкие вектора в исходном многомерном пространстве, т.е. сохраняется не только структура разбиения точек на кластеры, но и отношения топологической близости между ними.

Если для приложений достаточно только оценки плотности распределения точек по кластерам с сохранением лишь ближнего порядка в кластеризации, то такое разбиение может быть выполнено более эффективно на основе модели " нейронного газа " [4.12, 4.13], в которой соседство узлов не фиксировано, а динамически меняется по мере улучшения кластеризации. В относительно недавней модификации метода, получившей название " расширяющийся нейронный газ " [4.13], переменными являются не только отношения соседства, но и число нейронов-кластеров.

В данной лекции более подробно рассматриваются приложения более часто используемой карты Кохонена.

Метод дифференциальной оценки степени некорректности задачи

Основная идея предлагаемого метода дифференциальной оценки степени некорректности обратной или комбинированной задачи состоит в реализации следующего плана:

• Построить распределение векторов обучающей выборки по кластерам, содержащим близкие по величине параметров наблюдения. Кластеризация ведется по выходным компонентам Y для чисто обратной задачи, или по совокупности входных и выходных компонент (X,Y) для комбинированного отображения (X,Y)=F(X,Y) ;
• Провести обучение набора (по числу кластеров) малых нейросетей с обратным распространением на данных каждого кластера, оценить ошибку обучения (и, если в распоряжении имеется достаточно данных, ошибку обобщения). Провести набор статистики по результатам обучения нескольких вариантов с различными реализациями случайной инициализации весов. Для получения несмещенных оценок следует учесть, что кластеры могут содержать разное число векторов;
• Поставить в соответствие каждому кластеру данных количественную степень некорректности отображения в области данного кластера. В качестве нее может выступать величина, пропорциональная локальной ошибке обучения для данного кластера;
• Выбрать неприемлемый уровень некорректности (в простейшем случае при помощи порогового правила) для построения гибридной системы, аналогичной малым экспертам [4.4], которая дает регуляризованное решение с локальной оценкой точности в областях с "малой" некорректностью, и предупреждает пользователя о плохой обусловленности задачи, если запрос относится к области "сильной" некорректности.

Важно отметить, что в данном подходе пользователь получает для каждого запроса к нейросетевой модели адекватную локальную точность получаемого результата, и корректный отказ в выдаче результата в области высокой нерегулярности задачи. Поскольку карта Кохонена дает высокую степень наглядности при изучении распределения экспериментальных данных, то распределение степени некорректности по ней представляет богатый материал для понимания особенностей модели и ее параметров. Неоднородности в "раскраске" карты могут отвечать различным режимам поведения инженерной установки или прибора. При моделировании технических систем это часто может служить указанием на нежелательные (или аварийные!) соотношения параметров при эксплуатации.

Пример выявления области некорректности в модельной задаче

Для иллюстрации предлагаемого метода рассмотрим его применение к уже использовавшимся модельным системам A, B и C. Для простоты рассмотрения (и снижения числа необходимых вычислений) можно применить упрощенный алгоритм получения оценки некорректности. Для этого вместо использования набора малых экспертов ограничимся одним персептроном (без скрытых слоев), входы которого замкнуты на выходы нейронов карты Кохонена, а число выходов совпадает с размерностью признакового пространства выходов задачи. Такая гибридная нейроархитектура, называемая сетью встречного распространения , предложена Р.Хехт-Нильсеном [4.7, 4.8].

Каждый кластер соревновательного слоя Кохонена в сети встречного распространения включает в себя несколько векторов обучающего множества. Предъявление на вход нейросети некоторого вектора вызывает соревнование в слое Кохонена, при этом в результате остается активным лишь один нейрон, возбуждение которого затормозило все остальные нейроны. Выход победившего нейрона (нормированный на единицу) воспринимается персептроном, в итоге формируется вектор выходов нейросети в целом. Нужно отметить, что все входные вектора в пределах одного кластера неразличимы (т.к. им всем соответствует один и тот же победитель), поэтому выходы сети встречного распространения не изменятся, если при смене входных векторов не произойдет переход от одного кластера к другому. Таким образом, нейронная сеть встречного распространения дает кусочно-постоянное приближение к моделируемой функции.

Уклонение кусочно-постоянной поверхности от значений выходных векторов обучающей выборки, соответствующих входам в пределах заданного кластера принимается за оценку степени некорректности в области этого кластера^{11Центры кластеров задают разбиение признакового пространства на многогранники Вороного (в двумерном случае - на ячейки Дирихле ). Все точки в пределах одного многогранника ближе к центроиду соответствующего кластера, чем ко всем остальным кластерам.} .

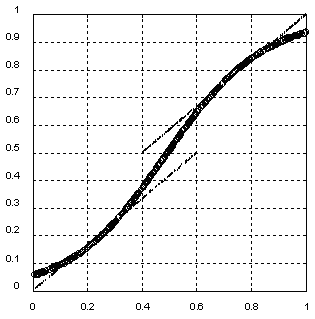
Рис. 4.5. Гладкое регуляризованное решение (кружки) сетью с обратным распространением ошибки для слабо некорректной задачи двузначного отображения, заданного дискретным набором примеров (точки).

На Рис. 4.5 и 4.6 приведено сравнения гладкого регуляризованного решения, определяемого многослойной сетью с обратным распространением, и решения, получаемого при помощи нейросети встречного распространения. Расчеты проведены для системы B для случая относительно слабой некорректности с малым значением величины скачка h.

Легко заметить совершенно различный характер регуляризации, даваемый этими моделями. Уклонение решения от точек обучающего множества в многослойной сети с гладкими переходными функциями охватывает более широкую область, чем собственно область некорректности ( 0.4<Y<0.6 ). Кривая решения и ошибка гладко распространяются в область, где поведение моделируемой системы регулярно.

В случае сети встречного распространения, напротив, регуляризованное решение содержит минимальные ошибки в области регулярности (разбиение на кластеры заметно только вблизи Y=0 и Y=1 ). Решение же в области многозначности функции не является регуляризованным - кластеры со значениями обеих ветвей обратной функции хаотически перепутаны.