НОУ ИНТУИТ | Нейроинформатика. Лекция 2: Решение задач нейронными сетями

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 01.03.2007 | Доступ: свободный | Студентов: 1640 / 246 | Оценка: 4.58 / 4.39 | Длительность: 20:15:00

Тема: Искусственный интеллект и робототехника

Специальности: Программист

|

Вам нравится? Нравится 29 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

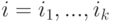Устройство, способное находить точку условного минимума многочлена второго порядка при условиях вида x_i = c_i для i = i_1 ,...,i_k позволяет решать важную задачу - заполнять пробелы в данных (и, в частности, строить линейную регрессию).

Предположим, что получаемые в ходе испытаний векторы данных подчиняются многомерному нормальному распределению:

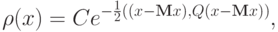
$\rho (x) = Ce^{- \frac{1}{2}((x - {\bf{M}}x),Q(x - {\bf{M}}x))},$

где Mx - вектор математических ожиданий координат, 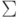$Q = \Sigma^{-1}$ , $\Sigma$ - ковариационная матрица, n - размерность пространства данных,

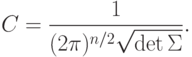
$C = \frac{1}{{(2\pi )^{n/2} \sqrt {\det \Sigma}}} .$

Напомним определение матрицы 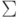$\Sigma$ : $(\Sigma )_{ij} = {\bf{M}}((x_i - {\bf{M}}x_i )(x_j - {\bf{M}}x_j ))$ ,

где M - символ математического ожидания, нижний индекс соответствует номеру координаты.

В частности, простейшая оценка ковариационной матрицы по выборке дает:

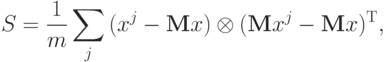
$S = \frac{1}{m}\sum\limits_j {(x^j - {\bf{M}}x)} \otimes ({\bf{M}}x^j - {\bf{M}}x)^{\rm T},$

где m - число элементов в выборке, верхний индекс j - номер вектора данных в выборке, верхний индекс Т означает транспонирование, а $\otimes$ - произведение вектора-столбца на вектор-строку (тензорное произведение).

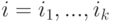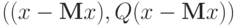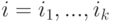Пусть у вектора данных x известно несколько координат: x_i = c_i для i = i_1 ,...,i_k . Наиболее вероятные значения неизвестных координат должны доставлять условный максимум показателю нормального распределения - многочлену второго порядка $((x - {\bf{M}}x),Q(x - {\bf{M}}x))$ (при условии x_i = c_i для i = i_1 ,...,i_k ). Эти же значения будут условными математическими ожиданиями неизвестных координат при заданных условиях.

Таким образом, чтобы построить сеть, заполняющую пробелы в данных, достаточно сконструировать сеть для поиска точек условного минимума многочлена

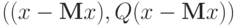
$((x - {\bf{M}}x),Q(x - {\bf{M}}x))$

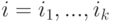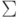при условиях следующего вида: x_i = c_i для i = i_1 ,...,i_k . Матрица связей Q выбирается из условия $Q = \Sigma^{-1}$ , где $\Sigma$ - ковариационная матрица (ее оценка по выборке).

На первый взгляд, пошаговое накопление $Q = \Sigma^{-1}$ по мере поступления данных требует слишком много операций - получив новый вектор данных требуется пересчитать оценку $\Sigma,$ а потом вычислить $Q = \Sigma^{-1}$ . Можно поступать и по-другому, воспользовавшись формулой приближенного обрашения матриц первого порядка точности:

$(\Sigma + \varepsilon \Delta )^{-1} = \Sigma^{-1} - \varepsilon \Sigma^{-1} \Delta \Sigma^{-1} + o(\varepsilon ).$

Если же добавка $\Delta$ имеет вид $\Delta = y \otimes y^{\rm T}$ , то

$(\Sigma + \varepsilon \Delta )^{-1} = \Sigma^{-1} - \varepsilon (\Sigma^{-1} y) \otimes (\Sigma^{-1} y)^{\rm T} + o(\varepsilon ).$

( 10)

Заметим, что решение задачи (точка условного минимума многочлена) не меняется при умножении Q на число. Поэтому полагаем:

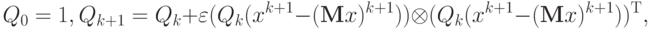
$Q_0 = 1,{\rm{ }}Q_{k + 1} = Q_k + \varepsilon (Q_k (x^{k + 1} - ({\bf{M}}x)^{k + 1} )) \otimes (Q_k (x^{k + 1} - ({\bf{M}}x)^{k + 1} ))^{\rm T} ,$

где 1 - единичная матрица, 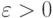$\varepsilon >0$ - достаточно малое число, $x^{k + 1}$ - k +1 -й вектор данных, $({\bf{M}}x)^{k + 1}$ - среднее значение вектора данных, уточненное с учетом $x^{k + 1}$ :

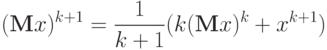
$({\bf{M}}x)^{k + 1} = \frac{1}{{k + 1}}(k({\bf{M}}x)^k + x^{k + 1} )$

В формуле для пошагового накопления матрицы Q ее изменение 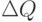$\Delta Q$ при появлении новых данных получается с помощью вектора $y=x^{k + 1} - ({\bf{M}}x)^{k + 1}$ , пропущенного через сеть: $(\Delta Q)_{ij} = \varepsilon z_i z_j$ , где z=Qy. Параметр $\varepsilon$ выбирается достаточно малым для того, чтобы обеспечить положительную определенность получаемых матриц (и, по возможности, их близость к истинным значениям Q ).

Описанный процесс формирования сети можно назвать обучением. Вообще говоря, можно проводить формальное различение между формированием сети по явным формулам и по алгоритмам, не использующим явных формул для весов связей ( неявным ). Тогда термин "обучение" предполагает неявные алгоритмы, а для явных остается название "формирование". Здесь мы такого различия проводить не будем.

Если при обучении сети поступают некомплектные данные $x^{k + 1}$ с отсутствием значений некоторых координат, то сначала эти значения восстанавливаются с помощью имеющейся сети, а потом используются в ее дальнейшем обучении.

Во всех задачах оптимизации существенную роль играет вопрос о правилах остановки: когда следует прекратить циклическое функционирование сети, остановиться и считать полученный результат ответом? Простейший выбор - остановка по малости изменений: если изменения сигналов сети за цикл меньше некоторого фиксированного малого $\sigma$ (при использовании переменного шага $\sigma$ может быть его функцией), то оптимизация заканчивается.

До сих пор речь шла о минимизации положительно определенных квадратичных форм и многочленов второго порядка. Однако самое знаменитое приложение полносвязных сетей связано с увеличением значений положительно определенных квадратичных форм. Речь идет о системах ассоциативной памяти [2.4, 2.5, 2.6, 2.7, 2.9, 2.10, 2.12].

Предположим, что задано несколько эталонных векторов данных x^1 ,...,x^m и при обработке поступившего на вход системы вектора x требуется получить на выходе ближайший к нему эталонный вектор. Мерой сходства в простейшем случае будем считать косинус угла между векторами - для векторов фиксированной длины это просто скалярное произведение. Можно ожидать, что изменение вектора x по закону

$x' = x + h\sum\limits_k {x^k (x^k ,x)} ,$

( 11)

где h - малый шаг, приведет к увеличению проекции x на те эталоны, скалярное произведение на которые (x^k ,x) больше.

Ограничимся рассмотрением эталонов, и ожидаемых результатов обработки с координатами $\pm 1$ . Развивая изложенную идею, приходим к дифференциальному уравнению

$\begin{array}{l} \frac{{dx}}{{dt}} = - {\rm{grad}}H, \\ H = H_0 + \theta H_1 ,{\rm{ }}H_0 (x) = - \frac{1}{2}\sum\limits_k {(x^k ,x)}^2 ,{\rm{ }}H_1 (x) = \frac{1}{2}\sum\limits_i {(x_i^2 - 1)^2 ,} \\ {\rm{grad}}H_0 = - \sum\limits_k {x^k (x^k ,x)} ,{\rm{(grad}}H_1 )_j = (x_j^2 - 1)x_j , \\ \end{array}$

( 12)

где верхними индексами обозначаются номера векторов-эталонов, нижними - координаты векторов.

Функция H называется " энергией " сети, она минимизируется в ходе функционирования. Слагаемое H_0 вводится для того, чтобы со временем возрастала проекция вектора x на те эталоны, которые к нему ближе, слагаемое H_1 обеспечивает стремление координат вектора x к $\pm 1$ . Параметр $\theta$ определяет соотношение между интенсивностями этих двух процессов. Целесообразно постепенно менять $\theta$ со временем, начиная с малых $\theta <1$ , и приходя в конце концов к $\theta >1$ .

Подробнее системы ассоциативной памяти рассмотрены в "Нейронные сети ассоциативной памяти" . Здесь же мы ограничимся обсуждением получающихся весов связей. Матрица связей построенной сети определяется функцией H_0 , так как ${\rm{(grad}}H_1 )_j = (x_j^2 - 1)x_j$ вычисляется непосредственно при j -м нейроне без участия сети. Вес связи между i -м и j -м нейронами не зависит от направления связи и равен

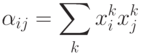$\alpha_{ij} = \sum\limits_k {x_i^k x_j^k}$

( 13)

Эта простая формула имеет чрезвычайно важное значение для развития теории нейронных сетей. Вклад k -го эталона в связь между i -м и j -м нейронами ( x_i^k x_j^k ) равен +1, если i -я и j -я координаты этого эталона имеют одинаковый знак, и равен -1, если они имеют разный знак.

В результате возбуждение i -го нейрона передается j -му (и симметрично, от j -го к i -му), если у большинства эталонов знак i -й и j -й координат совпадают. В противном случае эти нейроны тормозят друг друга: возбуждение i -го ведет к торможению j -го, торможение i -го - к возбуждению j -го (воздействие j -го на i -й симметрично). Это правило образования ассоциативных связей (правило Хебба) сыграло огромную роль в теории нейронных сетей.

Дальше >>

Авторизоваться

Нейроинформатика

Решение задач нейронными сетями

Вопросы и ответы