|
Коллеги, спасибо за очень информативный и полезный курс. Прошёл три лекции. Столкнулся с проблемой, что обе модели не могут закончить расчёт по причине ограничения бесплатной версии "создано максимально допустимое число динамически создаваемых агентов (50000)". По скриншотам Лекции 2 видно, что да, модель создает гораздо больше 50000 агентов. В принципе, мне то и диплом не особо нужен. Но хотелось бы выполнить практические работы. Нет ли возможности откорректировать эту проблему? Или может я чего не так делаю? Еще раз спасибо за прекрасный курс! |
Модель обработки запросов сервером
Добавление параметров и элементов управления
Активный объект может иметь параметры. Параметры обычно используются для задания статических характеристик объекта. Но значения параметров при необходимости можно изменять во время работы модели. Для этого нужно написать код обработчика события, то есть действий, которые должны выполняться при изменении значения параметра.
Создайте параметр time_mean объекта delay.
- В Палитре выделите Основная.
- Перетащите элемент Параметр на диаграмму класса Main и разместите ниже объекта delay, чтобы было видно, к какому объекту относится параметр.
- Перейдите на панель Свойства (Рис. 1.57).
- В поле Имя введите имя параметра time_mean (среднее время). По этому имени параметр будет доступен из кода.
- Задайте тип параметра double.
- В поле Значение по умолчанию установите 180. Если значение не задано явно, по правилам Java оно будет равно нулю.
- Выделите объект delay.
- На панели Свойства в поле Время задержки вместо выражения exponential(1/180.0) введите выражение exponential(1/time_mean).
Пусть вы хотите изменять среднее время обработки запросов time_mean в ходе моделирования. Используйте для этого элемент управления - бегунок.
- Откройте палитру Элементы управления и перетащите элемент Бегунок из палитры на диаграмму класса Main (Рис. 1.58).
- Поместите бегунок под параметром time_mean, чтобы было понятно, что с помощью этого бегунка будет меняться среднее время обработки запросов объектом delay.
- Пусть вы хотите варьировать среднее время от 1 до 300. Поэтому введите 1 в поле Минимальное значение:, а 300 - в поле Максимальное значение: (Рис. 1.59).
- Установите флажок Связать с: и в активизированное поле введите time_mean.
Пусть теперь вы хотите также изменять ёмкость буфера в ходе моделирования. Используйте для этого также бегунок.
- Откройте палитру Элементы управления и перетащите элемент Бегунок из палитры на диаграмму класса Main (Рис. 1.59).
- Поместите бегунок под объектом queue, чтобы было понятно, что с помощью этого бегунка будет меняться вместимость данного объекта, имитирующего входной буфер.
- Пусть вы хотите варьировать ёмкость буфера от 0 до 15 запросов. Поэтому введите 15 в поле Максимальное значение.
- Установите флажок Связать с: и в активизированное поле введите queue.capacity.
- Запустите модель. Теперь вы можете изменять в процессе моделирования ёмкость входного буфера и среднее время обработки запросов с помощью бегунков. Можете также командой Приостановить приостановить работу модели, изменить значения параметров, а затем продолжить моделирование (Рис. 1.60).
- Остановите модель и перейдите на диаграмму класса Main.
Мы научились добавлять элементы Параметр и Бегунок. Но согласитесь, что какие параметры модели нужно будет менять, и в каких интервалах, заранее определить затруднительно. Также при использовании элемента Бегунок существуют трудности точного установления значения характеристики, так как невозможно предусмотреть нужный масштаб или цену деления Бегунка.
увеличить изображение
Рис. 1.60. Фрагмент работы модели с добавленным элементом Параметр и элементами управления
Существует и другой способ изменения свойств объектов во время выполнения модели: нужно щёлкнуть по элементу, войти в режим редактирования и ввести новое значение в одной из закладок всплывающего окна инспекта. Поэтому заранее не нужно продумывать, значения каких параметров планируется изменять, и не добавлять специальные элементы управления (например, бегунки).
Изменение значения в окне инспекта поддерживается для следующих элементов: простая переменная; параметр; накопитель.
И для следующих типов: численные; логический (boolean); текстовый (String).
- Удалите элемент Бегунок для Параметра time_mean.
- Запустите модель и приостановите её.
- Щёлкните по значку Параметра time_mean.
- Перейдите в режим редактирования (Рис. 1.61).
- Введите новое значение: 240.0.
- Закройте инспект. Рядом с элементом Параметр вы увидите введённое вами значение 240.0.
- Запустите модель с новым свойством объекта delay.
Добавление гистограмм
Теперь добавим на диаграмму нашего потока гистограмму, которая будет отображать собранную временную статистику.
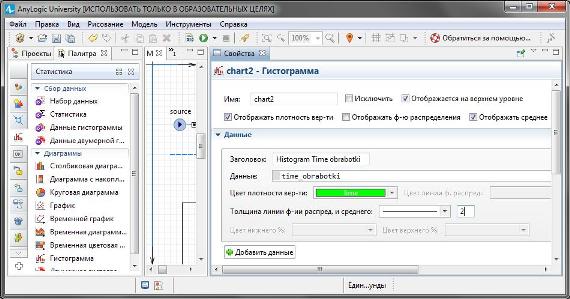
- Перетащите элемент Гистограмма из палитры Статистика в то место графического редактора, куда хотите ее поместить.
- Укажите, какой элемент сбора данных хранит данные, которые вы хотите отображать на гистограмме: щёлкните кнопку Добавить данные и введите в поле Данные имя соответствующего элемента: time_obrabotki (Рис. 1.62). Установите Отображать среднее.
- В поле Заголовок: введите Histogram Time obrabotki.
Добавим на диаграмму нашего потока гистограмму, которая будет отображать собранную вероятностную статистику.
- Перетащите элемент Гистограмма из палитры Статистика.
- Щёлкните кнопку Добавить данные и введите в поле Данные имя элемента: ver_obrabotki. Установите Отображать среднее.
- В поле Заголовок: введите Histogram Ver obrabotki.
- Запустите модель. Фрагмент работы показан на Рис. 1.63.
Изменение времени обработки запросов сервером
Построенная модель соответствует постановке задачи (п. 1.2.1). В ней, с целью упрощения процесса построения первой модели, время обработки запросов сервером было принято распределённым по показательному (экспоненциальному) закону со средним значением T2 = 3 мин.
Однако в модели время обработки поступающих запросов зависит от производительности сервера  оп/с и вычислительной сложности запросов, распределенной по нормальному закону с математическим ожиданием
оп/с и вычислительной сложности запросов, распределенной по нормальному закону с математическим ожиданием  оп и среднеквадратическим отклонением
оп и среднеквадратическим отклонением  оп.
оп.
Кроме того, в модели определяется среднее количество запросов, обработанных за время моделирования 3600 с.
Внесите в модель изменения для аналогичного расчёта времени обработки запросов.
- Удалите элемент Параметр с именем time_mean элемент Бегунок для элемента queue.
- Из палитры Основная перетащите три элемента Параметр на диаграмму класса Main (Рис. 1.64).
- В поле Имя каждого из элементов введите S1_, S2_ и Q_ соответственно. Выберите Тип double.
- В поле Значение по умолчанию каждого из элементов введите 60000000,200000 и 600000 соответственно.
- Перетащите элемент Переменная.
- В поле Имя укажите KolZap.
- Выделите объект delay.
- В поле Время задержки вместо exponential(1/time_mean) введите:(normal(S2_,S1_))/Q_
- Выделите объект sink. В поле Действие при входе к имеющемуся там коду добавьте код:
KolZap=sink.in.count()/9604.0;
Для получения результатов моделирования с доверительной вероятностью
 и точностью
и точностью  нужно выполнить 9604 прогонов модели:
нужно выполнить 9604 прогонов модели:
где
 - табулированный аргумент функции Лапласа, p - ожидаемая вероятность исхода события, в данном случае вероятность обаботки запросов сервером.
- табулированный аргумент функции Лапласа, p - ожидаемая вероятность исхода события, в данном случае вероятность обаботки запросов сервером.
Расчёт проведен для так называемого "худшего" случая, то есть в предположении, что ожидаемая вероятность обработки запросов p = 0,5.
Увеличим время моделирования в AnyLogic-модели в 9604 раз. А так как статистические данные о количестве обработанных запросов собираются за всё время моделирования, увеличенное в 9604 раз, то для получения среднего значения это количество нужно разделить на 9604, что и предусмотрено в коде.
- Показатели моделируемой системы нужно определить в течение 3600 с, поэтому время моделирования в AnyLogic составит 3600*9604 = 34574400 единиц модельного времени.
- В панели Проект выделите Simulation. На странице Модельное время в поле Установить выберите В заданное время.
- В поле Конечное время установите 34574400.
- Запустите модель и дождитесь окончания моделирования.
Результаты моделирования приведены на Рис. 1.65.
Интерпретация результатов моделирования
Для проведения исследований на модели сделайте ещё несколько дополнений и изменений. Можно было бы обойтись и без них, но они улучшат эксплуатацию модели.
- Из палитры Основная перетащите три элемента Параметр на диаграмму агента Main. Разместите их выше параметров S1_, S2_, Q_. Можно перетащить один параметр, скопировать его и вставить остальные два. Если установить свойства первого элемента Параметр, то они будут и в скопированных элементах. Не будем их устанавливать. Установим после копирования и вставки.
- Выделите первый элемент Параметр. В поле Имя: первого параметра введите timeMean - среднее время поступления запросов для обработки на сервере. Оставьте тип double.
- В поле Значение по умолчанию введите 120.
- Выделите объект source. В поле Время между прибытиями вместо 120.0 введите timeMean. Теперь вам при изменении среднего времени поступления запросов не придётся искать нужный код в свойствах объекта модели.
- Выделите второй элемент Параметр. В поле Имя: введите kolProg - количество прогонов модели. Как и в предыдущем случае, при корректировке числа прогонов код в свойствах искать будет не нужно. Оставьте тип double.
- В поле Значение по умолчанию введите 9604.
- Выделите объект sink.
- В поле Действие при входе в имеющемся там коде замените последнюю строку следующей:
KolZap=round(sink.in.count()/kolProg);
На Рис. 1.10. количество обработанных запросов KolZap сервером выдаётся с дробной частью. Теперь, вследствие применения процедуры round, количество запросов будет целым.
Как уже отмечалось, при изменении количества прогонов модели не надо будет искать код для требуемой корректировки. Однако всё-таки потребуется изменить модельное время. Например, если нужно выполнять с моделью 1000 прогонов, то модельное время следует установить равным 3600*1000=3600000.
- Выделите третий элемент Параметр. В поле Имя: введите emkBuf - ёмкость в сообщениях входного буфера сервера. Установите тип int.
- В поле Значение по умолчанию введите 5.
- Выделите объект queue. В поле Вместимость введите emkBuf.
- Запустите модель. Результаты моделирования на Рис. 1.66.
Проведём несколько экспериментов. Будем изменять среднее время поступления запросов timeMean в предположении, что с течением времени количество источников запросов будет расти, то есть timeMean будет уменьшаться. В сторону увеличения будем изменять ёмкость входного буфера emkBuf и производительность Q_ сервера.
Результаты экспериментов приведены в Табл. 1.2.
Из экспериментов 1 и 2 следует, что при увеличении ёмкости входного буфера в два раза вероятность обработки запросов увеличивается незначительно на 0,025, то есть количество обработанных запросов практически одно и тоже. Среднее время обработки одного запроса возрастает в 1,27 раза вследствие увеличения длины очереди в 1,48 раза.
Увеличение интенсивности поступления запросов в три раза при увеличении ёмкости входного буфера в два раза (эксперименты 3 и 4) также не даёт существенного увеличения количества обработанных запросов: 36 вместо 30.
| Показатели | GPSS World | AnyLogic6 | AnyLogic7 |
|---|---|---|---|
| 1) timeMean = 120, emkBuf = 5 | |||
| Количество обработанных запросов | 29 | 29 | 29 |
| Вероятность обработки запросов | 0,97 | 0,971 | 0,97 |
| Среднее время обработки одного запроса | 255,262 | 254,942 | 255,727 |
| Средняя длина очереди запросов к серверу | 1,258 | 1,254 | 1,261 |
| Коэффициент использования сервера | 0,81 | 0,81 | 0,81 |
| 2) timeMean = 120, emkBuf = 10 | |||
| Количество обработанных запросов | 29 | 30 | 30 |
| Вероятность обработки запросов | 0,995 | 0,995 | 0,995 |
| Среднее время обработки одного запроса | 328,328 | 321,54 | 325,017 |
| Средняя длина очереди запросов к серверу | 1,902 | 1,841 | 1,87 |
| Коэффициент использования сервера | 0,833 | 0,831 | 0,831 |
| 3) timeMean = 40, emkBuf = 5 | |||
| Количество обработанных запросов | 36 | 36 | 36 |
| Вероятность обработки запросов | 0,4 | 0,399 | 0,4 |
| Среднее время обработки одного запроса | 1055,335 | 1055,108 | 554,983 |
| Средняя длина очереди запросов к серверу | 4,554 | 4,552 | 4,55 |
| Коэффициент использования сервера | 1 | 1 | 1 |
| 4) timeMean = 40, emkBuf = 10 | |||
| Количество обработанных запросов | 36 | 36 | 36 |
| Вероятность обработки запросов | 0,399 | 0,399 | 0,4 |
| Среднее время обработки одного запроса | 591,86 | 591,304 | 1054,907 |
| Средняя длина очереди запросов к серверу | 9,554 | 9,551 | 9,549 |
| Коэффициент использования сервера | 1 | 1 | 1 |
| 5) timeMean = 40, emkBuf = 10, Q_ = 1000000 | |||
| Количество обработанных запросов | 59 | 60 | 60 |
| Вероятность обработки запросов | 0,666 | 0,665 | 0,667 |
| Среднее время обработки одного запроса | 591,86 | 591,304 | 591,129 |
| Средняя длина очереди запросов к серверу | 8,855 | 8,852 | |
| Коэффициент использования сервера | 1 | 1 | 1 |
| 6) timeMean = 40, emkBuf = 15, Q_ = 2000000 | |||
| Количество обработанных запросов | 90 | 90 | 90 |
| Вероятность обработки запросов | 1 | 1 | 1 |
| Среднее время обработки одного запроса | 74,859 | 75,049 | 75,096 |
| Средняя длина очереди запросов к серверу | 8,864 | 1,096 | 1,128 |
| Коэффициент использования сервера | 0,751 | 0,75 | 0,751 |
При этом уменьшается вероятность обработки запросов в 2,5 раза, а время обработки одного запроса возрастает в 3,25 раза. Возросла и средняя длина очереди запросов к серверу
Коэффициент использования сервера равен 1. Из этого следует, что добиться увеличения вероятности и количества обработанных запросов можно только увеличением производительности сервера.
В экспериментах 5 и 6 увеличена производительность сервера до 1000000 и 2000000 оп/c соответственно.
По сравнению с экспериментом 1 количество обработанных запросов в эксперименте 5 увеличилось в 2 раза, а в эксперименте 6 - в 3 раза (вероятность обработки запросов равна 1). Среднее время обработки одного запроса всё равно примерно в 2 раза больше в эксперименте 5, а в эксперименте 6 - в 3,4 раза меньше. Можно полагать, что такая разница в среднем времени обработки одного запроса вызвана тем, что в эксперименте 5 средняя длина очереди запросов к серверу 8,852, а в эксперименте 6 - 1,128, то есть в 7,85 раза меньше.
Коэффициент использования сервера в эксперименте 6 равен 0,751. Из этого следует, что дальнейщее увеличение производительности сервера приведёт к уменьшению длины очереди и среднего времени обработки одного запроса.
Машинное время выполнения модели в AnyLogic примерно 70…90 с.