|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Необходимые сведения о случайных величинах
5.1 Необходимые сведения о случайных величинах
Случайная величина - одно из основных понятий теории вероятностей. Неформально, случайная величина - это некоторая переменная, принимающая те или иные значения с определенными вероятностями.
Строгое математическое определение случайной величины дается в рамках аксиоматики теории вероятностей.
Определение 5.1 Пусть  - некоторое множество,
- некоторое множество,  - семейство его подмножеств, причем
- семейство его подмножеств, причем
 содержит пустое множество;
содержит пустое множество;- Дополнение любого подмножества из
 снова лежит в
снова лежит в  ;
; - Для любого счетного подсемейства
 объединение
объединение 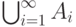 и пересечение
и пересечение  снова лежат в
снова лежат в  .
.
Тогда  называется
называется  -алгеброй.
-алгеброй.
Пример 5.1 Рассмотрим отрезок ![[0;1]](/sites/default/files/tex_cache/b8b4326ebb88870f8cc97ab3f59a0867.png) и множество
и множество  , содержащее все интервалы из отрезка
, содержащее все интервалы из отрезка ![[0;1]](/sites/default/files/tex_cache/b8b4326ebb88870f8cc97ab3f59a0867.png) . Чтобы
. Чтобы  было
было  -алгеброй, необходимо, чтобы
-алгеброй, необходимо, чтобы  содержало также все полуинтервалы, отрезки, их любые счетные объединения и пересечения. Если множество
содержало также все полуинтервалы, отрезки, их любые счетные объединения и пересечения. Если множество  не содержит других подмножеств, кроме перечисленных, то
не содержит других подмножеств, кроме перечисленных, то  называется борелевской
называется борелевской  -алгеброй. Её элементы называются борелевскими множествами.
-алгеброй. Её элементы называются борелевскими множествами.
Определение 5.2 Пусть  -
-  -алгебра на множестве
-алгебра на множестве  . Отображение
. Отображение ![P:A\rightarrow [0;1]](/sites/default/files/tex_cache/5500b691e7287e183cc45770eefbb8f5.png) называется вероятностной мерой на
называется вероятностной мерой на 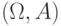 , если
, если
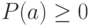 для всех
для всех  ;
; ;
;-
Для любого счетного семейства
 , где
, где 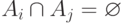 при
при  , выполняется
, выполняется

Величину 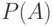 будем называть вероятностью наступления события
будем называть вероятностью наступления события  .
.
Через  обозначим вероятность события
обозначим вероятность события  при условии, что событие
при условии, что событие 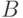 произошло.
произошло.  называется условной вероятностью и при
называется условной вероятностью и при  вычисляется по формуле:
вычисляется по формуле:

Отношения между условными вероятностями устанавливают следующие две важные теоремы.
Теорема 5.1 Пусть  - случайные события, причем
- случайные события, причем  , события
, события  попарно несовместны и
попарно несовместны и  для всех
для всех  . Тогда
. Тогда
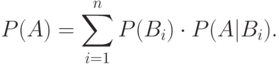
Теорема 5.2 (Теорема Байеса) Пусть  ,
, 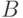 - два случайных события. Тогда
- два случайных события. Тогда

Определение 5.3 Вероятностным пространством называется тройка  , где
, где
 - некоторое множество, элементы которого называются элементарными исходами;
- некоторое множество, элементы которого называются элементарными исходами; - некоторая
- некоторая  -алгебра на множестве
-алгебра на множестве  ; множества из
; множества из  называются событиями; каждое событие
называются событиями; каждое событие  заключается в осуществлении одного из исходов
заключается в осуществлении одного из исходов  .
. - вероятностная мера на
- вероятностная мера на 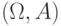 .
.
Определение 5.4 Пусть  - вероятностное пространство. Случайной величиной называется любая функция
- вероятностное пространство. Случайной величиной называется любая функция  такая, что для любого борелевского множества
такая, что для любого борелевского множества 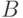 в семействе
в семействе  существует его прообраз
существует его прообраз 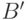 :
:  .
.
Другими словами, случайная величина - это некоторая переменная, принимающая те или иные значения с определенными вероятностями.
Определение 5.5 Случайные величины  , называются независимыми, если для любых борелевских множеств
, называются независимыми, если для любых борелевских множеств 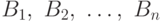 имеем
имеем

Таким образом, наступление одного события  не меняет вероятности наступления другого события
не меняет вероятности наступления другого события  .
.
Важнейшей характеристикой случайной величины  служит ее распределение вероятностей. Закон распределения случайной величин - соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Если различные значения величины образуют конечную или бесконечную последовательность, то распределение вероятностей задается указанием этих значений
служит ее распределение вероятностей. Закон распределения случайной величин - соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Если различные значения величины образуют конечную или бесконечную последовательность, то распределение вероятностей задается указанием этих значений  и соответствующих им вероятностей
и соответствующих им вероятностей 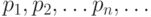 , то есть вероятностей всех событий
, то есть вероятностей всех событий  . Случайные величины указанного типа называются дискретными.
. Случайные величины указанного типа называются дискретными.
Закон распределения дискретной случайной величины может быть задан:
- Аналитически
- Таблично
- Графически
Во всех других случаях распределение вероятностей задается указанием вероятности  для каждого действительного значения
для каждого действительного значения 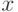 вероятности
вероятности 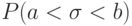 или каждого интервала
или каждого интервала  .
.
Определение 5.6 Пусть  - случайная величина, а функция
- случайная величина, а функция 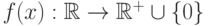 удовлетворяет условиям:
удовлетворяет условиям:

Тогда случайная величина  называется непрерывной, а функция
называется непрерывной, а функция 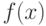 называется её плотностью вероятности.
называется её плотностью вероятности.
Закон распределения неприрывной случайной величины может быть задан в виде:
-
функции распределения
 случайной величины
случайной величины  , определяемой равенством:
, определяемой равенством:  ;
; -
плотности распределения
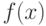 , определяемой как производная от функции распределения:
, определяемой как производная от функции распределения:  .
.
Функция распределения однозначно определяется через плотность распределения:

Свойства фунции распределения:
- плотность распределения принимает только неотрицательные значения:
 ;
; - площадь фигуры, ограниченной графиком плотности распределения и осью абцисс, равна единице:

Числовые характеристики случайных величин
Определение 5.7 Пусть  - вероятностное пространство. Математическим ожиданием случайной величины
- вероятностное пространство. Математическим ожиданием случайной величины  называется величина
называется величина
![M[\xi] = \int\limits_\Omega \xi(\omega)\ P(d\omega).](/sites/default/files/tex_cache/dc88a6e03326103964c64546cb43b9d0.png)
Здесь множество  рассматривается как объединение событий
рассматривается как объединение событий 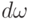 , вероятность которых -
, вероятность которых -  .
.
Рассмотрим два важных частных случая.
Для дискретной случайной величины, принимающей значения  с вероятностями
с вероятностями  , величина
, величина 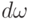 превращается в событие, состоящее из одного исхода. Тогда
превращается в событие, состоящее из одного исхода. Тогда
![M[\xi]=\sum\limits_{i=1}^n x_i p_i.](/sites/default/files/tex_cache/2ba698ff113e3365db9d3a684293f1df.png)
Для непрерывной случайной величины с функцией плотности 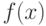 в интеграле можно сделать замену переменной:
в интеграле можно сделать замену переменной: 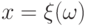 . Тогда будем иметь:
. Тогда будем иметь:
![M[\xi] = \int\limits_{-\infty}^{\infty} x\cdot f(x)\ dx.](/sites/default/files/tex_cache/779a89af7e11a5a8c9370df66a4aae55.png)
Определение 5.8 Дисперсией случайной величины  называется число
называется число ![D[\xi] = M[(\xi - M\xi)^2]](/sites/default/files/tex_cache/70d1c246371e32be8806332cec106ec6.png) .
.
Снова нас интересуют два важных частных случая:
![D[\xi] = \sum_{i=1}^n (x_i-M{\xi})^2\cdot p_i\ \ \text{для дискретной случайной величины}](/sites/default/files/tex_cache/2889459a7a97af23d85a3528c855fa4e.png)
![D[\xi] = \int\limits_{-\infty}^{\infty} (x-M[\xi])^2 f(x) dx\ \ \text{для непрерывной случайной величины.}](/sites/default/files/tex_cache/b95ba35fea0fc53e77d4f92428fa9786.png)
Дисперсия случайной величины показывает разброс значений относительно математического ожидания.
Цепи Маркова
Определение 5.9 Цепью Маркова называют такую последовательность случайных величин 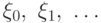 , что для любых значений
, что для любых значений 

Другими словами, цепь Маркова - последовательность случайных величин, каждая из которых зависит только от предыдущей случайной величины.
Цепь Маркова ассоциируется с некоторой величиной, принимающей случайные значения в дискретные моменты времени. Поэтому исход " " можно сформулировать другими словами: "в момент времени
" можно сформулировать другими словами: "в момент времени 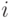 цепь находится в состоянии
цепь находится в состоянии  ".
".
Если множество состояний всех случайных величин 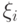 в совокупности конечно, то цепь называется конечной.
в совокупности конечно, то цепь называется конечной.
Если условная вероятность  не зависит от номера
не зависит от номера 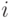 , то цепь называется однородной.
, то цепь называется однородной.
Конечная однородная цепь Маркова задаётся:
- множеством значений
 , которые могут принимать случайные величины;
, которые могут принимать случайные величины; - вектором начальных вероятностей
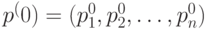 , с которыми случайная величина
, с которыми случайная величина  принимает значения
принимает значения 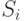 ;
; - матрицей вероятностей переходов
 , в которой
, в которой  (т.е. вероятность того, что из состояния
(т.е. вероятность того, что из состояния 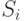 процесс перейдёт в состояние
процесс перейдёт в состояние 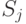 ); отметим, что
); отметим, что
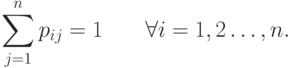
С помощью вектора начальных вероятностей и матрицы переходов можно вычислить стохастический вектор  - вектор, составленный из вероятностей
- вектор, составленный из вероятностей  того, что процесс окажется в состоянии
того, что процесс окажется в состоянии 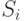 через
через  шагов. Верна формула:
шагов. Верна формула:
 |
( 5.1) |
Векторы  при росте
при росте  в некоторых случаях стабилизируются - сходятся к некоторому вероятностному вектору
в некоторых случаях стабилизируются - сходятся к некоторому вероятностному вектору 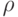 , который можно назвать стационарным распределением цепи. Поскольку оно не меняется от шага к шагу, то формула (5.1) преобразуется в следующее соотношение:
, который можно назвать стационарным распределением цепи. Поскольку оно не меняется от шага к шагу, то формула (5.1) преобразуется в следующее соотношение:
 |
( 5.2) |
Марковская цепь часто изображается в виде орграфа переходов, вершины которого соответствуют состояниям цепи, а дуги - переходам между ними. Вес дуги 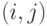 , связывающей вершины
, связывающей вершины 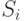 и
и 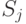 будет равен вероятности перехода из первого состояния во второе.
будет равен вероятности перехода из первого состояния во второе.
Пример 5.2 Пусть дискретная однородная цепь Маркова имеет множество состояний  , распределение вероятности
, распределение вероятности  определяется вектором
определяется вектором  , вероятности переходов заданы матрицей
, вероятности переходов заданы матрицей

Найти:
- матрицу
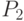 перехода цепи из состояния
перехода цепи из состояния 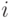 в состояние
в состояние 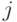 за два шага;
за два шага; - распределение вероятности состояний для
 в момент времени
в момент времени 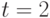 ;
; - вероятность того, что в момент
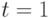 состоянием цепи будет
состоянием цепи будет  ;
; - стационарное распределение.
Решение.
- Матрица перехода однородной цепи Маркова на
 шагов равна
шагов равна  . Для двух шагов имеем:
. Для двух шагов имеем:

- Найдём распределение вероятности в момент времени
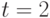 . В формуле (5.1) подставим
. В формуле (5.1) подставим 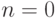 ,
,  и получим:
и получим:

- Найдём распределение вероятности в момент времени
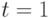 . В формуле (5.1) подставим
. В формуле (5.1) подставим 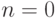 ,
, 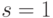 и получим:
и получим:

- Найдём стационарное распределение
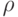 с помощью условия (5.2). Имеем систему уравнений:
с помощью условия (5.2). Имеем систему уравнений:

Последнее условие называется нормировочным. В записанной нами системе всегда одно уравнение является линейной комбинацией других. Следовательно, его можно вычеркнуть. Решим совместно первое уравнение системы и нормировочное. Имеем 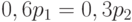 , то есть
, то есть  . Тогда
. Тогда 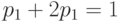 , или
, или  . Следовательно,
. Следовательно,  .
.
Ответ:
- матрица перехода за два шага для данной цепи Маркова имеет вид
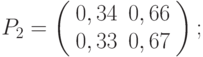
- распределение вероятностей по состояниям в момент
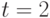 равно
равно 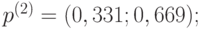
- вероятность того, что в момент
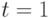 состоянием цепи будет
состоянием цепи будет  , равна
, равна  ;
; - стационарное распределение:

