|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Алгоритмы тестирования на простоту и факторизации
Определение 2.1 Время работы алгоритма 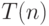 имеет верхнюю оценку
имеет верхнюю оценку 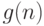 (пишут
(пишут 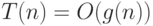 , читают "О большое от
, читают "О большое от 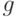 от
от  "), если существует натуральное число
"), если существует натуральное число  и положительная постоянная
и положительная постоянная  такие, что
такие, что  выполняется неравенство:
выполняется неравенство:  .
.
Пример 2.1 Докажем, что функция  имеет верхнюю оценку
имеет верхнюю оценку 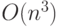 .
.
Действительно, положим  ,
, 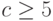 . Тогда
. Тогда 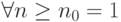 выполняется неравенство
выполняется неравенство  . Следовательно,
. Следовательно,  .
.
Оценка сложности алгоритма - важнейший вопрос для криптографии, поскольку от оценки сложности решающим образом зависит стойкость соответствующей криптосистемы.
Далее мы будем рассматривать алгоритмы (в основном теоретико-числовые) и в большинстве случаев будем приводить оценку сложности представленного алгоритма.
2.1 Тестирование на простоту
Существует два типа критериев простоты: детерминированные и вероятностные. Детерминированные тесты позволяют доказать, что тестируемое число - простое. Практически применимые детерминированные тесты способны дать положительный ответ не для каждого простого числа, поскольку используют лишь достаточные условия простоты.
Детерминированные тесты более полезны, когда необходимо построить большое простое число, а не проверить простоту, скажем, некоторого единственного числа.
В отличие от детерминированных, вероятностные тесты можно эффективно использовать для тестирования отдельных чисел, однако их результаты, с некоторой вероятностью, могут быть неверными. К счастью, ценой количества повторений теста с модифицированными исходными данными вероятность ошибки можно сделать как угодно малой.
На сегодня известно достаточно много алгоритмов проверки чисел на простоту. Несмотря на то, что большинство из таких алгоритмов имеет субэкспоненциальную оценку сложности, на практике они показывают вполне приемлемую скорость работы.
На практике рассмотренные алгоритмы чаще всего по отдельности не применяются. Для проверки числа на простоту используют либо их комбинации, либо детерминированные тесты на простоту.
Детерминированный алгоритм всегда действует по одной и той же схеме и гарантированно решает поставленную задачу. Вероятностный алгоритм использует генератор случайных чисел и дает не гарантированно точный ответ. Вероятностные алгоритмы в общем случае не менее эффективны, чем детерминированные (если используемый генератор случайных чисел всегда дает набор одних и тех же чисел, возможно, зависящих от входных данных, то вероятностный алгоритм становится детерминированным).
2.1.1 Вероятностные тесты простоты
Для того чтобы проверить вероятностным алгоритмом, является ли целое число  простым, выбирают случайное число
простым, выбирают случайное число  ,
, 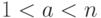 , и проверяют условие алгоритма. Если число
, и проверяют условие алгоритма. Если число  не проходит тест по основанию
не проходит тест по основанию  , то алгоритм выдает результат "Число
, то алгоритм выдает результат "Число  составное", и число
составное", и число  действительно является составным.
действительно является составным.
Если же  проходит тест по основанию
проходит тест по основанию  , нельзя сказать о том, действительно ли число
, нельзя сказать о том, действительно ли число  является простым. Последовательно проведя ряд проверок таким тестом для разных
является простым. Последовательно проведя ряд проверок таким тестом для разных  и получив для каждого из них ответ "Число
и получив для каждого из них ответ "Число  , вероятно, простое", можно утверждать, что число
, вероятно, простое", можно утверждать, что число  является простым с вероятностью, близкой к 1. Если вероятность того, что составное число пройдёт тест, равна
является простым с вероятностью, близкой к 1. Если вероятность того, что составное число пройдёт тест, равна  , то для обеспечения вероятности
, то для обеспечения вероятности  того, что проверенное число является простым, необходимо сделать
того, что проверенное число является простым, необходимо сделать 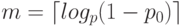 итераций (см.
рис.
1.1}).
итераций (см.
рис.
1.1}).
2.1.2 Тест Ферма
Согласно малой теореме Ферма для простого числа  и произвольного целого числа
и произвольного целого числа  ,
, 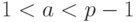 , выполняется сравнение:
, выполняется сравнение:
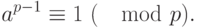
Следовательно, если для нечетного  существует такое целое
существует такое целое  , что
, что 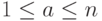 ,
, 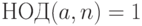 и
и  , то число
, то число  вероятно простое. Таким образом, получаем следующий вероятностный алгоритм проверки числа на простоту:
вероятно простое. Таким образом, получаем следующий вероятностный алгоритм проверки числа на простоту:
Вход: нечетное целое число  .
.
Выход: "Число  , вероятно, простое" или "Число
, вероятно, простое" или "Число  составное".
составное".
- Выбрать случайное целое число
 ,
, 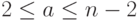 .
. - Вычислить
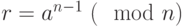 .
. - При
 результат: "Число
результат: "Число  , вероятно, простое". В противном случае результат: "Число
, вероятно, простое". В противном случае результат: "Число  составное".
составное".
На шаге 1 алгоритма мы не рассматриваем числа 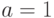 и
и  , поскольку
, поскольку  для любого целого
для любого целого  и
и 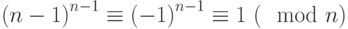 для любого нечетного
для любого нечетного  .
.
Сложность теста Ферма равна:  .
.
Тест имеет существенный недостаток в виде наличия чисел Кармайкла. Это нечетные составные числа, для которых сравнение из формулы выполняется при любом  ,
,  , взаимно простом с
, взаимно простом с  . Для всех
. Для всех  ,
, 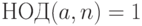 , тест будет выдавать ошибочный результат.
, тест будет выдавать ошибочный результат.
Числа Кармайкла являются достаточно редкими. В пределах до 100000 существует лишь 16 чисел Кармайкла: 561, 1105, 1729, 2465, 2821, 6601, 8911, 10585, 15841, 29341, 41041, 46657, 52633, 62745, 63973, 75361.
2.1.3 Тест Леманна
Если для какого-либо целого числа  , меньшего
, меньшего  , не выполняется условие:
, не выполняется условие:
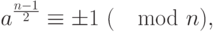
то число  - составное. Если это условие выполняется, то число
- составное. Если это условие выполняется, то число  - возможно простое, причем вероятность ошибки не превышает 50%.
- возможно простое, причем вероятность ошибки не превышает 50%.
Таким образом, получаем следующий вероятностный алгоритм проверки числа на простоту:
Вход: нечетное целое число  .
.
Выход: "Число  , вероятно, простое" или "Число
, вероятно, простое" или "Число  составное".
составное".
- Выбрать случайное целое число
 ,
, 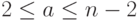 .
. - Вычислить
 .
. - При
 и
и 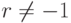 результат: "Число
результат: "Число  составное". В противном случае результат: "Число
составное". В противном случае результат: "Число  , вероятно, простое".
, вероятно, простое".
Сложность теста Леманна равна 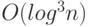 .
.
2.1.4 Тест Соловея-Штрассена
В основе этого теста лежит следующая теорема:
Теорема 1.28 (критерий Эйлера) Нечетное число  является простым тогда и только тогда, когда для любого целого числа
является простым тогда и только тогда, когда для любого целого числа  ,
,  , взаимно простого с
, взаимно простого с  , выполняется сравнение:
, выполняется сравнение:
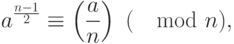 |
( 2.1) |
где  - символ Якоби от параметров
- символ Якоби от параметров  и
и  .
.
Критерий Эйлера лежит в основе следующего вероятностного теста числа на простоту:
Вход: нечетное целое число  .
.
Выход: "Число  , вероятно, простое" или "Число
, вероятно, простое" или "Число  составное".
составное".
- Выбрать случайное целое число
 ,
,  .
. - Вычислить
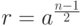 .
. - При
 и
и 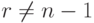 результат: "Число
результат: "Число  составное".
составное". - Вычислить символ Якоби
 .
. - При
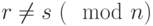 результат: "Число
результат: "Число  составное". В противном случае результат: "Число
составное". В противном случае результат: "Число  , вероятно, простое".
, вероятно, простое".
На шаге 1 мы снова не рассматриваем числа  и
и  , поскольку в силу свойств символа Якоби сравнение в формуле (2.1) для этих чисел выполняется при любом нечетном
, поскольку в силу свойств символа Якоби сравнение в формуле (2.1) для этих чисел выполняется при любом нечетном  . Если
. Если 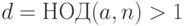 , то
, то 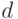 делит и число
делит и число  , вычисляемое на шаге 2. Таким образом, при проверке неравенства
, вычисляемое на шаге 2. Таким образом, при проверке неравенства  на шаге 3 автоматически проверяется условие
на шаге 3 автоматически проверяется условие  .
.
Сложность теста Соловэя-Штрассена определяется сложностью вычисления символа Якоби и равна  .
.
Для теста Соловея-Штрассена не существует чисел, подобных числам Кармайкла, то есть составных чисел, которые были бы эйлеровыми псевдопростыми по всем основаниям  .
.
2.1.5 Тест Миллера-Рабина
На сегодняшний день для проверки чисел на простоту чаще всего используется тест Миллера-Рабина, основанный на следующем наблюдении. Если  - простое, и
- простое, и 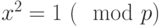 , то
, то  или
или  .
.
Пусть число  нечетное и
нечетное и  , где
, где  - нечетное. По малой теореме Ферма, если
- нечетное. По малой теореме Ферма, если  - простое, то
- простое, то  для любого натурального числа
для любого натурального числа  . Из нашего наблюдения следует, что, в ряду элементов
. Из нашего наблюдения следует, что, в ряду элементов  при каком-либо
при каком-либо  мы будем иметь
мы будем иметь 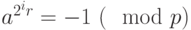 и
и 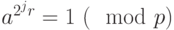 при
при  .
.
Это свойства лежит в основе следующего теста:
Вход: нечетное целое число  .
.
Выход: "Число  , вероятно, простое" или "Число
, вероятно, простое" или "Число  составное".
составное".
- Представить
 в виде
в виде  , где число
, где число  - нечетное.
- нечетное. - Выбрать случайное целое число
 ,
,  , взаимно простое с
, взаимно простое с  .
. - Вычислить
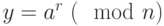 .
. - При
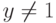 и
и 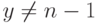 выполнить следующие действия.
выполнить следующие действия.
- Результат: "Число
 , вероятно, простое".
, вероятно, простое".
В результате выполнения теста для простого числа  в последовательности
в последовательности  обязательно перед 1 должна появиться
обязательно перед 1 должна появиться 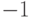 (или, что то же самое,
(или, что то же самое, 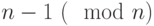 ). Это означает, что для простого числа
). Это означает, что для простого числа  единственными решениями сравнения
единственными решениями сравнения 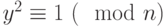 являются
являются 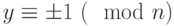 . Если число
. Если число  составное и имеет
составное и имеет  различных простых делителей (то есть не является степенью простого числа), то по китайской теореме об остатках существует
различных простых делителей (то есть не является степенью простого числа), то по китайской теореме об остатках существует 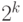 решений сравнения
решений сравнения 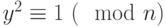 . Действительно, для любого простого делителя
. Действительно, для любого простого делителя 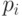 числа
числа  существует два решения указанного сравнения:
существует два решения указанного сравнения: 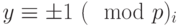 .
Поэтому
.
Поэтому  таких сравнений дают
таких сравнений дают 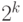 наборов решений по модулям
наборов решений по модулям 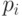 , содержащих элементы
, содержащих элементы  .
.
Сложность теста Миллера-Рабина равна  . Вероятность ошибки, то есть того, что тест объявит составное число простым, не более
. Вероятность ошибки, то есть того, что тест объявит составное число простым, не более  .
.
2.1.6 N - 1-алгоритмы генерации простых чисел
Перечислим некоторые теоремы, которые могут быть использованы для генерации доказуемо простых чисел [1].
Теорема 2.1 (Прот, 1878) Пусть  , где
, где  ,
,  , и
, и  не делит
не делит  . Тогда
. Тогда  - простое тогда и только тогда, когда
- простое тогда и только тогда, когда
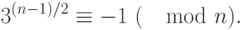 |
( 2.2) |
Для генерации простого числа нужно перебирать числа  и
и  и для каждого варианта проверять условие (2.2). Когда условие будет выполнено, полученное число
и для каждого варианта проверять условие (2.2). Когда условие будет выполнено, полученное число  будет простым.
будет простым.
Недостатком этого подхода является плохое распределение генерируемых простых чисел: все они будут иметь вид 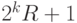 для большого
для большого  и не очень большого
и не очень большого  . В примере 1.42 мы также видели, что чем меньше простые делители числа
. В примере 1.42 мы также видели, что чем меньше простые делители числа  , тем легче осуществить дискретное логарифмирование по модулю
, тем легче осуществить дискретное логарифмирование по модулю  . Это делает генерируемые на основе теоремы Прота простые числа мало пригодными, например, для криптосистемы и электронной подписи Эль-Гамаля.
. Это делает генерируемые на основе теоремы Прота простые числа мало пригодными, например, для криптосистемы и электронной подписи Эль-Гамаля.
Теорема 2.2 (Диемитко, 1988) Пусть 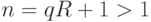 , где
, где  - нечетное простое число,
- нечетное простое число,  - четное, и
- четное, и  . Если существует целое число
. Если существует целое число  такое, что
такое, что
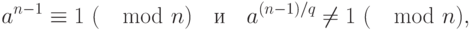
то  простое число.
простое число.
С помощью этой теоремы генерировать простые числа можно итерационно. На вход каждой итерации подаётся какое-либо простое число  . Во время итерации перебираются числа
. Во время итерации перебираются числа  и
и  и проверяются условия теоремы Диемитко. Как только все условия выполнены, мы получили новое простое число
и проверяются условия теоремы Диемитко. Как только все условия выполнены, мы получили новое простое число  , порядок которого примерно вдвое больше, чем у исходного простого числа
, порядок которого примерно вдвое больше, чем у исходного простого числа  . Итерации можно начинать с какого-либо известного простого числа, а заканчивать, когда полученное простое число достигнет требуемого размера.
. Итерации можно начинать с какого-либо известного простого числа, а заканчивать, когда полученное простое число достигнет требуемого размера.
На заключительной итерации желательно выбирать как можно меньшее число  . Тогда у полученного простого числа
. Тогда у полученного простого числа  будет большой простой делитель
будет большой простой делитель  . Если подобрать достаточно малое
. Если подобрать достаточно малое  не получится, может потребоваться выполнить заново предыдущую итерацию для получения нового числа
не получится, может потребоваться выполнить заново предыдущую итерацию для получения нового числа  .
.
Эта теорема лежала в основе алгоритма генерации простых чисел для алгоритма цифровой подписи ГОСТ 34.10-94, пока этот алгоритм не был заменён на новый, основанный на группе точек эллиптической кривой.


 .
.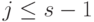 и
и 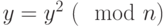 .
.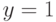 результат: "Число
результат: "Число  .
.