|
Где можно посмотреть информацию о физических ограничениях на значения характеристик компьютеров |
Квантовые процессоры на переходах Джозефсона
Организация сверхпроводящих кубитов в квантовый процессор
Одними из первых вопросов системной организации сверхпроводящих кубитов на ПД в функционально полный квантовый процессор являются вопросы о том, как лучше объединить массив кубитов в единую систему.
Можно сделать так, чтобы каждый из кубитов массива был связан с общим для всех высокодобротным колебательным  контуром, собственная частота которого существенно отличается от резонансных частот отдельных кубитов. Высокая добротность нужна для того, чтобы контур почти не отбирал от кубитов энергию и мало влиял на динамику каждого из них. И в то же время изменение состояния любого из кубитов через общий контур влияет на все другие кубиты.
контуром, собственная частота которого существенно отличается от резонансных частот отдельных кубитов. Высокая добротность нужна для того, чтобы контур почти не отбирал от кубитов энергию и мало влиял на динамику каждого из них. И в то же время изменение состояния любого из кубитов через общий контур влияет на все другие кубиты.
Например, в "линейке" зарядовых кубитов, структура которой изображена на рис. 10.2 справа, такой контур может быть включен последовательно с общим сверхпроводящим "резервуаром" СП.
В случае потоковых кубитов весь их массив может быть размещен в отверстии общей сверхпроводящей "катушки" индуктивности. На рис. 10.9 в качестве примера приведена микрофотография экспериментального 4-кубитного квантового регистра, объединенного такой общей сверхпроводящей "катушкой".
Мы иллюстрируем лишь принцип: внутри контура катушки могут быть не 4, а даже и 1000 кубитов. Из-за того, что суммарный магнитный поток в таком контуре квантуется, уже небольшие изменения собственного магнитного потока сквозь любой из кубитов сразу же влияют на состояние всех других кубитов.
Экспериментальные исследования с пока еще небольшими (4- и 16-кубитными) квантовыми регистрами, расположенными в отверстии общей сверхпроводящей "катушки" индуктивности, показали, что система в целом ведет себя в полном соответствии с ее теоретической квантово-механической моделью. Кубиты легко переводятся в сплетенные состояния и в пределах времени когерентности ведут себя как взаимосогласованный ансамбль.
В большом массиве возможен также вариант, когда каждый кубит взаимодействует через слабую емкостную или индуктивную связь только со своими ближайшими соседями, и только совокупность всех таких связей объединяет кубиты в систему. Такой вариант, его возможности и недостатки сейчас еще всесторонне анализируются теоретически и экспериментально.
Другим системным вопросом является индивидуальная адресация к каждому или хотя бы к некоторым из кубитов в большом их массиве. Перспективной представляется матричная организация с адресацией к заданному потоковому кубиту через две независимые системы ортогональных сверхпроводящих шин. Пропускание электрического тока определенной величины одновременно через две таких шины создает импульсы магнитного потока, требуемые для считывания состояния кубита. При этом с кубитов, на которые подается магнитный поток, созданный током лишь через одну из шин, считывания не происходит. Такая система уже экспериментально испытана, и показано, что она функционирует. Влияние процесса считывания на декогерентизацию не выбранных кубитов было незначительным. Однако нужны еще дополнительные исследования.
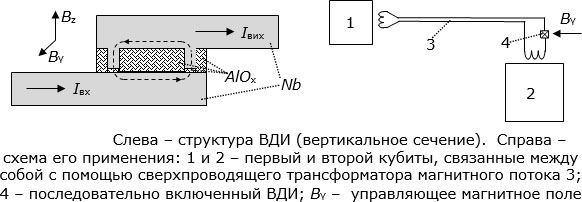
Следующий системный вопрос – это возможность оперативной установки и прерывания связей между некоторыми кубитами массива, связей между ними и внешними схемами, между отдельными подсистемами квантового процессора. Экспериментально показана возможность такого оперативного управления в случае, когда связь осуществляется через сверхпроводящую линию трансформатора магнитного потока. Для этого в линию последовательно включают т.н. "вертикальный джозефсоновский интерферометр" (ВДИ, англ. Vertical Josephson Interferometer – VJI). Его трехслойная структура 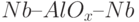 в вертикальном сечении показана на
рис.
10.10 слева.
в вертикальном сечении показана на
рис.
10.10 слева.
При ее изготовлении перед технологической операцией вакуумного напыления верхнего сверхпроводника (напр., из ниобия) в относительно толстом (10–300 нм) слое изолятора вытравливают углубление так, чтобы после напыления 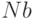 между нижним и верхним сверхпроводниками остались лишь тонкие туннельные барьеры из
между нижним и верхним сверхпроводниками остались лишь тонкие туннельные барьеры из  толщиной
толщиной  нм. Образовавшийся ВДИ с двумя ПД на
рис.
10.10 слева отмечен замкнутой штриховой линией циркулирующего сверхпроводящего тока. Величину этого тока можно регулировать, изменяя горизонтальный магнитный поток
нм. Образовавшийся ВДИ с двумя ПД на
рис.
10.10 слева отмечен замкнутой штриховой линией циркулирующего сверхпроводящего тока. Величину этого тока можно регулировать, изменяя горизонтальный магнитный поток 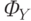 сквозь его вертикальное отверстие. А от этого зависит то, при каком значении "транспортного" тока
сквозь его вертикальное отверстие. А от этого зависит то, при каком значении "транспортного" тока 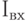 , текущего в сверхпроводящем трансформаторе, суммарный ток через один из ПД превысит критический, и сверхпроводимость разрушится. Т.е. таким образом можно точно регулировать максимальную величину тока через сверхпроводящий трансформатор.
, текущего в сверхпроводящем трансформаторе, суммарный ток через один из ПД превысит критический, и сверхпроводимость разрушится. Т.е. таким образом можно точно регулировать максимальную величину тока через сверхпроводящий трансформатор.
Справа на рис. 10.10 показана схема включения ВДИ в электрическую цепь сверхпроводящего трансформатора 3 между потоковыми кубитами 1 и 2. Экспериментальные измерения показали, что коэффициент передачи магнитного потока можно таким образом контролировано изменять минимум в 40 раз с частотой порядка нескольких мегагерц.
Еще один системный вопрос заключается в возможности временного запоминания квантового состояния кубитов с последующим возвращением их в то же самое состояние. С этой целью предложено использовать высокодобротные пьезоэлектрические резонаторы, изготовленные с помощью технологии НЭМС (наноэлектромеханических систем). Квантовая информация в таких резонаторах может сохраняться в течение десятков-сотен наносекунд. Восстановление квантового состояния происходит с надежностью, лучше 90%. Это важно, так как ряд уже предложенных программ квантовых вычислений предусматривают использование такой памяти.
И, наконец, еще одним системным вопросам является возможность передачи через внутреннюю шину связи произвольной квантовой информации от одной подсистемы процессора к другой. Это можно осуществить через линию из последовательно соединенных сверхпроводниками зарядовых кубитов. Исследована точность такой передачи в зависимости от коэффициента передачи между звеньями, от количества звеньев, продолжительности передачи и от величины динамического шума.