Язык программирования Си
Язык Си подобен обоюдоострому лезвию, при помощи которого легко создать как изысканное блюдо, так и кровавое месиво.
Язык Си был создан в 1972 г. Деннисом Ритчи в ходе разработки операционной системы (ОС) Unix. Практически вся ОС была написана на Си. Большие выразительные возможности и легкость расширения способствовали быстрому распространению этого языка. Компиляторы для языка Си доступны практически для всех существующих на данный момент ОС и платформ.
В отличие от большинства языков высокого уровня (Ада, Алгол и др.), которые начинали применять только после принятия соответствующих стандартов на них, язык Си был создан как рабочий инструмент эффективного кодирования и не претендовал на общественное использование. Спецификация языка была определена в книге Кернигана Б. и Ритчи Д. (перевод на русский язык [8]). Эта книга оставалась неформальным стандартом на язык Си вплоть до 1989 г., когда был принят стандарт ANSI. На данный момент существует еще ISO-стандарт на этот язык.
В качестве отличительных особенностей языка Си можно выделить:
- препроцессорные директивы;
- необходимость определять переменные, но возможность это делать в любом месте (до первого использования переменной);
- использование фигурных скобок {} для структуризации текста программы;
- обязательное наличие функции main()
3.1. Типы в языке Си
Как и в любом языке программирования, в Си определены базовые типы и набор механизмов для задания произвольных пользовательских типов на основе базовых.
Базовые типы
В качестве базовых в языке Си определены следующие типы.
Целочисленные:
- char - целый длиной не менее 8 бит (интерпретируется обычно как литера);
- short /short int/ - короткий целый;
- int - целый;
- long - длинный целый.
Для всех целочисленных типов можно определить, будут они знаковые или нет. Это делается прибавлением слова unsigned или signed перед названием типа (по умолчанию - signed).
В ранних компьютерах целые числа представлялись своим модулем и отдельным знаковым битом. В первых машинах размещали знак в младшем разряде, а когда стала возможной параллельная обработка, знак переместили в старший разряд, аналогично общепринятой бумажной нотации. Однако использование представления "знак и модуль" приводило к усложнению структуры вычислителя, поскольку для положительных и отрицательных чисел требовались разные схемы обработки.
Более удачным оказалось представление отрицательных чисел в виде дополнения, поскольку одна и та же схема могла выполнять и сложение, и вычитание. Некоторые разработчики выбирали дополнение до единицы, когда  получалось из
получалось из  путем простого инвертирования всех бит (так называемый обратный код). Другие выбирали дополнение до двойки, когда
путем простого инвертирования всех бит (так называемый обратный код). Другие выбирали дополнение до двойки, когда  получалось путем инвертирования всех бит и прибавлением единицы. Недостатком первого способа было наличие двух форм представления нуля (0...0 и 1...1). Это неприятно, особенно если доступные инструкции сравнения являются неадекватными. Различия этих форм показаны в табл. 3.1.
получалось путем инвертирования всех бит и прибавлением единицы. Недостатком первого способа было наличие двух форм представления нуля (0...0 и 1...1). Это неприятно, особенно если доступные инструкции сравнения являются неадекватными. Различия этих форм показаны в табл. 3.1.
| Десятичное представление | Прямой код | Дополнительный код | Обратный код | |
|---|---|---|---|---|
| Знак | Модуль | |||
| 2 | 0 | 010 | 010 | 010 |
| 1 | 0 | 001 | 001 | 001 |
| 0 | 0 | 000 | 000 | 000 или 111 |
| -1 | 1 | 001 | 111 | 110 |
| -2 | 1 | 010 | 110 | 101 |
Сегодня во всех компьютерах используется арифметика с дополнением до двойки, обычно называемая просто дополнительным кодом. Как мы видим, у отрицательных чисел старший разряд равен 1. Добавление спецификации unsigned означает, что весь код следует воспринимать как модуль числа. При этом нижняя строчка таблицы, соответствующая -2 в десятичной системе и представляющая в дополнительном коде 110, будет обрабатываться как десятичное число шесть. Естественно, при signed-спецификации этот же код будет обрабатываться как - 2.
Числа с дробной частью можно представлять в формах с фиксированной и плавающей точкой. В современной аппаратуре для вещественных чисел обычно поддерживается арифметика с плавающей точкой, т.е. число  представляется двумя целыми числами - порядком
представляется двумя целыми числами - порядком  и мантиссой
и мантиссой  , так что
, так что 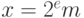 . Это позволяет значительно расширить диапазон представляемых в машине чисел.
. Это позволяет значительно расширить диапазон представляемых в машине чисел.
Вещественные:
- float - вещественный одинарной точности;
- double - вещественный двойной точности;
- long double - вещественный максимальной точности.
Недостатком такого представления является то, что та же память теперь делится между двумя целыми числами: мантиссой числа и его порядком. Это приводит к сокращению числа разрядов мантиссы, а следовательно, к меньшей ее точности. Более того, практически одно и то же число может теперь быть представлено разной комбинацией разрядов: чуть большим или чуть меньшим значением. Т.е. сравнение чисел надо производить с учетом некоторого диапазона чувствительности. Стоит при этом помнить еще и о том, что складывая очень большие и очень маленькие вещественные числа из различных диапазонов, каждое из которых помещается в машинное представление, мы рискуем потерять младшие разряды мантиссы, а значит, и значение малой добавки.
Разработчики аппаратуры шли на различные ухищрения для смягчения этого свойства: отказывались от хранения старшего разряда мантиссы для увеличения ее точности, переходили к удвоенной разрядной сетке, увеличивали основание порядка до 8 и даже до 16. Однако проблемы округления оставались. Известны случаи, когда в подобных машинах можно было найти такие значения x и у, что для некоторого малого положительного ? выполнялось соотношение  , т.е. умножение утрачивало свойство монотонности.
, т.е. умножение утрачивало свойство монотонности.
