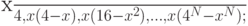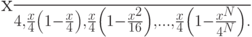Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1275 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы
Лекция 7:

Понятие о методах конечных элементов
A
|
версия для печати
< Лекция 6 || Лекция 7: 12345678 || Лекция 8 >

7.7. Решение нелинейных уравнений с помощью МКЭ

Рассмотрим в качестве простейшего примера уравнение Хопфа

{\frac{{\partial}u}{{\partial}t} + 6u \frac{{{\partial}\mboxit{u}}}{{{\partial}\mboxit{x}}} = 0.} ( 7.18)

Его решение, как и ранее, ищем в виде (7.14), при этом по - прежнему используем базис из "крышечек". После вычислений получаем

{\frac{1}{6} \frac{{dC_{j - 1}}}{dt} + \frac{2}{3} \frac{{dC_j }}{dt} + \frac{1}{6} \frac{{dC_{j + 1}}}{dt} - C_{j - 1}^2 - C_j C_{j - 1} + C_j C_{j + 1} + C_{j + 1}^2 = 0.} ( 7.19)

Если написать дискретизацию (7.19) неявным образом (по величинам на n + 1 - м слое по времени или по аналогии со схемой Кранка - Николсон), то получается нелинейная относительно C_j^{n + 1} система. Ее необходимо решать с помощью метода Ньютона. Можно линеаризовать (7.19) в окрестности C_j^{n} , считая, что

C_j^{n + 1} \approx C_j^{n} + {\tau} \frac{dC_j }{dt}.

Тогда (7.19) преобразуется в следующую линейную относительно величин на n + 1 - м слое по времени запись:

\begin{gather*} \frac{1}{6} \frac{{C_{j - 1}^{n + 1} - C_{j - 1}^{n}}}{\tau} + \frac{2}{3} \frac{{C_j^{n + 1} - C_j^{n}}}{\tau} + \frac{1}{6} \frac{{C_{j + 1}^{n + 1} - C_{j + 1}^{n}}}{\tau} - (C_{j - 1}^{n})^2 - \\ - 2C_{j - 1}^{n}C_{j - 1}^{n + 1} - C_j^{n}C_{j - 1}^{n} - C_j^{n} C_{j - 1}^{n + 1} - C_j^{n + 1} C_{j - 1}^{n} + \\ + C_j^{n} C_{j + 1}^{n} + C_j^{n} C_j^{n + 1} + C_j^{n} C_{j + 1}^{n + 1} + (C_{j + 1}^{n})^2 + 2C_{j + 1}^{n}C_{j + 1}^{n + 1} = 0. \end{gather*}

Эту систему можно решать, используя метод немонотонной прогонки — гибрид метода прогонки и алгоритма Гаусса с выбором ведущего элемента.

Возможен и другой подход — линеаризация исходного уравнения (7.18) и решение получившейся последовательности линейных уравнений для определения приближенного решения задачи.

За рамками этой лекции, кроме технических подробностей, остались численные методы, основанные на применении минимизации функционала квадрата невязки — методы наименьших квадратов, а также методы граничных элементов для решения эллиптических задач.

7.8. Задачи для самостоятельного решения

  1. При решении задачи с использованием метода Ритца на отрезке [0, 4] используются глобальные базисы
    1. \frac{x}{4}, x(4 - x), x(16 - x^2), \ldots , x(4^{N} - x^{N});
    2. \frac{x}{4}, x(4 - x), x^2 (4 - x), \ldots , x^{N} (4 - x);
    3. \frac{x}{4}, \frac{x}{4} \left({1 - \frac{x}{4}}\right), \frac{x}{4} \left({1 - \frac{{x^2}}{{16}}}\right), \ldots , \frac{x}{4} \left({1 - \frac{{x^{N}}}{{4^{N}}}}\right).

    Описать достоинства и недостатки каждого из этих базисов.

Дальше >>
< Лекция 6 || Лекция 7: 12345678 || Лекция 8 >

Вопросы и ответы

вопросов: 0