Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы
Лекция 3:

Численные методы решения уравнений в частных производных гиперболического типа (на примере уравнения переноса)
A
|
версия для печати
< Лекция 2 || Лекция 3: 1234567891011 || Лекция 4 >

3.10. Задачи для самостоятельного решения

  1. Для линейного однородного уравнения переноса
    $ \frac{{\partial}u}{{\partial}t} + a \frac{{\partial}u}{{\partial}x} = 0, a = {const} > 0 $
    построить разностные схемы первого, второго и третьего порядков аппроксимации, используя шаблоны, приведенные на рисунках.

  2. Для линейного однородного уравнения переноса
    $ \frac{{\partial u}}{{\partial}t} + \frac{{\partial}u}{{\partial}x} = 0, $
    построить разностную схему, имеющую второй порядок по времени и четвертый по координате, используя шаблон с точками (t^{n}, x_{m}) (t^{n + 1}, x_{m})(t^{n}, x_{m \pm 1}) (t^{n + 1}, x_{m \pm 1})(t^{n}, x_{m \pm 2}) (t^{n + 1}, x_{m \pm 2}).
  3. Исследовать устойчивость параметрической схемы

    $ \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + \frac{1}{2} \left[{\alpha \frac{{u_{m + 1}^{n + 1} - u_{m - 1}^{n + 1}}}{2h} + (1 -{\alpha}) \frac{{u_{m + 1}^{n} - u_{m - 1}^{n}}}{2h}}\right] = 0, {\alpha} \in \left[{0, 1}\right] = 0 $

    для численного решения линейного уравнения переноса.

  4. Определить, при каких значениях {\alpha} схема

    $ \frac{u_m^{n + 1} - u_m^{n}}{\tau} +{\alpha} \frac{u_{m + 1}^{n} - u_m^{n}}{h} + (1 -{\alpha}) \frac{u_m^{n} - u_{m - 1}^{n}}{h} $

    аппроксимирующая линейное однородное уравнение переноса, является устойчивой.

  5. Для численного решения линейного уравнения переноса

    $ \frac{{\partial}u}{{\partial}t} = \frac{{\partial}u}{{\partial}x} + \frac{{\partial}u}{{\partial}y} $

    предложить разностные схемы первого и второго порядков точности; исследовать их на сходимость.

  6. Исследовать на сходимость схему предиктор - корректор:

    предиктор

    \begin{gather*} \frac{{u_{{m} + 1/2}^{{n} + 1/2} - u_{{m} + 1/2}^{n}}}{{{\tau}/2}} + \frac{{u_{{m} + 1}^{n} - u_m^{n}}}{h} = 0, \\ \frac{{u_{{m} - 1/2}^{{n} + 1/2} - u_{{m} - 1/2}^{n}}}{{{\tau}/2}} + \frac{{u_m^{n} - u_{m - 1}^{n}}}{h} = 0, \end{gather*}

    корректор

    $ \frac{{u_m^{n + 1} - u_m^{n}}}{{{\tau}/2}} + \frac{{u_{{m} + 1/2}^{{n} + 1/2} - u_{{m} - 1/2}^{{n} + 1/2}}}{h} = 0, $

    аппроксимирующую уравнение переноса

    $ \frac{{\partial}u}{{\partial}t} + \frac{{\partial}u}{{\partial x}} = 0. $
  7. Исследовать на сходимость схемы, имеющие шаблоны

    для численного решения уравнения переноса

    $ \frac{{\partial}u}{{\partial}t} + a \frac{{\partial}u}{{\partial}x} = 0, \quad a = {const} > 0. $
  8. Предложить устойчивые схемы первого и второго порядка аппроксимации для численного решения акустической системы

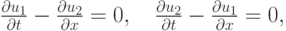
    $ \frac{{{\partial}u_1}}{{\partial}t} - \frac{{{\partial}u_2}}{{\partial}x} = 0, \quad \frac{{{\partial}u_2}}{{\partial}t} - \frac{{{\partial}u_1}}{{\partial}x} = 0, $

    которую можно представить в матричной форме:

    $ \frac{{{\partial}\mathbf{u}}}{{\partial}t} + \mathbf{A} \frac{{{\partial}\mathbf{u}}}{{\partial}x} = 0, u = (u_1 , u_2 )^{T}, \mathbf{A} = \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \\ \end{array} \right) . $
  9. Используя характеристические свойства уравнения переноса

    $ \frac{{\partial}u}{{\partial}t} + a \frac{{\partial}u}{{\partial x}} = 0, \quad a = {const} > 0 $

    построить аппроксимирующую разностную схему на шаблонах, приведенных на рисунках


  10. Предложить гибридную разностную схему для численного решения линейного однородного уравнения переноса, использующую два опорных шаблона, изображенных ниже:

  11. Исследовать на сходимость схему с шаблоном

    для численного решения линейного однородного уравнения переноса.

  12. Исследовать на устойчивость схему с искусственной вязкостью

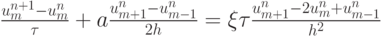
    $ \frac{u_m^{n + 1} - u_m^{n}}{\tau} + a \frac{u_{m + 1}^{n} - u_{m - 1}^{n}}{2h} = \xi{\tau}\frac{u_{m + 1}^{n} - 2u_m^{n} + u_{m - 1}^{n}}{h^2} $

    для решения уравнения переноса

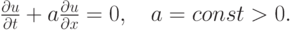
    $ \frac{{\partial}u}{{\partial}t} + a \frac{{\partial}u}{{\partial}x} = 0, \quad a = {const} > 0. $
  13. При каких значениях \xi эта схема совпадает со схемами Лакса, Куранта - Изаксона - Риса, Лакса - Вендроффа?
  14. Показать, что разностные схемы Лакса и Куранта - Изаксона - Риса удовлетворяют условию TVD.
  15. Акустика

    Рассмотрим нестационарное течение жидкости, охватывающее ограниченную область. Требуется предсказать звуковое поле, излучаемое на большом расстоянии от области течения. Акустическая аналогия этой задачи состоит в решении неоднородного волнового уравнения:

    $ \left({\frac{1}{{a_0^2}} \frac{{{\partial}^{2}}}{{\partial t^2}} - {\Delta}}\right) {\varphi} = q , $

    здесь a0 — скорость распространения звука в покоящейся жидкости, \varphi — искомый потенциал скорости, q — интенсивность источника.

    Если жидкость несжимаемая, то a_0 \to \infty и волновое уравнение переходит в уравнение Лапласа.

    Все волны обладают некоторыми общими свойствами. Одним из важных свойств большинства волн является сохранение энергии. Другое свойство состоит в том, что полное смещение среды в волне обычно весьма мало. Поскольку волновое уравнение имеет второй порядок как по пространственным переменным, так и по времени, оно обратимо, если только в уравнении не присутствуют члены, описывающие диссипативные процессы. Следовательно, в алгоритмах для волнового уравнения нежелательны диссипативные ошибки, приводящие к уменьшению амплитуды решения. Выполнение условия обратимости решения в алгоритме гарантирует, что моды не затухают, когда алгоритм устойчив. Поскольку волны часто распространяются на весьма большие расстояния, алгоритм, применяемый для расчета их поведения, должен давать минимальное численное затухание. Наилучшие из подобных алгоритмов являются почти неустойчивыми или могут быть легко переведены в неустойчивое состояние за счет малых ошибок аппроксимации, дополнительных нецентрированных слагаемых в разностном уравнении или нелинейных эффектов, которые не появляются при линейном анализе устойчивости.

    • a) Реализовать разностный алгоритм для численного решения и рассмотреть поведение решений волнового уравнения, представленных в виде суммы двух волн 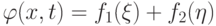\varphi ({x, t}) = f_1 (\xi ) + f_2 ({\eta}), где \xi = x - a_{0}t, \eta = x + a_{0}t. Для этого задать в начальный момент времени ( t = 0 ) потенциал возмущенного движения \varphi(x) в виде функции, например, f_{1}(\xi ), отличной от нуля только на участке 0 \le x_0 \le \xi_0.
    • b) Исследовать распространение волн, если область их распространения с одной стороны ограничена. Как учесть взаимодействие волны со стенкой в численном расчете?
    • c) Рассмотрим систему дифференциальных уравнений:

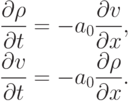
      \begin{gather*} \frac{{{\partial}{\rho}}}{{\partial}t} = - a_0 \frac{{\partial}v}{{{\partial} x}}, \\ \frac{{\partial}v}{{\partial}t} = - a_0 \frac{{{\partial}{\rho}}}{{{\partial} x}} . \end{gather*}

      Уравнения имеют периодические решения вида

      \rho (x, t) = \rho (k)e^{ikx} e^{ - i\omega t}, \\ v(x, t) = v(k)e^{ikx} e^{ - i\omega t},

      где \rho (k) и v(k) — комплексные величины, k — волновое число, отвечающее направлению x. Это действительная величина, которая с длиной волны моды связана соотношением {\lambda} = 2 \pi/k.

      Реализовать следующую конечно - разностную аппроксимацию системы:

      \begin{gather*} \frac{{\rho_{j}^{n} - \rho_{j}^{n - 1}}}{{{\Delta}t}} = - a_0 \frac{{v_{{j} + {1/2}}^{{n} - {1/2}} - v_{{j} - {1/2}}^{{n} - {1/2}}}}{{\Delta}x}, \\ \frac{{v_{{j} - {1/2}}^{{n} + {1/2}} - v_{{j} - {1/2}}^{{n} - {1/2}}}}{{{\Delta}t}} = - a_0 \frac{{{\rho}_{j}^{n} - \rho_{{j} - {1}}^{n}}}{{\Delta}x} . \end{gather*}

      Здесь переменная 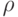\rho определена в центрах ячеек в старый и новый момент времени. Скорость v определена на границах ячеек и в моменты, промежуточные по отношению к тем, в которые определена плотность. Подобные сетки называются разнесенными. Разностная схема называется явным алгоритмом "чехарда" на разнесенной сетке. Вывести условие устойчивости для этой схемы.

    • d) Для акустической системы реализовать неявный конечно - разностный алгоритм:

      \begin{gather*} \rho_{j}^{n} - \rho_{j}^{{n} - {1}} = - \frac{{\Delta {ta}_0 }}{2} \left[{\frac{{(v_{{j} + {1/2}}^{n} - v_{{j} - {1/2}}^{n})}}{{\Delta}x} + \frac{{(v_{{j} + {1/2}}^{{n} - {1}} - v_{{j} - {1/2}}^{{n} - {1}})}}{{\Delta}x}}\right] , \\ v_{{j} + {1/2}}^{n} - v_{{j} + {1/2}}^{{n} - {1}} = - \frac{{{\Delta}{ta}_0 }}{2} \left[{\frac{{(\rho_{{j} + {1}}^{n} - \rho_{j}^{n})}}{{\Delta}x} + \frac{{(\rho_{{j} + {1}}^{{n} - {1}} - \rho_{j}^{{n} - {1}})}}{{\Delta}x}}\right] . \end{gather*}

      Расчетная сетка здесь разнесена по пространству, но не по времени. Новые значения 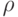\rho и v теперь определяются одновременно на одном и том же шаге по времени. Исследовать устойчивость этой схемы.

      Одной из хороших проверок алгоритма является следующая процедура. Провести расчет на большое число шагов по времени, затем остановить его, изменить знак \delta t и затем выполнить обратный расчет задачи до начального времени t = 0.

    Более подробно качественные свойства рассмотренных здесь алгоритмов обсуждаются в [13.18, С. 145 - 154].

Дальше >>
< Лекция 2 || Лекция 3: 1234567891011 || Лекция 4 >

Вопросы и ответы

вопросов: 0