Лекция 2: Численное решение дифференциальных уравнений в частных производных параболического типа на примере уравнения теплопроводности
2.5. Задачи
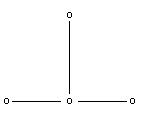
- Исследовать на аппроксимацию и устойчивость схему Ричардсонас шаблоном

аппроксимирующую уравнение теплопроводности
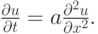
Решение. В силу симметрии шаблона схемы несложно заметить, что ее порядок аппроксимации
 .
.Подстановка решения в виде
 дает квадратное уравнение для определения спектра оператора послойного переходаодин из корней которого при любом значении параметра
дает квадратное уравнение для определения спектра оператора послойного переходаодин из корней которого при любом значении параметра
 по модулю больше единицы, т. е. рассматриваемая схема безусловно неустойчива.
по модулю больше единицы, т. е. рассматриваемая схема безусловно неустойчива.
Выходом из данной ситуации оказывается замена в выражении
величины
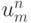 на (схема Франкела - Дюффорта):
на (схема Франкела - Дюффорта):
![$ \frac{{u_m^{n + 1} - u_m^{n - 1}}}{{2{\tau}}} = \frac{a}{h^2} \left[{u_{m - 1}^{n} - \left({u_m^{n + 1} + u_m^{n - 1}}\right) + u_{m + 1}^{n}}\right]
$](/sites/default/files/tex_cache/31e849270ea10b3c6d849f10767f3e23.png)
со следующим шаблоном:
которая разрешается явно относительно
 и безусловно устойчива.
и безусловно устойчива.Однако она обладает лишь условной аппроксимацией:
 , и таким образом, сходимость возможна лишь при
, и таким образом, сходимость возможна лишь при  .
. - Исследовать на аппроксимацию и устойчивость схему Саульева бегущего счета
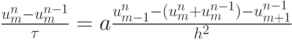
(четные слои, счет справа налево)

(нечетные слои, счет слева направо) со следующим шаблоном:
Решение. Путем подстановки решения в виде
 , несложно проверить, что схема безусловно
устойчива.
, несложно проверить, что схема безусловно
устойчива.Невязка каждого из двух уравнений, вычисленная относительно точек, отмеченных крестиками, имеет порядок
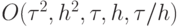 .
.Сложение же невязок из двух рассматриваемых уравнений дает погрешность
 , аналогичную схеме Франкела - Дюфорта.
, аналогичную схеме Франкела - Дюфорта.Схема Саульева допускает значительное улучшение. Достаточно только вычислить значения функции в рамках перехода с данного слоя на следующий два раза — бегущим счетом слева направо и бегущим счетом справа налево — и усреднить результаты. Свойства такого метода расчета предлагается исследовать самостоятельно.
- Исследовать на аппроксимацию и устойчивость схему Алена - Чена

с шаблоном
Ответ. Во - первых, несмотря на то, что в правую часть входит значение функции
 , вычисляемое на верхнем слое, разностное уравнение разрешается относительно
, вычисляемое на верхнем слое, разностное уравнение разрешается относительно  . Схема безусловно устойчива, что является ее достоинством при реализации, однако она имеет порядок аппроксимации
. Схема безусловно устойчива, что является ее достоинством при реализации, однако она имеет порядок аппроксимации  , т.е. схема является условно аппроксимирующей.
, т.е. схема является условно аппроксимирующей. - Выяснить, является ли явная четырехточечная схема с шаблоном

монотонной. Монотонные разностные схемы (по Фридрихсу) — это схемы, которые при записи в виде, разрешенном относительно
 при значениях сеточной функции во всех остальных точках шаблона, имеют неотрицательные коэффициенты. Монотонные разностные схемы не дают паразитные осцилляции в решении. Придумать доказательство утверждения, что из монотонности разностной схемы следует ее устойчивость, предлагается самостоятельно.
при значениях сеточной функции во всех остальных точках шаблона, имеют неотрицательные коэффициенты. Монотонные разностные схемы не дают паразитные осцилляции в решении. Придумать доказательство утверждения, что из монотонности разностной схемы следует ее устойчивость, предлагается самостоятельно.Решение. Представим рассматриваемую схему в виде

где
откуда видно, что схема является монотонной при выполнении условия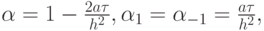
 то есть при . Эта схема условно монотонная.
то есть при . Эта схема условно монотонная.
Заметим, что неявная четырехточечная схема является монотонной, а схема Кранка - Никольсон — условно монотонная.
Исследование монотонности параметрической двуслойной схемы в виде
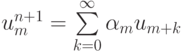 , дает (выкладки опускаем ввиду их громоздкости):
, дает (выкладки опускаем ввиду их громоздкости):
Коэффициенты
 при
при 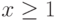 неотрицательны, коэффициент
неотрицательны, коэффициент 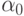 неотрицателен при выполнении условия:
неотрицателен при выполнении условия:
Отсюда видно, что, за исключением неявной четырехточечной схемы с
 , все неявные схемы являются монотонными лишь при условии
, все неявные схемы являются монотонными лишь при условии  .
. - Исследовать на устойчивость и аппроксимацию трехслойную схему

с шаблоном
Ответ. Простое исследование на аппроксимацию данной схемы путем разложения функций в ряд Тейлора дает
 . Схема безусловно устойчива. Кроме того, схема монотонна.
. Схема безусловно устойчива. Кроме того, схема монотонна. - Показать, что решение задачи

( 2.5) представляет собой бегущую волну, распространяющуюся с конечной скоростью, причем при
 на фронте волны решение терпит разрыв первой
производной (т.е. является обобщенным решением).
на фронте волны решение терпит разрыв первой
производной (т.е. является обобщенным решением).Предложить какие - нибудь разностные схемы для численного решения данной задачи, например, применив интегро - интерполяционный метод [12.3]. Почему в этом случае нельзя переписать уравнение в виде

продифференцировав правую часть по x, а затем заменить производные их разностными аппроксимациями?
Решение. Построим решение задачи в переменных бегущей волны:
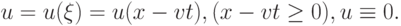
( 2.6) Подставив (2.6) в исходное уравнение, получим следующее обыкновенное дифференциальное уравнение:

( 2.7) Это уравнение интегрируется по


( 2.8) где k — константа интегрирования.
Выражение, стоящее в правой части (2.8), есть поток величины u, а уравнение (2.8) является некоторым законом сохранения. В точке фронта u = 0, в силу непрерывности потока справа и слева от фронта (2.8) должно выполняться, отсюда следует k = 0.
Так как интересуют только нетривиальные решения (2.5), то
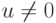 , и можно разделить правую и левую части на u. Тогда получим
, и можно разделить правую и левую части на u. Тогда получим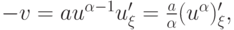
( 2.9) откуда
.![$ u = \left[{\frac{{\alpha v}}{a}(x - vt)}\right]^{1/{\alpha}} $](/sites/default/files/tex_cache/bbf915e2c6dab8328913d20a46f449f3.png)
Из краевых условий при x = 0 имеем
 . Наличие разрывов производной легко проверяется. Уравнение (2.5) записано в дивергентном виде, которому будет соответствовать консервативная схема.
. Наличие разрывов производной легко проверяется. Уравнение (2.5) записано в дивергентном виде, которому будет соответствовать консервативная схема.В [12.9] использован несколько отличный подход к решению задачи.
В [12.4] рассмотрен общий случай, когда коэффициент теплопроводности есть функция K(u):

Подробнее про разностные схемы для аппроксимации уравнения (5.3.1) в [12.4, c. 441 - 463].