Синтаксический анализ
LR(1)-грамматики
Если для КС-грамматики G функция Action, полученная в результате работы алгоритма 4.11., не содержит неоднозначно определенных входов, то грамматика называется LR(1)- грамматикой.
Язык L называется LR(1)-языком, если он может быть порожден некоторой LR(1)-грамматикой.
Иногда используется другое определение LR(1)-грамматики. Грамматика называется LR(1), если из условий
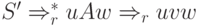

- FIRST(w)=FIRST(y)
следует, что uAy = zBx (то есть u = z, A = B и x = y).
Согласно этому определению, если uvw и uvy -
правовыводимые цепочки пополненной грамматики, у
которых FIRST(w) = FIRST(y) и  - последнее
правило, использованное в правом выводе цепочки uvw, то
правило
- последнее
правило, использованное в правом выводе цепочки uvw, то
правило  должно применяться и в правом разборе
при свертке uvy к uAy. Так как A дает
должно применяться и в правом разборе
при свертке uvy к uAy. Так как A дает 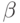 независимо от w, то LR(1)-условие означает, что в FIRST(w) содержится
информация, достаточная для определения того, что uv за один шаг выводится из uA. Поэтому никогда
не может возникнуть сомнений относительно того, как
свернуть очередную правовыводимую цепочку пополненной
грамматики.
независимо от w, то LR(1)-условие означает, что в FIRST(w) содержится
информация, достаточная для определения того, что uv за один шаг выводится из uA. Поэтому никогда
не может возникнуть сомнений относительно того, как
свернуть очередную правовыводимую цепочку пополненной
грамматики.
Можно доказать, что эти два определения эквивалентны. Дадим теперь определение LR(k)-грамматики.
Определение. Пусть  - КС-грамматика
и
- КС-грамматика
и  - полученная из нее пополненная
грамматика. Будем называть G LR(k)-грамматикой для k >= 0, если из условий
- полученная из нее пополненная
грамматика. Будем называть G LR(k)-грамматикой для k >= 0, если из условий
(1) 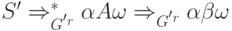
(2) 
(3) FIRSTk(w) = FIRSTk(y)
следует, что  :
:
Грамматика G называется LR-грамматикой, если она LR(k)-грамматика для некоторого k >= 0:
Интуитивно это определение говорит о том, что если 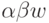 и
и  - правовыводимые цепочки пополненной грамматики,
у которых FIRSTk(w) = FIRSTk(y), и
- правовыводимые цепочки пополненной грамматики,
у которых FIRSTk(w) = FIRSTk(y), и  - последнее правило, использованное в правом выводе цепочки
- последнее правило, использованное в правом выводе цепочки 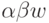 , то
правило
, то
правило  должно использоваться также в правом
разборе при свертке
должно использоваться также в правом
разборе при свертке  к
к  . Так как A даeт
. Так как A даeт 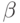 независимо
от w, то LR(k)-условие говорит о том, что в FIRSTk(w)
содержится информация, достаточная для определения того,
что
независимо
от w, то LR(k)-условие говорит о том, что в FIRSTk(w)
содержится информация, достаточная для определения того,
что  за один шаг выводится из
за один шаг выводится из 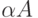 . Поэтому никогда
не может возникнуть сомнений относительно того, как
свернуть очередную правовыводимую цепочку пополненной
грамматики. Кроме того, работая с LR(k)-грамматикой, мы
всегда знаем, допустить ли данную входную цепочку или
продолжать разбор.
. Поэтому никогда
не может возникнуть сомнений относительно того, как
свернуть очередную правовыводимую цепочку пополненной
грамматики. Кроме того, работая с LR(k)-грамматикой, мы
всегда знаем, допустить ли данную входную цепочку или
продолжать разбор.
Пример 4.13. Рассмотрим грамматику G с правилами
S -> Sa|a
Согласно определению, G не LR(0)-грамматика, так как из трeх условий
(1) 
(2) 
(3) FIRST0(e) = FIRST0(a) = e
не следует, что S'a = S: Применяя определение к этой ситуации,
имеем 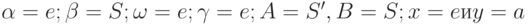 . Проблема здесь заключается в том, что нельзя
установить, является ли S основой правовыводимой цепочки Sa,
не видя символа, стоящего после S (т.е. наблюдая "нулевое"
количество символов). В соответствии с интуицией G не должна
быть LR(0)- грамматикой и она не будет ею, если пользоваться
первым определением. Это определение мы и будем использовать
далее.
. Проблема здесь заключается в том, что нельзя
установить, является ли S основой правовыводимой цепочки Sa,
не видя символа, стоящего после S (т.е. наблюдая "нулевое"
количество символов). В соответствии с интуицией G не должна
быть LR(0)- грамматикой и она не будет ею, если пользоваться
первым определением. Это определение мы и будем использовать
далее.
Пример 4.14. Пусть G - леволинейная грамматика с правилами
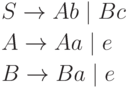
Заметим, что G не является LR(k)-грамматикой ни для какого k.
Допустим, что G - LR(k)-грамматика. Рассмотрим два правых вывода в пополненной грамматике G':
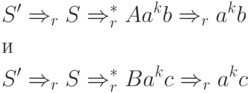
Эти два вывода удовлетворяют условию из определения LR(k)-
грамматики при  : Но так
как заключение неверно, т.е.
: Но так
как заключение неверно, т.е.  , то G - не LR(k)-грамматика.
Более того, так как LR(k)-условие нарушается для всех k, то G -
не LR-грамматика.
, то G - не LR(k)-грамматика.
Более того, так как LR(k)-условие нарушается для всех k, то G -
не LR-грамматика.
Если грамматика не является LR(1), то анализатор типа сдвиг-свертка при анализе некоторой цепочки может достигнуть конфигурации, в которой он, зная содержимое магазина и следующий входной символ, не может решить, делать ли сдвиг или свертку (конфликт сдвиг/свертка), или не может решить, какую из нескольких сверток применить (конфликт свертка/свертка).
В частности, неоднозначная грамматика не может быть LR(1). Для доказательства рассмотрим два различных правых вывода
(1) 
(2) 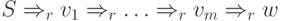 ,
,
Нетрудно заметить, что LR(1) - условие (согласно
второму определению LR(1)-грамматики) нарушается
для наименьшего из чисел i, для которых  .
.
Пример 4.15. Рассмотрим ещe раз грамматику условных операторов:
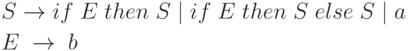
Если анализатор типа сдвиг-свертка находится в конфигурации, такой, что необработанная часть входной цепочки имеет вид else ... $, а в магазине находится ... if E then S, то нельзя определить, является ли if E then S основой, вне зависимости от того, что лежит в магазине ниже. Это конфликт сдвиг/свертка. В зависимости от того, что следует на входе за else, правильной может быть свертка по S -> if E then S или сдвиг else, а затем разбор другого S и завершение основы if E then S else S. Таким образом нельзя сказать, нужно ли в этом случае делать сдвиг или свертку, так что грамматика не является LR(1).
Эта грамматика может быть преобразована к LR(1)-виду следующим образом:
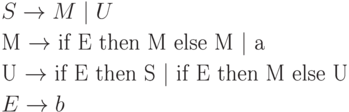
Основная разница между LL(1)- и LR(1)- грамматиками заключается в следующем. Чтобы грамматика была LR(1)- грамматикой, необходимо распознавать вхождение правой части правила вывода, просмотрев все, что выведено из этой правой части и текущий символ входной цепочки. Это требование существенно менее строгое, чем требование для LL(1)-грамматики, когда необходимо определить применимое правило, видя только первый символ, выводимый из его правой части. Таким образом, класс LL(1)-грамматик есть собственный подкласс класса LR(1)-грамматик.
Справедливы также следующие утверждения [2].
Теорема 4.7. Каждый LR(1)-язык является детерминированным КС-языком.
Теорема 4.8. Если L - детерминированный КС-язык, то существует LR(1)-грамматика, порождающая L.
Теорема 4.9. Для любой LR(k)-грамматики для k > 1 существует эквивалентная ей LR(k \Gamma 1)-грамматика.
Доказано, что проблема определения, порождает ли грамматика LR-язык, является алгоритмически неразрешимой.
Восстановление процесса анализа после синтаксических ошибок
Одним из простейших методов восстановления после ошибки при LR(1)-анализе является следующий. При синтаксической ошибке просматриваем магазин от верхушки, пока не найдем состояние s с переходом на выделенный нетерминал A. Затем сканируются входные символы, пока не будет найден такой, который допустим после A. В этом случае на верхушку магазина помещается состояние Goto[s, A] и разбор продолжается. Для нетерминала A может иметься несколько таких вариантов. Обычно A - это нетерминал, представляющий одну из основных конструкций языка, например оператор.
При более детальной проработке реакции на ошибки можно в каждой пустой клетке анализатора поставить обращение к своей подпрограмме. Такая подпрограмма может вставлять или удалять входные символы или символы магазина, менять порядок входных символов.
Варианты LR-анализаторов
Часто построенные таблицы для LR(1)-анализатора оказываются довольно большими. Поэтому при практической реализации используются различные методы их сжатия. С другой стороны, часто оказывается, что при построении для языка синтаксического анализатора типа "сдвиг-свертка" достаточно более простых методов. Некоторые из этих методов базируются на основе LR(1)-анализаторов.
Одним из способов такого упрощения является LR(0)- анализ - частный случая LR-анализа, когда ни при построении таблиц, ни при анализе не учитывается аванцепочка.
Еще одним вариантом LR-анализа являются так называемые SLR(1)-анализаторы (Simple LR(1)). Они строятся следующим образом. Пусть C = {I0, I1, ... , In} - набор множеств допустимых LR(0)-ситуаций. Состояния анализатора соответствуют Ii. Функции действий и переходов анализатора определяются следующим образом.
- Если
![[A \rightarrow u.av] \in I_i \text{ и } goto(I_i, a) = I_j,](/sites/default/files/tex_cache/5e0ffeb04ef83b1d2038ffb8bbaef82f.png) то определим Action[i, a] = shift j.
то определим Action[i, a] = shift j. - Если
![[A \rightarrow u.] \in I_i](/sites/default/files/tex_cache/5228d0ace6f46898e88a648a181e8fbb.png) , то, для всех
, то, для всех  ,
,  , определим Action[i, a] = reduce A -> u
, определим Action[i, a] = reduce A -> u
- Если
![[S' \rightarrow S.] \in I_i](/sites/default/files/tex_cache/f82e462bddf77b658f7b3a70bc978c73.png) , то определим Action[i, $] = accept.
, то определим Action[i, $] = accept. - Если goto (Ii, A) = Ij, где
 , то определим Goto[i, A] = j.
, то определим Goto[i, A] = j. - Остальные входы для функций Action и Goto определим как error.
- Начальное состояние соответствует множеству ситуаций, содержащему ситуацию [S' -> .S]
Распространенным вариантом LR(1)-анализа является
также LALR(1)-анализ. Он основан на объединении (слиянии)
некоторых таблиц. Назовем ядром множества LR(1)-ситуаций
множество их первых компонент (то есть во множестве
ситуаций не учитываются аванцепочки). Объединим все
множества ситуаций с одинаковыми ядрами, а в качестве
аванцепочек возьмем объединение аванцепочек. Функции Action и Goto строятся очевидным образом. Если функция Action таким образом построенного анализатора не имеет
конфликтов, то он называется LALR(1)-анализатором
( LookAhead LR(1)).Если грамматика является LR(1), то в
таблицах LALR(1) анализатора могут появиться конфликты
типы свертка-свертка (если одно из объединяемых состояний
имело ситуации ![[A \to \alpha , a]](/sites/default/files/tex_cache/9772b40ecba4ed9087af8739b423a3da.png) и
и ![[B \to \beta , b]](/sites/default/files/tex_cache/3c01ff31c0fa5b2d7a80b63a74559093.png) , а другое
, а другое ![[A \to \alpha , b]](/sites/default/files/tex_cache/59b3a9d8501ea8d314ef19ea5b8e8152.png) и
и ![[B \to \beta a]](/sites/default/files/tex_cache/fd115f7ef7e41d08126d1212edaf40f1.png) , то в LALR(1) появятся ситуации
, то в LALR(1) появятся ситуации ![[A \to \alpha , \{ a, b\} ]](/sites/default/files/tex_cache/e07ebe44e81669262b2bf1b4cd990271.png) и
и ![[B \to \beta , \{ b, a\} ])](/sites/default/files/tex_cache/f13d0c04d759de3465ebcf7007c6459a.png) . Конфликты типа сдвиг-свертка появиться
не могут, поскольку аванцепочка для сдвига во внимание не
принимается.
. Конфликты типа сдвиг-свертка появиться
не могут, поскольку аванцепочка для сдвига во внимание не
принимается.
