Синтаксический анализ

Контекстно-свободные грамматики и автоматы с магазинной памятью

Пусть G = (N, T, P, S) - КС-грамматика. Введем несколько важных понятий и определений.

Вывод, в котором в любой сентенциальной форме на каждом шаге делается подстановка самого левого нетерминала, называется левосторонним. Если S=>^* u в процессе левостороннего вывода, то u - левая сентенциальная форма. Аналогично определим правосторонний вывод. Обозначим шаги левого (правого) вывода =>_l (=>_r).

Упорядоченным графом называется пара (V,E), где V есть множество вершин, а E - множество линейно упорядоченных списков дуг, каждый элемент которого имеет вид ((v, v₁), (v, v₂), ... , (v, v_n)). Этот элемент указывает, что из вершины v выходят n дуг, причем первой из них считается дуга, входящая в вершину v₁, второй - дуга, входящая в вершину v₂, и т.д.

Упорядоченным помеченным деревом называется упорядоченный граф (V,E), основой которого является дерево и для которого определена функция f : V -> F (функция разметки) для некоторого множества F.

Упорядоченное помеченное дерево D называется деревом вывода (или деревом разбора ) цепочки w в КС-грамматике G = (N, T, P, S), если выполнены следующие условия:

(1) корень дерева D помечен S ;

(2) каждый лист помечен либо , либо e ;

(3) каждая внутренняя вершина помечена нетерминалом ;

(4) если X - нетерминал, которым помечена внутренняя вершина и X₁, ... , X_n - метки ее прямых потомков в указанном порядке, то X -> X₁ ... X_k - правило из множества P ;

(5) Цепочка, составленная из выписанных слева направо меток листьев, равна w.

Процесс определения принадлежности данной строки языку, порождаемому данной грамматикой, и, в случае указанной принадлежности, построение дерева разбора для этой строки, называется синтаксическим анализом. Можно говорить о восстановлении дерева вывода (в частности, правостороннего или левостороннего) для строки, принадлежащей языку. По восстановленному выводу можно строить дерево разбора.

Грамматика G называется неоднозначной, если существует цепочка w, для которой имеется два или более различных деревьев вывода в G.

Грамматика G называется леворекурсивной, если в ней имеется нетерминал A такой, что для некоторой цепочки R существует вывод .

Автомат с магазинной памятью (МП-автомат) - это семерка 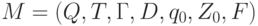, где

(1) Q - конечное множество состояний, представляющих всевозможные состояния управляющего устройства;

(2) T - конечный входной алфавит;

(3) 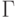- конечный алфавит магазинных символов ;

(4) D - отображение множества в множество конечных подмножеств , называемое функцией переходов ;

(5) - начальное состояние управляющего устройства;

(6) - символ, находящийся в магазине в начальный момент ( начальный символ магазина );

(7) - множество заключительных состояний.

Конфигурация МП-автомата - это тройка (q, w, u), где

(1) - текущее состояние управляющего устройства;

(2) - непрочитанная часть входной цепочки; первый символ цепочки w находится под входной головкой; если w = e, то считается, что вся входная лента прочитана;

(3) - содержимое магазина; самый левый символ цепочки u считается верхним символом магазина; если u = e, то магазин считается пустым.

Такт работы МП-автомата M будем представлять в виде бинарного отношения , определенного на конфигурациях.

Будем писать

если множество D(q, a, Z) содержит (p, v), где и (верхушка магазина слева).

Начальной конфигурацией МП-автомата M называется конфигурация вида (q₀, w, Z₀), где , то есть управляющее устройство находится в начальном состоянии, входная лента содержит цепочку, которую нужно проанализировать, а в магазине имеется только начальный символ Z₀.

>Заключительной конфигурацией называется конфигурация вида (q, e, u), где , то есть управляющее устройство находится в одном из заключительных состояний, а входная цепочка целиком прочитана.

Введем транзитивное и рефлексивно-транзитивное замыкание отношения , а также его степень k > 0 (обозначаемые 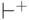, и соответственно).

Говорят, что цепочка w допускается МП-автоматом M, если для некоторых и .

Множество всех цепочек, допускаемых автоматом M называется языком, допускаемым (распознаваемым, определяемым) автоматом M (обозначается L(M) ).

Пример 4.1. Рассмотрим МП-автомат

M = ({q₀, q₁, q₂}, {a, b}, {Z, a, b}, D, q₀, Z, {q₂}),

у которого функция переходов D содержит элементы:

D(q0, a, Z) = {(q0, aZ)},
D(q0, b, Z) = {(q0, bZ)},
D(q0, a, a) = {(q0, aa), {q1, e)},
D(q0, a, b) = {(q0, ab)},
D(q0, b, a) = {(q0, ba)},
D(q0, b, b) = {(q0, bb), (q1, e)},
D(q1, a, a) = {(q1, e)},
D(q1, b, b) = {(q1, e)},
D(q1, e, Z) = {(q2, e)}.

Нетрудно показать, что , где w^R обозначает обращение ("переворачивание") цепочки w.

Иногда допустимость определяют несколько иначе: цепочка w допускается МП-автоматом M, если для некоторого . В таком случае говорят, что автомат допускает цепочку опустошением магазина. Эти определения эквивалентны, ибо справедлива