Языки и их представление
Итак, если сокращать нельзя, достраиваем слово до
ближайшего подходящего квадрата. В данном случае удобнее
достроить слово до 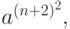 т.к. для достройки до
т.к. для достройки до  нам бы потребовалось перевести
нам бы потребовалось перевести  , т.е. опять что-то сократить.
Напомним, что в КЗ-грамматиках допускается переход аксиомы
в пустую цепочку (
, т.е. опять что-то сократить.
Напомним, что в КЗ-грамматиках допускается переход аксиомы
в пустую цепочку (  ), если аксиома нигде более не встречается в
правых частях правил (т.е. когда из начального ничего получают
другое ничего).
), если аксиома нигде более не встречается в
правых частях правил (т.е. когда из начального ничего получают
другое ничего).
Мы получили несокращающую грамматику. Но широко
используемые при ее построении правила вида  (
(  и т.п.), очевидно, не подходят под определение
НС-грамматики (убедитесь!). Такие "рокировки" , однако, легко
раскрыть через цепочку правил вида
и т.п.), очевидно, не подходят под определение
НС-грамматики (убедитесь!). Такие "рокировки" , однако, легко
раскрыть через цепочку правил вида
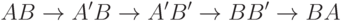
где  и
и 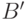 - нигде более в грамматике не используемые
вспомогательные знаки. Отметим, что замену на промежуточные
знаки и обратно на исходные нужно осуществлять в одном и том
же порядке (слева-направо или, наоборот, только справа-налево),
иначе в общем случае (когда назначение A и B в грамматике
различно) возникают лишние цепочки.
- нигде более в грамматике не используемые
вспомогательные знаки. Отметим, что замену на промежуточные
знаки и обратно на исходные нужно осуществлять в одном и том
же порядке (слева-направо или, наоборот, только справа-налево),
иначе в общем случае (когда назначение A и B в грамматике
различно) возникают лишние цепочки.
Так, применение замены

(нарушен порядок замен) при наличии соответствующего прово- кационного окружения допускает подмену B на A:
![x=A\underline{AB}B \xrightarrow[]{*} AA'\underline{AB} \xrightarrow[]{*} A\underline{A'B}A \xrightarrow[]{*} ABAA=y](/sites/default/files/tex_cache/874675281f06ba2a36a1c2c1d8045fbc.png)
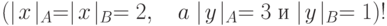
Замена AB на BA в рамках НС-грамматики коротко
обозначается, как и обычный вывод: ![AB \xrightarrow[]{*} BA](/sites/default/files/tex_cache/7df43511c87e6419b1b806b07e23e077.png) .
.
Таким образом, один из возможных наборов правил искомой НС-грамматики имеет следующий вид:
| Правила | Вид получаемой цепочки |
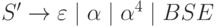 |
BSE |
 |
BCnDn E |
![CD \xrightarrow[]{*} DCA](/sites/default/files/tex_cache/911cef9942fe5b6fa6159501eeaeed11.png) |
BCn-1DCADn-1E |
![CA \xrightarrow[]{*} AC](/sites/default/files/tex_cache/24d3e65e710afce05d1c43e4e0f022d8.png) |
BCn-1(DA)nCE |
| B(DAn)nCnE | |
![BD \xrightarrow[]{*} aaB](/sites/default/files/tex_cache/25bf06e05a9354d5267d9d25d4b570a7.png) |
a2BAn(DAn)n-1CnE |
![BA \xrightarrow[]{*} AB](/sites/default/files/tex_cache/4d04aae848a79972da8e9ab33126af12.png) |
(a2An)nBCnE |
![CE \xrightarrow[]{*} Eaa](/sites/default/files/tex_cache/fae0207204321eb91eb461f07cd9805d.png) |
(a2An)nBEa2n |
![A \xrightarrow[]{*} a](/sites/default/files/tex_cache/4f497238ddcf3f4af4f63007688caed6.png) |
an*n+2nBEa2n |
![BE \xrightarrow[]{*} a^4](/sites/default/files/tex_cache/2e476ece433216ad5076d7b39436ab42.png) |
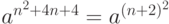 |
Машины Тьюринга
Формально машина Тьюринга ( Tm ) - это 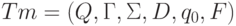 , где
, где
Q - конечное множество состояний;
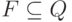 - множество заключительных состояний;
- множество заключительных состояний;
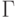 - множество допустимых ленточных символов; один из них, обычно обозначаемый B, - пустой символ
- множество допустимых ленточных символов; один из них, обычно обозначаемый B, - пустой символ
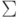 - множество входных символов, подмножество \Gamma, не
включающее B,
- множество входных символов, подмножество \Gamma, не
включающее B,
D функция переходов, отображение из 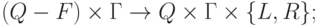 для некоторых аргументов функция D может быть не определена.
для некоторых аргументов функция D может быть не определена.
 - начальное состояние.
- начальное состояние.
Так определенная машина Тьюринга называется детерминированной. Недетерминированная машина
Тьюринга для каждой пары 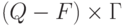 может иметь
несколько возможных переходов. В начале n ячеек ленты
содержат вход
может иметь
несколько возможных переходов. В начале n ячеек ленты
содержат вход 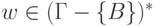 , остальная часть ленты
содержит пустые символы. Обозначим конфигурацию
машины Тьюринга как
, остальная часть ленты
содержит пустые символы. Обозначим конфигурацию
машины Тьюринга как 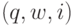 , где
, где  - текущее
состояние, i - выделенный элемент строки, "положение
головки" , w - текущее содержимое занятого участка ленты.
Если головка сдвигается с ячейки, машина должна записать
в нее символ, так что лента всегда состоит из участка,
состоящего из конечного числа непустых символов и
бесконечного количества пустых символов.
- текущее
состояние, i - выделенный элемент строки, "положение
головки" , w - текущее содержимое занятого участка ленты.
Если головка сдвигается с ячейки, машина должна записать
в нее символ, так что лента всегда состоит из участка,
состоящего из конечного числа непустых символов и
бесконечного количества пустых символов.
Шаг Tm определим следующим образом.
Пусть (q, A1, A2, ... An, i) - конфигурация Tm,
где  .
.
Если  и D(q, Ai) = (p, A, R)
и D(q, Ai) = (p, A, R)
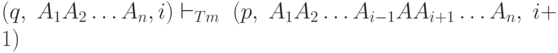
То есть Tm печатает символ A и передвигается вправо.
Если 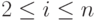 и
и 
( L от англ. Left), то если i = n, то допустимо A = B и

Tm печатает A и передвигается влево, но не за конец ленты.
Если i = n + 1, головка просматривает пустой символ B.
Если D(q, B) = (p, A, R), то 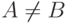 и
и

Если D(q, B) = (p, A, L), то допустимо A=B и
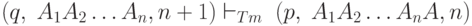
Если две конфигурации связаны отношением 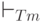 , то мы
говорим, что вторая получается из первой за один шаг. Если
вторая получается из первой за конечное, включая ноль,
число шагов, то такое отношение будем обозначать
, то мы
говорим, что вторая получается из первой за один шаг. Если
вторая получается из первой за конечное, включая ноль,
число шагов, то такое отношение будем обозначать  .
.
Язык, допускаемый Tm, это множество таких слов из T*, которые будучи расположены в левом конце ленты переводят Tm из начального состояния q0 с начальным положением головки в самом левом конце ленты в конечное состояние. Формально, язык, допускаемй Tm, это
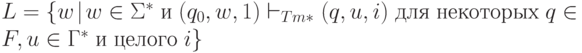
Если Tm распознает L, то Tm останавливается, то есть не имеет переходов после того, как слово допущено. Однако, если слово не допущено, возможно, что Tm не останавливается.
Язык, допускаемый некоторой Tm, называется рекурсивно перечислимым. Если Tm останавливается на всех входах, то говорят, что Tm задает алгоритм и язык называется рекурсивным.
Существует машина Тьюринга, которая по некоторому описанию произвольной Tm и кодированию слова x моделирует поведение Tm со входом x. Такая машина Тьюринга называется универсальной машиной Тьюринга.
Неразрешимость проблемы останова
Проблема останова для машины Тьюринга формулируется следующим образом: можно ли определить по данной машине Тьюринга в произвольной конфигурации со строкой конечной длины непустых символов на ленте остановится ли она? Говорят, что эта проблема рекурсивно неразрешима, что означает, что не существует алгоритма, который для любой Tm в произвольной конфигурации определял бы остановится ли в конце концов Tm.
Перенумеруем все машины Тьюринга и все возможные
входы над алфавитом 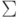 . Рассмотрим язык
. Рассмотрим язык
L1={xi|xi не допускается Ti}
Ясно, что 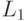 не допускается никакой Tm. Допустим, что
это не так. Пусть
не допускается никакой Tm. Допустим, что
это не так. Пусть 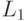 допускается Tj. Тогда
допускается Tj. Тогда  тогда
и только тогда, когда
тогда
и только тогда, когда 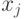 не допускается
не допускается 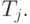 Но поскольку
Но поскольку 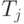 допускает
допускает 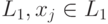 тогда и только тогда, когда допускается
тогда и только тогда, когда допускается 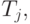 - противоречие. Так что
- противоречие. Так что 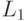 - не является рекурсивно перечислимым множеством.
- не является рекурсивно перечислимым множеством.


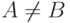 и)
и)