НОУ ИНТУИТ | Теория и практика параллельных вычислений. Лекция 11: Параллельные методы решения дифференциальных уравнений в частных производных

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 28.07.2007 | Доступ: свободный | Студентов: 2042 / 513 | Оценка: 4.53 / 4.26 | Длительность: 25:10:00

ISBN: 978-5-9556-0096-3

Темы: Программирование, Суперкомпьютерные технологии

Специальности: Программист

|

Вам нравится? Нравится 23 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В лекции рассматриваются вопросы организации параллельных вычислений для решения задач, в которых при математическом моделировании используются дифференциальные уравнения в частных производных. Для численного решения подобных задач обычно применяется метод конечных разностей (метод сеток), обладающий высокой вычислительной трудоемкостью. В лекции последовательно разбираются возможные способы распараллеливания сеточных методов на многопроцессорных вычислительных системах с общей и распределенной памятью. При этом большое внимание уделяется проблемам, возникающим при организации параллельных вычислений, анализу причин появления таких проблем и нахождению путей их преодоления. Для наглядной демонстрации излагаемого материала в качестве учебного примера рассматривается проблема численного решения задачи Дирихле для уравнения Пуассона

Ключевые слова: задача Дирихле, алгоритм Гаусса – Зейделя, мультипроцессор, разделяемая переменная, вычислительный эксперимент, ускорение, замедленные вычисления, алгоритм Гаусса, эффективность, однозначность результата, метод Якоби, система с распределенной памятью, операции передачи данных, MPI, каскадная схема, последовательный анализ, взаимоблокировка

Дифференциальные уравнения в частных производных представляют собой широко применяемый математический аппарат при разработке моделей в самых разных областях науки и техники. К сожалению, явное решение этих уравнений в аналитическом виде оказывается возможным только в частных простых случаях, и, как результат, возможность анализа математических моделей, построенных на основе дифференциальных уравнений, обеспечивается при помощи приближенных численных методов решения.

Объем выполняемых при этом вычислений обычно является значительным, и использование высокопроизводительных вычислительных систем традиционно для данной области вычислительной математики.

Проблематика численного решения дифференциальных уравнений в частных производных является областью интенсивных исследований.

Рассмотрим в качестве учебного примера проблему численного решения задачи Дирихле для уравнения Пуассона, которая определяется как задача нахождения функции u=u(x,y), удовлетворяющей в области определения D уравнению

$\left\{ \begin{aligned} & \frac{\partial^2u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}= f(x,y), & (x,y) \in D, \\ & u(x,y) = g(x,y), & (x,y) \in D^0, \end{aligned} \right.$

и принимающей значения g(x,y) на границе D⁰ области D ( f и g являются функциями, задаваемыми при постановке задачи). Подобная модель может применяться для описания установившегося течения жидкости, стационарных тепловых полей, процессов теплопередачи с внутренними источниками тепла и деформации упругих пластин. Данный пример часто используется в качестве учебно-практической задачи при изложении возможных способов организации эффективных параллельных вычислений (см. [ [ 12 ] , [ 60 ] ]).

Для простоты изложения материала в качестве области задания D функции u(x,y) далее будет использоваться единичный квадрат

$D=\{ (x,y)\in D:0\le x,y\le 1\}$

11.1. Последовательные методы решения задачи Дирихле

Одним из наиболее распространенных подходов к численному решению дифференциальных уравнений является метод конечных разностей ( метод сеток ) (см., например, [ [ 6 ] , [ 13 ] , [ 60 ] ]). Следуя этому подходу, область решения D можно представить в виде дискретного (как правило, равномерного) набора ( сетки ) точек ( узлов ). Так, например, прямоугольная сетка в области D может быть задана в виде (рис. 11.1)

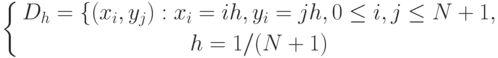
$\left\{ \begin{gathered} D_h=\{(x_i,y_j):x_i=ih, y_i=jh, 0\le i, j\le N+1, \\ h=1/(N+1) \end{gathered} \right.$

где величина N задает количество внутренних узлов по каждой из координат области D.

Обозначим оцениваемую при подобном дискретном представлении аппроксимацию функции u(x,y) в точках (xi, yj) через u_ij. Тогда, используя пятиточечный шаблон (см. рис. 11.1) для вычисления значений производных, мы можем представить уравнение Пуассона в конечно-разностной форме

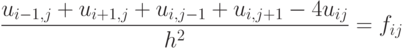
$\frac{u_{i-1,j}+u_{i+1,j}+u_{i,j-1}+u_{i,j+1}-4u_{ij}}{h^2} = f_{ij}$

Данное уравнение может быть разрешено относительно u_ij:

u_ij=0,25(u_i-1,j+u_i+1,j+u_i,j-1-h²f_ij).

Разностное уравнение, записанное в подобной форме, позволяет определять значение u_ij по известным значениям функции u(x,y) в соседних узлах используемого шаблона. Данный результат служит основой для построения различных итерационных схем решения задачи Дирихле, в которых в начале вычислений формируется некоторое приближение для значений u_ij, а затем эти значения последовательно уточняются в соответствии с приведенным соотношением. Так, например, метод Гаусса – Зейделя для проведения итераций уточнения использует правило

$u_{ij}^k=0,25(u_{i-1,j}^k + u_{i+1,j}^{k-1}+u_{i,j-1}^{k}+u_{i,j+1}^{k-1}-h^2 f_{ij})$

по которому очередное k -е приближение значения u_ij вычисляется по последнему k -му приближению значений u_i-1,j и u_i,j-1 и предпоследнему (k-1) -му приближению значений u_i+1,j и u_i,j+1. Выполнение итераций обычно продолжается до тех пор, пока получаемые в результате итераций изменения значений u_ij не станут меньше некоторой заданной величины ( требуемой точности вычислений ). Сходимость описанной процедуры (получение решения с любой желаемой точностью) является предметом всестороннего математического анализа (см., например, [ [ 6 ] , [ 13 ] , [ 60 ] ]), здесь же отметим, что последовательность решений, получаемых методом сеток, равномерно сходится к решению задачи Дирихле, а погрешность решения имеет порядок h².

Прямоугольная сетка в области D (темные точки представляют внутренние узлы сетки, нумерация узлов в строках слева направо, а в столбцах — сверху вниз)

Рис. 11.1. Прямоугольная сетка в области D (темные точки представляют внутренние узлы сетки, нумерация узлов в строках слева направо, а в столбцах — сверху вниз)

Рассмотренный алгоритм (метод Гаусса – Зейделя) на псевдокоде, приближенном к алгоритмическому языку С++, может быть представлен в виде:

Алгоритм 11.1. Последовательный алгоритм Гаусса – Зейделя

// Алгоритм 11.1
do {
  dmax = 0; // максимальное изменение значений u
  for ( i=1; i<N+1; i++ )
    for ( j=1; j<N+1; j++ ) {
      temp = u[i][j];
      u[i][j] = 0.25*(u[i-1][j]+u[i+1][j]+
                u[i][j-1]+u[i][j+1]–h*h*f[i][j]);
      dm = fabs(temp-u[i][j]);
      if ( dmax < dm ) dmax = dm;
    }
} while ( dmax > eps );

(напомним, что значения u_ij при индексах i,j=0,N+1 являются граничными, задаются при постановке задачи и не изменяются в ходе вычислений).

Рис. 11.2. Вид функции u(x,y) в примере для задачи Дирихле

Для примера на рис. 11.2 приведен вид функции u(x,y), полученной для задачи Дирихле при следующих граничных условиях:

$\left\{ \begin{aligned} &\quad f(x,y)=0, \quad (x,y) \in D, \\ &\quad 100-200x, \quad y=0, \\ &\quad 100-200x, \quad x=0, \\ &-100+200x, \quad y=1, \\ &-100+200x, \quad x=1. \\ \end{aligned} \right.$

Общее количество итераций метода Гаусса – Зейделя составило 210 при точности решения eps=0,1 и N=100 (в качестве начального приближения величин u_ij использовались значения, сгенерированные датчиком случайных чисел из диапазона [-100, 100]).

Дальше >>

Авторизоваться

Теория и практика параллельных вычислений

Параллельные методы решения дифференциальных уравнений в частных производных

11.1. Последовательные методы решения задачи Дирихле

Вопросы и ответы