Основы машинной графики

Математические основы компьютерной графики

Для того чтобы отображать графические объекты на дисплее нужно иметь некий инструмент, позволяющий легко и просто описывать эти объекты на языке математики. Положение точек на плоскости очень удобно описывать с помощью декартовой системы координат. Чтобы создать декартову систему координат нужно провести две прямые неколлинеарные линии, которые называют осями. Пусть они пересекаются в точке O, которую называют началом координат. Выберем на построенных осях единицу измерения. Тогда положение любой точки плоскости можно описать через координаты этой точки, которые представляют собой расстояния от начала координат до проекций точки на соответствующие оси координат. Проекцией точки на координатную ось называется точка пересечения прямой, проходящей через заданную точку и параллельной другой оси координат. Вообще введенные оси координат могут располагаться под произвольным углом (рис. 1.1).

Рис. 1.1.

Однако, на практике удобно пользоваться системой координат со взаимно перпендикулярными осями. Такая система координат называется ортогональной. Оси координат имеют названия; горизонтальная ось называется осью абсцисс ( Ox ), вертикальная – осью ординат ( Oy ). Таким образом, точка на плоскости представляется двумя своими координатами, что записывается в виде двумерного вектора P=(x,y).

Математический аппарат описания точек на плоскости с помощью декартовой системы координат идеально подходит для выполнения различных аффинных преобразований над точками (сдвиг, масштабирование, вращение).

Точку P(x,y), заданную на плоскости можно перенести (сдвинуть) в новую позицию путем добавления к координатам этой точки констант переноса. Для произвольной точки P=(x,y), которая перемещается в новую точку P'=(x',y'), сдвигаясь на Tx единиц параллельно оси абсцисс и на Ty единиц параллельно оси ординат, можно записать следующие выражения: x'=x+Tx, y'=y+Ty. Так, например, точка с координатами P(1,2) смещаясь на расстояние (5,7) преобразуется в точку P'(6,9). Определяя точку и перенос как вектор-строки P=(x,y), P'=(x',y') и T=(Tx,Ty) можно записать преобразование переноса (сдвига) в векторной форме: (x',y')=(x,y)+(Tx,Ty) или P'=P+T. Преобразованию можно подвергнуть не только одни точки. Геометрический объект можно переместить, применив к каждой его точке преобразование переноса. Так, если в описании объекта имеются отрезки прямой, то достаточно применить преобразование к концам отрезка и затем провести прямую линию между двумя преобразованными точками. Это правило справедливо и для операций масштабирования и поворота. На рис. 1.2 представлен результат действия на треугольник операции переноса на расстояние (2,-1).

Рис. 1.2.

Точки можно подвергнуть операции масштабирования (растяжения или сжатия) в Sx раз вдоль оси абсцисс и в Sy раз вдоль оси ординат. Полученные в результате новые точки будут выражаться как: x'=x*Sx ; y'=y*Sy. Определив S как

Рис. 1.3.

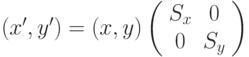
Следует отметить, что операция масштабирования производится относительно начала координат. В результате преобразования объект может стать меньше/больше в размерах и ближе/дальше от начала координат. Пропорции объекта также могут измениться при масштабировании с различными коэффициентами: . Для сохранения пропорций необходимо, чтобы масштабные коэффициенты были равны: Sx=Sy.

Точка плоскости P=(x,y) может быть повернута на произвольный угол относительно начала координат и перейдет в новую точку P'=(x',y') (рис. 1.4)

Рис. 1.4.

Выведем формулы для пересчета точки (x,y) в точку (x',y'). Обозначим расстояние от начала координат до точки P(x,y) через 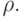Очевидно, что расстояние от начала координат до точки P'(x',y') также будет 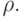Пусть Q и Q' - проекции точек P и P' соответственно на ось абсцисс. Тогда из прямоугольного треугольника OP'Q' и тригонометрических определений синуса и косинуса имеем:

Домножим правую и левую части уравнений на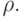

Используя простейшие тригонометрические свойства прямоугольного треугольника OPQ, следует заметить, что , а . Таким образом, формула "перевода" точки P(x,y) в точку P'(x',y') поворотом на угол относительно начала координат будет:

В матричном виде преобразование вращения будет выглядеть так:

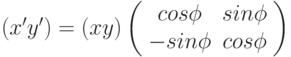
Так треугольник с координатами вершин (20,0),(60,0),(40,100) после поворота на угол 45 градусов по часовой стрелке относительно начала координат градусов будет иметь новые значения координат вершин: .

Точка плоскости P(x,y) может быть легко отражена относительно прямых y=0, x=0, y=x следующим образом. Отражение относительно прямой y=0 (ось абсцисс) может быть получено с использованием матрицы 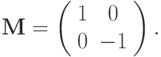Так, например, точка P=(2,3) при таком отражении преобразуется в точку (рис. 1.5).

Подобным образом матрица отражения относительно прямой x=0 (ось ординат) будет иметь вид 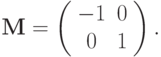Точка P=(2,3) при отражении относительно оси ординат преобразуется в точку (рис. 1.5).

Отражение относительно прямой y=x осуществляется с помощью матрицы Точка P=(2,3) в результате такого отражения преобразуется в точку (рис. 1.5).

Рис. 1.5.

Рассмотренные выше аффинные преобразования переноса, масштабирования, вращения и отражения можно записать в матричной форме следующим образом: P'=P+T, P'=P*S, P'=P*R, P'=P*M, где P' - координаты преобразованной точки, P - координаты исходной точки, T - вектор сдвига ( translate ), S - матрица масштабирования ( scale ), R - матрица вращения ( rotate ), M - матрица отражения ( mirror ). К сожалению, операция переноса (сдвига) реализуется отдельно (с помощью сложения) от масштабирования, поворота и отражения (с помощью умножения). Тем не менее, существует возможность, чтобы все эти элементарные преобразования (перенос, масштабирование, вращение, отражение) можно было реализовать с помощью только операций умножения матриц. Данная возможность реализуется с помощью так называемых однородных координат точки.