НОУ ИНТУИТ | Практикум по методам построения алгоритмов. Лекция 1: Переменные, выражения, присваивания

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 08.04.2009 | Доступ: свободный | Студентов: 485 / 0 | Длительность: 17:26:00

Темы: Программирование, Алгоритмы и дискретные структуры, Образование

Специальности: Программист

|

Вам нравится? Нравится 24 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

1.3.Индуктивные функции (по А. Г. Кушниренко)

Пусть M - некоторое множество. Функция f, аргументами которой являются последовательности элементов множества M, а значениями - элементы некоторого множества N, называется индуктивной, если ее значение на последовательности $x[1]\ldots x[n]$ можно восстановить по ее значению на последовательности $x[1]\ldots x[n-1]$ и по x[n], то есть если существует функция $F\colon N\times M \to N$ , для которой

$f(\langle x[1],\ldots,x[n]\rangle) = F(\, f(\langle x[1],\ldots,x[n-1]\rangle),x[n]).$

Например, функция sum (сумма всех членов последовательности) индуктивна, поскольку очередной член последовательности прибавляется к ее сумме:

$sum(\langle x[1],\ldots,x[n]\rangle) = sum(\langle x[1],\ldots,x[n-1]\rangle)+x[n].$

Другой пример индуктивной функции - длина последовательности. В этом случае F(n,m)=n+1

.

Напротив, среднее арифметическое не является индуктивной функцией: если мы знаем среднее арифметическое некоторой последовательности, но не знаем ее длины, то не можем предсказать, каким станет среднее арифметическое после дописывания некоторого (известного нам) числа.

Схема алгоритма вычисления индуктивной функции:

k := 0; f := f0; 
{инвариант: f - значение функции на < x[1],...,x[k] > } 
while  k<>n do begin 
| k := k + 1; 
| f := F (f, x[k]); 
end;

Здесь f0 - значение функции на пустой последовательности (последовательности длины 0 ). Если функция f определена только на непустых последовательностях, то первая строка заменяется на

k:=1; f:=f(< x[1] > );

Индуктивные расширения.

Если функция f не является индуктивной, полезно искать ее индуктивное расширение - такую индуктивную функцию g, значения которой определяют значения f (это значит, что существует такая функция t, что

$f (\langle x[1]\ldots x[n]\rangle) = t (g(\langle x[1]\ldots x[n]\rangle))$

при всех $\langle x[1] \ldots x[n]\rangle$ ). Можно доказать, что среди всех индуктивных расширений существует минимальное расширение F (минимальность означает, что для любого индуктивного расширения g значения F определяются значениями g ).

1.3.1. Указать индуктивные расширения для следующих функций:

(а) среднее арифметическое последовательности вещественных чисел;

(б) число элементов последовательности целых чисел, равных ее максимальному элементу;

(в) второй по величине элемент последовательности целых чисел (тот, который будет вторым, если переставить члены в неубывающем порядке);

(г) максимальное число идущих подряд одинаковых элементов;

(д) максимальная длина монотонного (неубывающего или невозрастающего) участка из идущих подряд элементов в последовательности целых чисел;

(е) число групп из единиц, разделенных нулями (в последовательности нулей и единиц).

Решение.

(а) $\langle$ сумма всех членов последовательности; длина $\rangle$ ;

(б) $\langle$ число элементов, равных максимальному; значение максимального $\rangle$ ;

(в) $\langle$ наибольший элемент последовательности; второй по величине элемент $\rangle$ ;

(г) $\langle$ максимальное число идущих подряд одинаковых элементов; число идущих подряд одинаковых элементов в конце последовательности; последний элемент последовательности $\rangle$ ;

(д) $\langle$ максимальная длина монотонного участка; максимальная длина неубывающего участка в конце последовательности; максимальная длина невозрастающего участка в конце последовательности; последний член последовательности $\rangle$ ;

(е) $\langle$ число групп из единиц, последний член $\rangle$ .

1.3.2. (Сообщил Д. В. Варсанофьев) Даны две последовательности целых чисел $x[1]\ldots x[n]$ и $y[1]\ldots y[k]$ . Выяснить, является ли вторая последовательность подпоследовательностью первой, то есть можно ли из первой вычеркнуть некоторые члены так, чтобы осталась вторая. Число действий порядка n+k .

Решение. Вариант 1. Будем сводить задачу к задаче меньшего размера.

n1:=n; 
k1:=k; 
{инвариант: искомый ответ <=> возможность из x[1]..x[n1] 
   получить y[1]..y[k1] } 
while (n1 > 0) and (k1 > 0) do begin 
| if x[n1] = y[k1] then begin 
| | n1 := n1 - 1; 
| | k1 := k1 - 1; 
| end else begin 
| | n1 := n1 - 1; 
| end; 
end; 
{n1 = 0 или k1 = 0; если k1 = 0, то ответ - да, если k1<>0 
 (и n1 = 0), то ответ - нет} 
answer := (k1 = 0);

Мы использовали то, что если x[n1]=y[k1] и $y[1]\ldots y[k1]$ - подпоследовательность $x[1]\ldots x[n1]$ , то $y[1]\ldots y[k1-1]$ - подпоследовательность $x[1]\ldots x[n1-1]$ .

Вариант 2. Функция $\langle x[1]\ldots x[n1]\rangle$ $\mapsto$ [максимальное k1, для которого $y[1]\ldots y[k1]$ есть подпоследовательность $x[1]\ldots x[n1]$ ] индуктивна.

1.3.3. Даны две последовательности $x[1]\ldots x[n]$ и $y[1]\ldots y[k]$ целых чисел. Найти максимальную длину последовательности, являющейся подпоследовательностью обеих последовательностей. Количество операций порядка $n\cdot k$ .

Решение (сообщено М. Н. Вайнцвайгом, А. М. Диментманом). Обозначим через 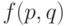f(p,q) максимальную длину общей подпоследовательности последовательностей $x[1]\ldots x[p]$ и $y[1]\ldots y[q]$ . Тогда

$\begin{eqnarray*} x[p]\ne y[q] &\! \Rightarrow\!& f(p,q) = \max\,(f(p,q\!-\!1), f(p\!-\!1,q)); \\ x[p]=y[q] &\! \Rightarrow\! &f(p,q) = \max\,(f(p,q\!-\!1), f(p\!-\!1,q), f(p\!-\!1,q\!-\!1)\!+\!1); \end{eqnarray*}$

(Поскольку $f(p-1,q-1)+1 \ge f(p,q-1), f(p-1,q)$ , во втором случае максимум трех чисел можно заменить на третье из них.) Поэтому можно заполнять таблицу значений функции f, имеющую размер $n\cdot k$ . Можно обойтись и памятью порядка k (или n ), если индуктивно (по p ) вычислять $\langle f(p,0),\ldots,f(p,k)\rangle$ (как функция от p этот набор индуктивен ).

1.3.4. (из книги Д. Гриса) Дана последовательность целых чисел $x[1],\ldots,x[n]$ . Найти максимальную длину ее возрастающей подпоследовательности (число действий порядка $n\,log n$ ).

Решение. Искомая функция не индуктивна, но имеет следующее индуктивное расширение: в него входят помимо максимальной длины возрастающей подпоследовательности (обозначим ее k ) также и числа $u[1],\ldots,u[k]$ , где u[i] - минимальный из последних членов возрастающих подпоследовательностей длины i. Очевидно, $u[1]\le\ldots\le u[k]$ . При добавлении нового члена в x значения u и k корректируются.

n1 := 1; k := 1; u[1] := x[1]; 
{инвариант: k и u соответствуют данному выше описанию} 
while n1 <> n do begin 
| n1 := n1 + 1; 
| ... 
| {i - наибольшее из тех чисел отрезка 1..k, для 
|   которых u[i] < x[n1]; если таких нет, то i=0 } 
| if i = k then begin 
| | k := k + 1; 
| | u[k+1] := x[n1]; 
| end else begin {i < k, u[i] < x[n1] <= u[i+1] } 
| | u[i+1] := x[n1]; 
| end; 
end;

Фрагмент ... использует идею двоичного поиска; в инварианте условно полагаем u[0] равным минус бесконечности, а u[k+1] - плюс бесконечности. Наша цель: $u[i] < x[n1]\le u[i+1]$ .

i:=0; j:=k+1; 
{u[i] < x[n1] <= u[j], j > i} 
while (j - i) <> 1 do begin 
| s := i + (j-i) div 2;    {i < s < j} 
| if x[n1] <= u[s] then begin 
| | j := s; 
| end else begin {u[s] < x[n1]} 
| | i := s; 
| end; 
end; 
{u[i] < x[n1] <= u[j], j-i = 1}

Замечание. Более простое (но не минимальное) индуктивное расширение получится, если для каждого i хранить максимальную длину возрастающей подпоследовательности, оканчивающейся на x[i]. Это расширение приводит к алгоритму с числом действий порядка 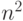n^2 . Есть и другой изящный алгоритм с квадратичным временем работы (сообщил М. В. Вьюгин): найти максимальную общую подпоследовательность исходной последовательности и отсортированной последовательности с помощью предыдущей задачи.

1.3.5. Какие изменения нужно внести в решение предыдущей задачи, если надо искать максимальную неубывающую последовательность?

Дальше >>

Авторизоваться

Практикум по методам построения алгоритмов

Переменные, выражения, присваивания

1.3.Индуктивные функции (по А. Г. Кушниренко)

Вопросы и ответы