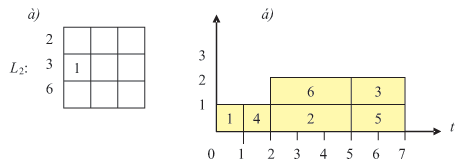Параллельное программирование — аппарат исследования операций
Решение задачи 2 распараллеливания для однородных ВС
Формулировка задачи: Для данного алгоритма, которому соответствует информационный граф G, найти минимальное время T и план выполнения этого алгоритма на данной однородной ВС, содержащей n процессоров.
Теорема. Для того, чтобы T было минимальным временем выполнения алгоритма, представленного информационным графом G = (X, P, Г), на однородной ВС, состоящей из n процессоров, необходимо и достаточно, чтобы T было наименьшей из возможных длин критических путей в графах вида G'= (X, P, Г'), что получены из данного объединением вершин, соответствующих работам каждого ПМВНР, который содержит r > n работ, r - n ориентированными дугами в n путей, не содержащих общих вершин.
Алгоритм 8 решения задачи 2 — нахождения графа-решения G'
- По алгоритму 5 находим оценку T = T0 минимального времени выполнения данного алгоритма на ВС, содержащей n процессоров.
- Опыт подсказывает, что в подавляющем большинстве случаев полученная оценка совпадает с минимальным временем выполнения алгоритма на данной ВС. Чтобы сократить объём вычислений, целесообразно с помощью алгоритма 6 решения задачи 1 установить, способны ли n процессоров выполнить данный алгоритм за время T0. Если T0 — не решение задачи 2, используем следующий метод.
- Полагаем
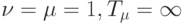 , где
, где  — заведомо большое число, например,
максимально допустимое на используемой ЭВМ.
— заведомо большое число, например,
максимально допустимое на используемой ЭВМ. -
Находим наименьшее значение
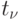 такое, что
такое, что 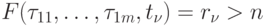 .
.Если такого значения
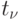 нет на первом же шаге сглаживания
плотности загрузки
(при
нет на первом же шаге сглаживания
плотности загрузки
(при  ), то значение Tкр — решение
задачи 2. Если такого значения больше
нет при
), то значение Tкр — решение
задачи 2. Если такого значения больше
нет при  , то увеличиваем значение
, то увеличиваем значение  на
единицу и полагаем
на
единицу и полагаем 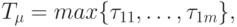 т.е. длине критического пути в графе G', построенном в соответствии с
условиями теоремы. Не меняя значение
т.е. длине критического пути в графе G', построенном в соответствии с
условиями теоремы. Не меняя значение  переходим к выполнению
6. (Если
переходим к выполнению
6. (Если  , то т.к. T0 — не решение задачи, искать
значение
, то т.к. T0 — не решение задачи, искать
значение  нецелесообразно,
т.е. найденное значение
нецелесообразно,
т.е. найденное значение  — решение задачи 2).
— решение задачи 2). -
Если значение
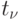 , обеспечивающее неравенство в пункте 4,
найдено, выделяем
множество работ
, обеспечивающее неравенство в пункте 4,
найдено, выделяем
множество работ  ,
для которых
,
для которых .
.Множество
 является подмножеством некоторого ПМВНР.
является подмножеством некоторого ПМВНР. - Введём очередную, ещё не испытанную комбинацию
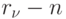 связей, как указано
в теореме, так, чтобы длина критического пути в полученном при этом графе G' была меньше
связей, как указано
в теореме, так, чтобы длина критического пути в полученном при этом графе G' была меньше  .
. - Если такая комбинация связей существует, увеличиваем
 на единицу, уточняем
новые значения
на единицу, уточняем
новые значения  , переходим к
выполнению 4.
, переходим к
выполнению 4. - Если такой комбинации связей не существует или все они уже перебраны и
при
этом
 , уменьшаем
, уменьшаем  на единицу и
переходим к 6. Если же испытаны все
комбинации связей при
на единицу и
переходим к 6. Если же испытаны все
комбинации связей при  , то последнее значение
, то последнее значение  определяет искомое
определяет искомое  .
.
Конец алгоритма.
Пример. Пусть заданы 6 задач (m = 6), заданы их частичная упорядоченность графом G, заданы времена решения (веса вершин). Требуется найти расписание выполнения этих задач на двух процессорах (n = 2) — такое, чтобы время решений этих задач было минимальным.
Найдём нижнюю оценку длины расписания T.
Первоначально полагаем ![T = \max \left \{ \left]
\frac{1}{n}\suml_{j=1}^m t_j
\right [, \,T_\text{кр} \right \} = {\max \{ 6,6 \} = 6}](/sites/default/files/tex_cache/27687f5812acca386ca173e6e1e6df2e.png) .
.
По алгоритму 6, испытывая значения функции минимальной загрузки, найдём, что  . Произведем
единственное уточнение значения
. Произведем
единственное уточнение значения ![T_0 = 6 + \left]\frac{1}{2}(\frac{11}{5}-2)\right [=7](/sites/default/files/tex_cache/300403ed515f1087f217f7feb889fd6e.png) .
.
Без учета реально доступного количества процессоров составим (рис. 7.23) временную диаграмму решения всей совокупности задач — такую, при которой каждая из задач решается как можно раньше, и определим загрузку как бы неограниченного числа процессоров:
-
находим первый момент времени, при котором по этой диаграмме нам требуется более двух процессоров: при t=1 это количество F(1)=3. Выделим образующие это значение F задачи: {2, 3, 4} и составим матрицу L1 (рис. 7.24а). Первой испытываемой связью является связь 3 -> 2. Диаграмма, соответствующая этой связи, — на рис. 7.24б.
Т.к. больше нет значений функции плотности загрузки, превышающих 2, то мы предполагаем возможное решение, но продолжаем перебор связей для поиска более короткого расписания.
-
следующей испытываемой связью по матрице L1, определяющей длину критического пути, меньшую 8, является связь 4 -> 2. Соответствующее расписание — на рис. 7.25.
-
вновь находим первый момент времени, при котором нам требуется более двух процессоров: при t = 2 это количество F(2) = 3. Выделим образующие это значение F задачи: {2, 3, 6} и составим матрицу L2 (рис. 7.26а). Первой возможной связью, не приводящей к длине критического пути, равной 8 или выше, является связь 2 -> 3. Диаграмма, соответствующая этой связи, — на рис. 7.26б.
Т.к. значение функции плотности загрузки больше не превышает значение 2, то мы нашли оптимальное расписание, ибо его длина не превосходит нижней оценки — значения 7.
Задачи точного распараллеливания в настоящей лекции освещаются только для однородных систем исполнителей, когда все такие исполнители "умеют" всё и каждую работу выполняют за одинаковое время. Это предполагает применение методов для однородных вычислительных систем. Однако при более широком применении методов распараллеливания в управлении и экономике актуальна постановка этих задач для неоднородного состава исполнителей, в частности — когда исполнители обладают разной специализацией. Достаточно рассмотреть управление строительством или уборочной кампанией. Алгоритмы точного решения задач распараллеливания для неоднородных систем представлены в [3].