Лекция 5: Параллельные методы расчета транспортной сети

Введем линейный массив переменных x_ij = y_k, где k = (i - 1)n + j.

Исключим из рассмотрения последнее уравнение. Система уравнений граней (действительных и возможных) многогранника решений примет вид

y₁ + y₂ + y₃ + y₄ = 11

y₅ + y₆ + y₇ + y₈ = 11

y₉ + y₁₀ + y₁₁ + y₁₂ = 8 (5.7)

y₁+y₅+ y₉=5

y₂+y₆+y₁₀ = 9

y₃+ y₇+ y₁₁ = 9

y_k = 0, k = 1, 2, ... , 12.

Итак, на первом этапе задача свелась к выбору и анализу комбинаций по 12 - 6 = 6 нулевых значений координат искомой вершины многогранника решений. Выполняя подстановку выбранной комбинации в (5.7), мы можем решить образовавшуюся систему шести уравнений с шестью неизвестными. Таким образом, мы сможем найти координаты некоторой вершины.

Комбинации по шесть нулевых значений координат ("комбинации нулей") следует выбирать так, чтобы не обратилась в нуль левая часть хотя бы одного уравнения (5.7), включая исключенное уравнение. Например, комбинация, где y₁ = y₂ = y₃ = y₄ = 0, недопустима.

Найдем дополнительные контрольные ограничения: чтобы решение было не отрицательным, необходимо, чтобы любое значение y_k, k = 1, ... , m x n, не превышало значение y_k — величины правой части того уравнения, в котором оно участвует.

Тогда в нашем примере y₁ <= min(11, 5) =y₁ = 5, аналогично y₂ <= y₂ = 9, y₃ <= y₃ = 9, y₄ <= y₄ = 7, y₅ <= y₅ = 5, y₆ <= y₆ = 9, y₇ <= y₇ = 9, y₈ <= y₈ =7, y₉ <= y₉ = 5, y₁₀ <= y₁₀ = 8, y₁₁ <=y₁₁ = 8, y₁₂ <= y₁₂ = 7. Здесь при оценке y₄, y₈, y₁₂ учтено последнее уравнение в (5.6).

Воспользуемся векторной формой представления, чтобы подготовить удобные, нетрудоемкие матричные преобразования. А именно, наша система m + n - 1 линейных уравнений-ограничений имеет вид

AY = B,

где A — нуль-единичная матрица, Y — столбец переменных, B — столбец свободных членов:

( 5.8)

Тогда для нахождения хотя бы одного допустимого решения выберем допустимую комбинацию нулей по следующему алгоритму:

1. Положим l = 0.
2. Положим l := l + 1, y_l = 0. Исключим из матрицы A столбец, соответствующий этой переменной.
3. Проверяем, появилась ли в A строка, содержащая только нулевые элементы, или обратилась ли в нуль левая часть исключенного уравнения. (Предполагаем, что все свободные члены уравнений больше нуля.) При положительном результате анализа выполняем шаг 5. В противном случае — следующий шаг.
4. Для каждой s -й строки A выделяем множество {y_s} переменных, соответствующих единичным элементам. Проверяем: 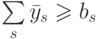?При отрицательном результате анализа (свободный член превышает сумму верхних оценок переменных) выполняем шаг 5. В случае успешной проверки 3 и 4 выполняем шаг 6.
5. Данный шаг выполняется, если испытываемое значение y_l = 0 выбрано неудачно. Отменяем исключение столбца, соответствующего переменной y_l, и выполняем шаг 2.
6. Фиксируем y_l = 0, и если комбинация нулей сформирована не полностью, выполняем шаг 2.

Продолжим рассмотрение примера.

Полагаем y₁ = 0. Это не приводит к нарушению оценок, указанных в алгоритме.

Полагаем y₂ = 0. Это также не приводит к нарушению оценок.

Полагаем y₃ = 0. Нулевые строки не появились. Однако в первой строке осталась единственная единица, соответствующая переменной y₄. Т.к. y₄= 7 < 11, отвергаем нулевое значение переменной.

Полагаем y₄ = 0. Нулевые строки не появились, однако в первой же строке осталась единственная единица, соответствующая переменной y₃. Т.к. y₃ = 9 < 11, отвергаем и это значение.

Полагаем y₅ = 0. Это не приводит к нарушению оценок.

Полагаем y₆ = 0. В пятой строке остается единственная единица, соответствующая y₁₀. Т.к. y₁₀ = 8 < 9, отвергаем нулевое значение переменной.

Полагаем y₇ = 0, что не приводит к нарушению оценок.

Значение y₈ = 0 приводит к нарушению оценки во втором уравнении.

Значение y₉ = 0 приводит к появлению нулевой строки.

Значение y₁₀ = 0 не приводит к нарушению оценок.

Значение y₁₁ = 0 также не приводит к нарушению оценок.

Итак, комбинация нулей найдена. Это отмеченные в (5.8) значения

y₁ = 0, y₂ = 0, y₅ = 0, y₇ = 0, y₁₀ = 0, y₁₁ = 0. (5.9)