Функциональные зависимости и реляционные базы данных
Рассмотрим схему отношения R (город, адрес, почтовый_индекс). В этом случае существуют следующие нетривиальные, т.е. имеющие смысл в контексте предметной области, ФЗ город, адрес -> почтовый_индекс (полный адрес определяет почтовый индекс) и почтовый_индекс -> город (почтовый индекс определяет город, но не адрес). Легко убедиться, что оба множества атрибутов {город, адрес} и {адрес, почтовый_индекс} являются ключами отношения. Какой из них выбрать, решает проектировщик базы данных.
Для того чтобы определить ключи отношений и логические следствия ФЗ для заданной схемы отношения, необходимо вычислить F+ или для заданного F уметь определять, принадлежит ли данная ФЗ его замыканию F+. Для этого необходимо иметь набор правил - операций над ФЗ, позволяющих ими манипулировать.
Набор правил вывода должен быть полным, т.е. давать возможность вывести все зависимости из F+, и надежным, т.е. не позволять вывести зависимость из F, не принадлежащую F+. Таким образом, правила вывода, называемые также аксиомами вывода функциональных зависимостей, должны позволять вывести множество функциональных зависимостей, присущих рассматриваемой схеме отношения R(A1, A2, ..., Am) на заданном универсальном множестве атрибутов U по заданному множеству ФЗ F = {F1, F2, ..., Fk}.
Далее представлены восемь аксиом вывода функциональных зависимостей.
-
Рефлексивность. Если
 , то ФЗ
, то ФЗ 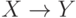 следует из F. Иначе
следует из F. Иначе  .
. - Пополнение. Если
 и задана ФЗ
и задана ФЗ 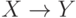 из F, то имеет место ФЗ
из F, то имеет место ФЗ  .
. -
Транзитивность. Если
 и задана ФЗ
и задана ФЗ  из F , то имеет место ФЗ
из F , то имеет место ФЗ  .
. - Расширение. Если
 и задана ФЗ
и задана ФЗ 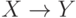 , то
, то 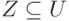 имеет место ФЗ
имеет место ФЗ 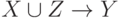 .
. - Продолжение. Если
 , и задана ФЗ
, и задана ФЗ 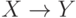 , то
, то  имеет место ФЗ
имеет место ФЗ  .
. - Псевдотранзитивность. Если
 , и заданы ФЗ
, и заданы ФЗ 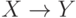 и ФЗ
и ФЗ  , то имеет место ФЗ
, то имеет место ФЗ  .
. - Аддитивность. Если
 , и заданы ФЗ
, и заданы ФЗ 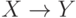 и ФЗ
и ФЗ  , то имеет место ФЗ
, то имеет место ФЗ  .
. - Декомпозиция. Если
 , и задана ФЗ
, и задана ФЗ 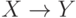 , то имеет мето ФЗ
, то имеет мето ФЗ  .
.
Пример. Определение ключа отношения с помощью правил вывода
Используя три первых аксиомы вывода, покажем, что пара атрибутов {адрес, почтовый_индекс} из примера выше являются ключом отношения (город, адрес, почтовый_индекс), иначе имеет место ФЗ адрес, почтовый_индекс -> город, адрес, почтовый_индекс. Задана ФЗ: почтовый_индекс -> город. Используя аксиому пополнения, пополним эту ФЗ атрибутом адрес, получаем адрес, почтовый_индекс -> город, адрес. Задана ФЗ город, адрес -> почтовый_индекс. Используя аксиому пополнения, пополнив эту ФЗ атрибутами город, адрес, получим город, адрес -> город, адрес, почтовый_индекс. Тогда по аксиоме транзитивности получаем адрес, почтовый_индекс -> город, адрес, почтовый_индекс.
Можно доказать утверждение о том, что настоящие правила вывода позволяют по заданному множеству ФЗ F построить все зависимости, допускаемые на U. Таким образом, система правил вывода ФЗ 1-6 является надежной и полной.
Покажем, как можно доказать утверждение о полноте и надежности аксиом вывода. Аксиомы 1, 2 и 3 составляют независимое подмножество среди всех шести аксиом и называются аксиомами Армстронга. Из них можно вывести все остальные аксиомы. Поэтому надежность и полноту достаточно установить только для первых трех аксиом.
Надежность аксиом заключается в том, что если ФЗ  выведена из F с помощью этих аксиом, то она справедлива на любом отношении, на котором справедливы ФЗ из F. Аксиома рефлексивности является надежной, так как нельзя иметь отношение R с двумя кортежами, которые совпадают по Х, но не совпадают по некоторому его подмножеству. Для доказательства аксиомы пополнения предположим, что имеется отношение R и справедлива ФЗ
выведена из F с помощью этих аксиом, то она справедлива на любом отношении, на котором справедливы ФЗ из F. Аксиома рефлексивности является надежной, так как нельзя иметь отношение R с двумя кортежами, которые совпадают по Х, но не совпадают по некоторому его подмножеству. Для доказательства аксиомы пополнения предположим, что имеется отношение R и справедлива ФЗ  на R. Однако есть два кортежа t и s, которые совпадают по атрибутам XZ, но не совпадают по YZ. Поскольку они не могут совпадать по какому-либо атрибуту из Z, то они не должны совпадать по некоторому атрибуту из Y. Тогда они совпадают по X, но не совпадают по Y, что противоречит существованию ФЗ
на R. Однако есть два кортежа t и s, которые совпадают по атрибутам XZ, но не совпадают по YZ. Поскольку они не могут совпадать по какому-либо атрибуту из Z, то они не должны совпадать по некоторому атрибуту из Y. Тогда они совпадают по X, но не совпадают по Y, что противоречит существованию ФЗ  . Надежность аксиомы транзитивности уже была доказана в настоящем
учебном элементе ранее.
. Надежность аксиомы транзитивности уже была доказана в настоящем
учебном элементе ранее.
Для доказательства полноты аксиом вывода введем понятие замыкания множества атрибутов X относительно множества ФЗ F.
Определение 10. Пусть F - множество ФЗ на множестве атрибутов U и
. Тогда замыканием X+ множества ФЗ F называется множество атрибутов А, таких, что ФЗ
может быть выведена из F по аксиомам 1-3.
Нетрудно показать, что ФЗ  следует из аксиом 1-3 тогда и только тогда, когда
следует из аксиом 1-3 тогда и только тогда, когда  . По определению замыкания для каждого атрибута из Y выводится ФЗ
. По определению замыкания для каждого атрибута из Y выводится ФЗ  . По аксиоме объединения имеет место ФЗ
. По аксиоме объединения имеет место ФЗ  . Обратно, если выполняется ФЗ
. Обратно, если выполняется ФЗ  , то по аксиоме декомпозиции имеет место ФЗ
, то по аксиоме декомпозиции имеет место ФЗ 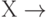 каждый атрибут из Y, и, следовательно, имеет место
каждый атрибут из Y, и, следовательно, имеет место  .
.
Теперь, для того чтобы показать полноту аксиом 1-3, покажем, что если при заданном F ФЗ  не может быть выведена из данных аксиом, то должно существовать такое отношение, в котором справедливы все ФЗ F, кроме ФЗ
не может быть выведена из данных аксиом, то должно существовать такое отношение, в котором справедливы все ФЗ F, кроме ФЗ  .
.
Рассмотрим отношение R с двумя кортежами:
Все зависимости из F справедливы на R. Следует показать, что  не удовлетворяется на R. Допустим обратное. Из
не удовлетворяется на R. Допустим обратное. Из  следует
следует  , иначе два кортежа, совпадая по Х, не совпадают по Y. Тогда ФЗ
, иначе два кортежа, совпадая по Х, не совпадают по Y. Тогда ФЗ  следует из аксиом 1-3, что приводит к противоречию. Таким образом, аксиомы 1-3 полны.
следует из аксиом 1-3, что приводит к противоречию. Таким образом, аксиомы 1-3 полны.
На основе аксиом вывода можно уточнить понятие замыкания множества ФЗ 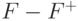 , как наименьшего множества, содержащего F, которое не может быть расширено за F с помощью аксиом 1, 2 и 3. Понятие замыкания является основным при доказательстве приведенного выше утверждения. Оно также важно при определении, имеет ли множество ФЗ F зависимость
, как наименьшего множества, содержащего F, которое не может быть расширено за F с помощью аксиом 1, 2 и 3. Понятие замыкания является основным при доказательстве приведенного выше утверждения. Оно также важно при определении, имеет ли множество ФЗ F зависимость  . Для этого достаточно проверить, принадлежит ли рассматриваемая зависимость множеству F+.
. Для этого достаточно проверить, принадлежит ли рассматриваемая зависимость множеству F+.
Вычисление замыкания конечного множества ФЗ является трудоемкой задачей, так как необходимо перебрать множество всех подмножеств, а таких множеств, как известно, 2n, где n - число элементов исходного множества. Однако вычислить замыкание X+ для данного множества атрибутов несложно. Алгоритм вычисления приведен ниже. Можно показать, что этот алгоритм корректно вычисляет замыкание X+.
Алгоритм вычисления X+
Input: U - конечное множество атрибутов, множество ФЗ F на U, множество
. Output: X+
- Х0 есть Х.
- Xi+1 есть Xi плюс множество атрибутов А, для которых в F существует ФЗ
.
Условие завершения. Так как U - конечно и
, то существует i, такое, что Xi = Xi+1.
Пример. Вычислим Х+
Пусть
.
- Находим ФЗ, которые в левой части имеют
. Присоединим E и G к X0. X1 = BDEG. Находим ФЗ с левыми частями из
. Находим ФЗ с левыми частями из
.
.

