Кодирование с адаптивным предсказанием
Дифференциальная импульснокодовая модуляция
Самый простой принцип предсказания — это принцип "сохранения предыдущего значения". В этом случае предполагается, что значение предыдущего отсчета сохранится и в последующий момент времени. Так, человек, одеваясь перед выходом из дома, предполагает, что температура на улице сохранится хотя бы на один час. Опровержение этого факта возможно только установлением их разности. Действительно, эксперименты показывают, что разница между предыдущим и последующим значением меньше, чем само значение отсчета. Поэтому для большей части кривой сигнал ошибки может быть не таким значительным.
Приведенная выше формула тогда модифицируется в


Тогда в линию передается разность между текущим и предыдущим значениями:
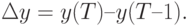
Обратим внимание, что 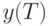 — аппроксимированное значение сигнала. Восстановление сигнала на приеме заключается в том, что к предыдущему значению сигнала прибавляется разность
— аппроксимированное значение сигнала. Восстановление сигнала на приеме заключается в том, что к предыдущему значению сигнала прибавляется разность
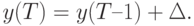
На рис. 10.2 показана одна из реализаций этого метода.
В данном случае предсказатель представляет собой простой регистр, который накапливает значение предыдущего отсчета. В линию передается разностный сигнал.
Для определения следующего разностного отсчета сигнал восстанавливается в сумматоре сложением этого отсчета с предыдущим значением сигнала (см. на рисунке сумм. 2).
Разновидностью этого метода является аппроксимирование на основании нескольких отсчетов. Такой способ позволяет увеличить точность аппроксимации, но требует накопления нескольких отсчетов. При этом последующее значение 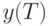 определяется по приведенной выше формуле. При предсказании, основанном на предположении "сохранение предыдущего значения", коэффициенты не меняются, поэтому на приемном конце они те же самые — это позволяет не передавать их по линии, а передать только разность аппроксимированного сигнала.
определяется по приведенной выше формуле. При предсказании, основанном на предположении "сохранение предыдущего значения", коэффициенты не меняются, поэтому на приемном конце они те же самые — это позволяет не передавать их по линии, а передать только разность аппроксимированного сигнала.
Эффективность такого кодирования, как было указано выше, оценивается выигрышем от кодирования и измеряется в отношении мощности сигнала, представленного кодами равномерного квантования, и мощностью сигналов кодирования разностного сигнала.
При ДИКМ такой выигрыш достигает 5 дБ [10.1]. Однако это значение изменяется от характера сигнала. Система с разностным предсказанием становится неэффективной при большом значении разностного сигнала.
Это может произойти из-за возрастания разности соседних отсчетов или из-за нарушения системы предсказания.
Первое увеличивает количество передаваемой информации. Второе является существенным недостатком систем с предсказанием.
Потеря или искажения значения разностных отсчетов приводят к полному искажению восстанавливаемых значений, поскольку ошибка в предыдущем значении сигнала вызывает катастрофические ошибки в определении последующих.
Все это требует передачи на приемный конец величины выигрыша (для контроля качества принимаемого сигнала) и периодического обновления значений коэффициентов (при устойчивом изменении характера сигнала).
Это усложняет реализацию, которая показана на рис. 10.3 (кодер) и 10.4 (декодер).
На этих рисунках показаны кодер и декодер, которые способны передавать три блока информации:
- кодированный разностный сигнал;
- значение выигрыша;
- коэффициенты аппроксимации.
Такая схема позволяет периодически проверять качество разностного кодирования и подстраивать коэффициенты аппроксимации. В этом смысле она адаптируема.
Имеются методы, основанные на вероятностных методах прогнозирования. При этом последовательные n отсчетов рассматриваются как n случайных величин, и определяется вероятность их совместного появления [10.8] — 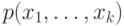 . Прогнозирование всего отсчета основано на определении математического ожидания
. Прогнозирование всего отсчета основано на определении математического ожидания
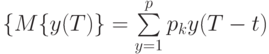
где 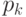 — вероятность появления
— вероятность появления  -го отсчета.
-го отсчета.
При этом в линию передается разность между реальной величиной в момент  и его прогнозируемым значением (математическим ожиданием).
и его прогнозируемым значением (математическим ожиданием).
 .
.
Вероятностные формулы предсказания могут иметь самый различный характер: от формул, предполагающих наличие вероятностного закона, например, распределение вероятности по формуле Пуассона [10.8], до линейнокусочной аппроксимации значений вероятности. Во всех случаях на сторону приема передаются параметры формулы прогнозирования. Моментами передачи, кроме момента инсталляции, могут быть моменты изменения на основе новой статистики (адаптация параметров). Вероятностные методы связаны с нахождением оптимального соотношения сбора отсчетов (чем больше, тем лучше) и своевременной реакцией на изменения (чем больше собранных отсчетов, тем реакция медленнее).
Из всего сказанного можно сделать вывод, что эффективность кодирования с адаптивным предсказанием зависит от сложности адаптивной логики и числа отсчетов для следующего предсказания. Но существует оптимальная точка эффективности предсказания между большим накоплением статистики (осторожная тактика) и быстротой реакции на изменение (тактика быстрого реагирования).
Вычисление коэффициентов предсказания не обязательно проводить в реальном масштабе времени. Их расчет производится на основании математических моделей, исходя из выигрыша от предсказания. Отношение мощности входного сигнала к мощности разностного сигнала называется выигрышем предсказания [10.1].
Поскольку при рассматриваемом методе передачи кодируется разностный сигнал, имеющий меньшую мощность, то такой метод обеспечивает высокий уровень выигрыша предсказания (от 13 до 20 дБ).



