Проблемы алгоритмов архивации с потерями
Первыми для архивации изображений стали применяться привычные алгоритмы. Те, что использовались и используются в системах резервного копирования, при создании дистрибутивов и т.п. Эти алгоритмы архивировали информацию без изменений. Однако основной тенденцией в последнее время стало использование новых классов изображений. Старые алгоритмы перестали удовлетворять требованиям, предъявляемым к архивации. Многие изображения практически не сжимались, хотя "на взгляд" обладали явной избыточностью. Это привело к созданию нового типа алгоритмов - сжимающих с потерей информации. Как правило, степень сжатия и, следовательно, степень потерь качества в них можно задавать. При этом достигается компромисс между размером и качеством изображений.
Одна из серьезных проблем машинной графики заключается в том, что до сих пор не найден адекватный критерий оценки потерь качества изображения. А теряется оно постоянно - при оцифровке, при переводе в ограниченную палитру цветов, при переводе в другую систему цветопредставления для печати, и, что для нас особенно важно, при архивации с потерями. Можно привести пример простого критерия: среднеквадратичное отклонение значений пикселов ( 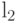 мера, или root mean square - RMS ):
мера, или root mean square - RMS ):

По нему изображение будет сильно испорчено при понижении яркости всего на 5% (глаз этого не заметит - у разных мониторов настройка яркости варьируется гораздо сильнее). В то же время изображения со "снегом" - резким изменением цвета отдельных точек, слабыми полосами или "муаром" будут признаны "почти не изменившимися" (Объясните, почему?). Свои неприятные стороны есть и у других критериев.
Рассмотрим, например, максимальное отклонение:

Эта мера, как можно догадаться, крайне чувствительна к биению отдельных пикселов. Т.е. во всем изображении может существенно измениться только значение одного пиксела (что практически незаметно для глаза), однако согласно этой мере изображение будет сильно испорчено.
Мера, которую сейчас используют на практике, называется мерой отношения сигнала к шуму ( peak-to-peak signal-to-noise ratio - PSNR ).

Данная мера, по сути, аналогична среднеквадратичному отклонению, однако пользоваться ей несколько удобнее за счет логарифмического масштаба шкалы. Ей присущи те же недостатки, что и среднеквадратичному отклонению.
Лучше всего потери качества изображений оценивают наши глаза. Отличной считается архивация, при которой невозможно на глаз различить первоначальное и разархивированное изображения. Хорошей - когда сказать, какое из изображений подвергалось архивации, можно только сравнивая две находящихся рядом картинки. При дальнейшем увеличении степени сжатия, как правило, становятся заметны побочные эффекты, характерные для данного алгоритма. На практике, даже при отличном сохранении качества, в изображение могут быть внесены регулярные специфические изменения. Поэтому алгоритмы архивации с потерями не рекомендуется использовать при сжатии изображений, которые в дальнейшем собираются либо печатать с высоким качеством, либо обрабатывать программами распознавания образов. Неприятные эффекты с такими изображениями, как мы уже говорили, могут возникнуть даже при простом масштабировании изображения.
Алгоритм JPEG
JPEG - один из самых новых и достаточно мощных алгоритмов. Практически он является стандартом де-факто для полноцветных изображений [6.1]. Оперирует алгоритм областями 8х8, на которых яркость и цвет меняются сравнительно плавно. Вследствие этого, при разложении матрицы такой области в двойной ряд по косинусам (см. формулы ниже) значимыми оказываются только первые коэффициенты. Таким образом, сжатие в JPEG осуществляется за счет плавности изменения цветов в изображении.
Алгоритм разработан группой экспертов в области фотографии специально для сжатия 24-битных изображений. JPEG - Joint Photographic Expert Group - подразделение в рамках ISO - Международной организации по стандартизации. Название алгоритма читается ['jei'peg]. В целом алгоритм основан на дискретном косинусоидальном преобразовании (в дальнейшем ДКП), применяемом к матрице изображения для получения некоторой новой матрицы коэффициентов. Для получения исходного изображения применяется обратное преобразование.
ДКП раскладывает изображение по амплитудам некоторых частотных компонент. Таким образом, при преобразовании мы получаем матрицу, в которой многие коэффициенты либо близки, либо равны нулю. Кроме того, благодаря несовершенству человеческого зрения, можно аппроксимировать коэффициенты более грубо без заметной потери качества изображения.
Для этого используется квантование коэффициентов ( quantization ). В самом простом случае - это арифметический побитовый сдвиг вправо. При этом преобразовании теряется часть информации, но может достигаться большая степень сжатия.
