Методы контекстного моделирования
Применение методов контекстного моделирования для сжатия данных опирается на парадигму сжатия с помощью "универсальных моделирования и кодирования" (universal modelling and coding), предложенную Риссаненом (Rissanen) и Лэнгдоном (Langdon) в 1981 году [3.12]. В соответствии с данной идеей процесс сжатия состоит из двух самостоятельных частей:
- моделирование;
- кодирование.
Под моделированием понимается построение модели информационного источника, породившего сжимаемые данные, а под кодированием - отображение обрабатываемых данных в сжатую форму представления на основании результатов моделирования (рис. 3.1). "Кодировщик" создает выходной поток, являющийся компактной формой представления обрабатываемой последовательности, на основании информации, поставляемой ему "моделировщиком".
Схема процесса сжатия данных в соответствии с концепцией универсальных моделирования и кодирования представлена на рис. 3.1

Рис. 3.1. Схема процесса сжатия данных в соответствии с концепцией универсальных моделирования и кодирования
Следует заметить, что понятие "кодирование" часто используют в широком смысле для обозначения всего процесса сжатия, т.е. включая моделирование в данном нами определении. Таким образом, необходимо различать понятия кодирования в широком смысле (весь процесс) и в узком (генерация потока кодов на основании информации модели). Понятие "статистическое кодирование" также используется, зачастую с сомнительной корректностью, для обозначения того или иного уровня кодирования. Во избежание путаницы ряд авторов применяет термин "энтропийное кодирование" для кодирования в узком смысле. Это наименование далеко от совершенства и встречает вполне обоснованную критику. Далее в этой главе процесс кодирования в широком смысле будем именовать "кодированием", а в узком смысле - "статистическим кодированием", или "собственно кодированием".
Из теоремы Шеннона о кодировании источника [3.13] известно, что символ 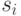 , вероятность появления которого равняется
, вероятность появления которого равняется  , выгоднее всего представлять
, выгоднее всего представлять  битами, при этом средняя длина кодов может быть вычислена по приводившейся ранее формуле (1). Практически всегда истинная структура источника скрыта, поэтому необходимо строить модель источника, которая позволила бы нам в каждой позиции входной последовательности найти оценку
битами, при этом средняя длина кодов может быть вычислена по приводившейся ранее формуле (1). Практически всегда истинная структура источника скрыта, поэтому необходимо строить модель источника, которая позволила бы нам в каждой позиции входной последовательности найти оценку  вероятности появления каждого символа
вероятности появления каждого символа 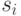 алфавита входной последовательности.
алфавита входной последовательности.
Оценка вероятностей символов при моделировании производится на основании известной статистики и, возможно, априорных предположений, поэтому часто говорят о задаче статистического моделирования. Можно сказать, что моделировщик предсказывает вероятность появления каждого символа в каждой позиции входной строки, отсюда еще одно наименование этого компонента - "предсказатель", или "предиктор" (от "predictor"). На этапе статистического кодирования выполняется замещение символа 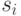 с оценкой вероятности появления
с оценкой вероятности появления  кодом длиной
кодом длиной  битов.
битов.
Рассмотрим пример. Предположим, что мы сжимаем последовательность символов алфавита {'0','1'}, порожденную источником без памяти, и вероятности генерации символов следующие: p('0') = 0.4, p('1') = 0.6. Пусть наша модель дает такие оценки вероятностей: q('0') = 0.35, q('1') = 0.65. Энтропия H источника равна
 .
.
Если подходить формально, то "энтропия" модели получается равной 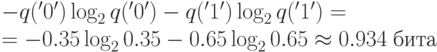 .
.
Казалось бы, что модель обеспечивает лучшее сжатие, чем это позволет формула Шеннона. Но истинные вероятности появления символов не изменились! Если исходить из вероятностей p, то '0' следует кодировать  , а для '1' нужно отводить
, а для '1' нужно отводить  бита. Для оценок вероятностей q мы имеем
бита. Для оценок вероятностей q мы имеем  бита и
бита и  бита соответственно. При каждом кодировании на основании информации модели в случае '0' мы будем терять 1.515 - 1.322 = 0.193 бита, а в случае '1' выигрывать 0.737 - 0.621 = 0.116 бита. С учетом вероятностей появления символов средний проигрыш при каждом кодировании составит 0.4·0.193 - 0.6·0.116 = 0.008 бита.
бита соответственно. При каждом кодировании на основании информации модели в случае '0' мы будем терять 1.515 - 1.322 = 0.193 бита, а в случае '1' выигрывать 0.737 - 0.621 = 0.116 бита. С учетом вероятностей появления символов средний проигрыш при каждом кодировании составит 0.4·0.193 - 0.6·0.116 = 0.008 бита.
Правильность декодирования обеспечивается использованием точно такой же модели, что была применена при кодировании. Следовательно, при моделировании для сжатия данных нельзя пользоваться информацией, которая неизвестна декодеру.
Осознание двойственной природы процесса сжатия позволяет осуществлять декомпозицию задач компрессии данных со сложной структурой и нетривиальными взаимозависимостями, обеспечивать определенную самостоятельность процедур, решающих частные проблемы, сосредотачивать больше внимания на деталях реализации конкретного элемента.
Задача статистического кодирования была в целом успешно решена к началу 1980-х годов. Арифметический кодер позволяет сгенерировать сжатую последовательность, длина которой обычно всего лишь на десятые доли процента превышает теоретическую длину, рассчитанную с помощью формулы (1) (см. пункт "Арифметическое сжатие" главы 1). Более того, применение современной модификации арифметического кодера - интервального кодера - позволяет осуществлять собственно кодирование очень быстро. Скорость статистического кодирования составляет миллионы символов в секунду на современных ПК.
В свете вышесказанного, повышение точности моделей является, фактически, единственным способом существенного улучшения сжатия.
