Решение уравнений
Цель лекции. Показать технику численного решения нелинейных уравнений с использованием сервисов MathCAD. Показать различные методы аналитического решения систем линейных уравнений.
4.1. Численное решение нелинейных уравнений
Относительно небольшое количество задач решения уравнений можно решить аналитически. Аналитическое решение предполагает точное определение корней либо нахождение алгоритма, по которому корни всегда могут быть найдены. На практике часто приходится искать решение при помощи численных методов [1, 11]. Уравнения решаются численными методами с заданной погрешностью. В MathCAD погрешность задается системной константой TOL. Как правило, отыскание корней алгебраического уравнения (или системы уравнений) численными методами связано с двумя задачами:
- локализация корней, т. е. определение их существования в принципе, а также исследование их количества и примерного расположения;
- собственно отыскание корней с заданной погрешностью
Для численного решения уравнений в MathCAD существуют встроенные функции[1, 10], в которых реализованы алгоритмы известных численных методов: итерационный метод секущих; различные градиентные методы и другие. Почти все встроенные функции предполагают, что корни уже приблизительно локализованы.
Использование функции root()
Рассмотрим решение простейших уравнений вида F(x)=0. Решить уравнение – значит найти все его корни, т.е. такие числа, при подстановке которых в исходное уравнение получим верное равенство. Если функция нескольких аргументов F(x, у, ..)=0. , все остальные значения должны быть заданы для искомого x. Для локализации корней (исследования их количества и примерного расположения) полезно построить график функции и определить все точки пересечения графика функции с осью OX.
Функция root () вычисляет значение переменной, при котором F(x, у, ..)=0. Если уравнение имеет несколько корней, функцию надо вызывать соответствующее число раз. Вычисления реализуются итерационным методом. Данный метод заключается в постепенном приближении к искомому корню с некоторой точностью от начального значения переменной. Точность вычислений задаётся системной переменной TOL, определённой в меню Tools/ Worksheet Options.. По умолчанию равной 0.001.
root(F(x, у, ...), x, [a, b]) возвращает с заданной точностью значение переменной, x, лежащей между a и b при котором функция равна нулю. Значения F() для a и b должны быть разных знаков. Третий аргумент не обязателен. Выбор решения определяется выбором начального значения переменной
Пример 4.1
Решить уравнение 
- Зададим функцию

- Найдем начальные значения корней. Для этого построим график функции. Подберем масштаб для наилучшего визуального наблюдения точек пересечения графика с осью OX.
- Точки пересечения графика с осью OX лежат в интервалах (-1; 0) и (0; 1)
- Определили начальные приближения корней. Используем функцию root()
- Можно провести проверку,

1 корень:



Проверка: 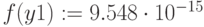
2 корень:
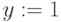


Проверка: 
Если корней уравнения много (больше двух) или надо исследовать определенную область на наличие корней, применяют сканирование. Оно состоит в последовательном поиске корня, начиная из множества пробных точек, покрывающих расчетную область.
Пример 4.2
Решить уравнение  для
для  .
.
Осуществляется решение уравнения при помощи функции root, для нескольких последовательных начальных значений корней. Результат выдается в виде табулированных значений – таблицы.
- Задаем уравнение F1().
- Строим график.
- Всегда существует вероятность "просмотреть" корень, расположенный между узлами сканирования. Начальное значение корня z0 вводим как табулированную переменную в визуальной области корней, определенной по графику.
- Строим функцию U(z0) как решение через root() - значение корня уравнения F1(z0,y)=0. То есть определяется разный корень в зависимости от начального значения z0.
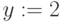
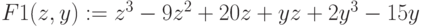
Начальное значение корня z:



Проверка:
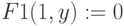


Функция поиска корней полинома polyroots()
Для поиска корней обычного полинома р(х) степени n MathCAD содержит очень удобную функцию:
polyroots(V) возвращает вектор корней многочлена (полинома) степени n, коэффициенты которого находятся в векторе V, имеющем длину равную n+1.
Пример 4.3
Решить уравнение  .
.
Осуществляется решение уравнения при помощи функции polyroots() (Рис.4.3).
- Задаем вектор, элементы которого – коэффициенты полинома, начиная со свободного члена.
- Используем функцию polyroots().
- Решение представляется в виде матрицы, включающей все корни, в том числе и комплексные.

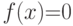


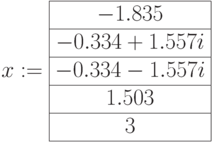
Проверка:



