НОУ ИНТУИТ | MATHCAD 14: Основные сервисы и технологии. Лекция 3: Графика

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Уральский государственный экономический университет

Опубликован: 24.04.2013 | Доступ: свободный | Студентов: 2937 / 1132 | Длительность: 06:24:00

Темы: Математика, Программное обеспечение, Физика, Образование

Специальности: Математик, Физик

Теги: алгебра, анализ, вычисления, теория вероятностей, теория чисел

|

Вам нравится? Нравится 80 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

3 способ. Использование функции CreateMesh() . Встроенная функция в MathCAD для построения графика поверхности. Создает массив, представляющий х-, у- и z-координаты параметрической поверхности, заданной функцией F(). Создает сетку на поверхности определенной функции F() с параметрами , заданными аргументами.

M=CreateMesh (F, x0, x1, y0, y1, xgrid, ygrid, fmap),

F- функция,

x0, x1, y0, y1 – диапазон изменения переменных x и y,

xgrid, ygrid – количество точек переменной х и количество точек переменной y (размеры сетки переменных), количество точек можно задать один раз.

fmap – векторная функция от трех аргументов, задающая преобразование координат, определяет систему координат: декартову, сферическую или цилиндрическую. Если параметр присутствует, то график будет построен в указанной системе координат. Для графика в декартовой системе этот аргумент можно не вводить.

Имеются две встроенные графические функции, которые могут использоваться в аргументах fmap: sph2xyz и syl2xyz.

cyl2xyz – функция преобразования координат из цилиндрической системы в декартову;

ph2xyz – функция преобразования координат из сферической системы в декартову.

На pис.3.26 показано построение графика функции примера с применением CreateMesh() . Указаны границы изменения x – от 8,2 до 10, границы изменения y, – от 10,2 до 12 количество точек сетки – 20 для x и для y. График строится от значений x и y.

$W(x,y):=\ln[(x-8)(y-10)]$

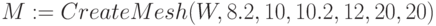
M:=CreateMesh(W,8.2,10,10.2,12,20,20)

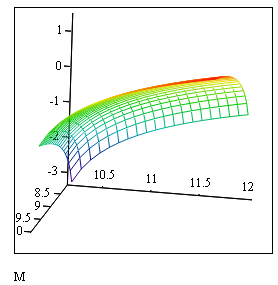
Рис. 3.26. Листинг построения графика поверхности примера 3.10 с использованием функции CreateMesh()

Если не указать параметры сетки, функция CreateMesh по умолчанию создает сетку на поверхности с диапазоном изменения переменных от -5 до 5 и с сеткой 20x20 точек. M=CreateMesh (W) (Рис.3.27).

$W1(x,y):=\ln[(x-8)(y-10)]$

M:=CreateMesh(W1)

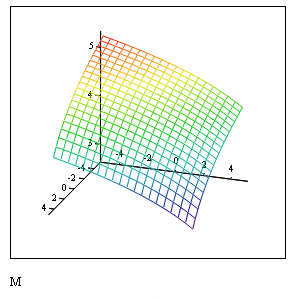
Рис. 3.27. Листинг построения графика поверхности примера 3.10 с использованием функции CreateMesh() (параметры по умолчанию)

Построение поверхности, заданной параметрически

При построении трехмерных поверхностей и объемных фигур можно использовать параметрическое задание описывающих их функций. При этом все три координаты задаются как функции от двух параметров u и v – X(u,v), Y(u,v), Z(u,v). Поверхности задаются значениями координат всех точек. При этом в шаблоне графики указываются три матрицы, хранящие массивы этих координат, X, Y Z.

Сначала необходимо задать векторы значений параметров 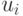и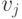
Определить матрицы координат x(u,v), y(u,v) и y(u,v). Ввести как индексные переменные.
Вызвать график поверхности (Graph -> Surface Plot ). В шаблон занести имена матриц. Чтобы получилась фигура вращения, имена вводятся в скобках.
Настроить график.

Пример 3.11

На pис.3.28 показано построение объемной фигуры по точкам. (50 точек). Фигура задана параметрически, параметры – углы $\theta$ и $\varphi$ . Координаты x,y,z вводятся как индексированные переменные, индексы – ранжированные переменные.

N:=50 , i:=0..N , j:=0..N

$\phi(i):=\frac{i \cdot 10}{N}-5$

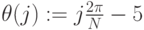
$\theta(j):=j\frac{2\pi}{N}-5$

$X_{i,j}:=\sin{(\phi(i))}(1+0.2\theta(j))$

$Y_{i,j}:=0.2\sin{(\phi(i))}\cos{(\theta(j))}$

$Z_{i,j}:=\cos{(\phi(i))}(1+0.2\theta(j))$

Рис. 3.28. Листинг примера. 3.11. Поверхность задана параметрически

Построение поверхности, заданной в векторной параметрической форме

Поверхность может быть задана в векторной форме. В этом случае функция вводится в виде матрицы, элементы которой – функции параметров, как и сама поверхность. На pис.3.27 показано построение объемной фигуры примера 3.11, заданной в виде матрицы от параметров - углов $\theta$ и $\varphi$ . Количество линий сетки можно изменить в окне форматирования 3-D Plot Format, вкладка QuickPlot Data .

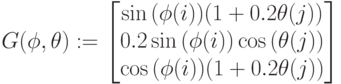
$G(\phi,\theta):=\begin{bmatrix} \sin{(\phi(i))}(1+0.2\theta(j)) \\ 0.2\sin{(\phi(i))}\cos{(\theta(j))} \\ \cos{(\phi(i))}(1+0.2\theta(j)) \end{bmatrix}$

Рис. 3.29. Листинг примера. 3.11. Функция задана в векторной параметрической форме

3.3.2. 3D точечный график

Трехмерный график можно представить в виде пространственной кривой. Пространственные кривые задаются, как правило, параметрически, и параметр является непрерывной действительной величиной. Рассмотрим два способа построения.

Пример 3.12

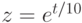Построить пространственную кривую, у которой координаты определены следующим образом: $x=\cos{(3t)}$ , $y=\sin{(3t)}$ , $z=e^{t/10}$ .

1 способ. Кривая в пространстве задается аналогично параметрическому заданию поверхности (пример 3.11).

Задать значения параметра t в виде ранжированной переменной, для t выбирается номер точки (0-100).
Определить координаты x, y, z как индексированные переменные параметра t.
Вызвать командой с панели Графика Graph / 3D Scatter Plot (график 3D точечный), в шаблон занести имена матриц в скобках (Рис.3.28).
Настроить график в окне форматирования.

На графике показаны максимальные минимальные значения

t:=0..100

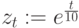
$x_t:=\cos{(3t)}$ , $y_t:=\sin{(3t)}$ , $z_t:=e^{\frac{t}{10}}$

Рис. 3.30. Листинг примера 3.12. Параметрическое задание кривой

2 способ. (Рис.3.31). Векторная форма. Функция задается в виде матрицы-вектора. Для построения графика используется функция CreateSpace()

CreateSpace (R , t0, t1, tgrid, fmap): встроенная функция , создающая массив представляющий х-, у- и z-координаты параметрической пространственной кривой, заданной функцией R() ; и сетку точек на кривой, определенной функцией R() с параметрами , заданными аргументами ,

t0 и t1 – диапазон изменения параметровй, tgrid – размер сетки переменной, fmap – функция отображения аналогично функции CreateMesh() (необязательный параметр). Аргумент t выбирается из указанного интервала: t0=0 t1=10, сетка tgrid=100 точек. Создает сетку точек на кривой.

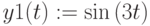$x1(t):=\cos{(3t)}$ , $y1(t):=\sin{(3t)}$ , $z1(t):=e^{\frac{t}{10}}$

$R(t):=\begin{pmatrix} x1(t) \\ y1(t) \\ z1(t) \end{pmatrix}$

M:=CreateMesh(R,0,10,100)

Рис. 3.31. Листинг примера 3.12. Векторное задание кривой. Использование CreateSpace()

Основные итоги

Представлены методы построения графиков функций одной переменной и двух переменных в различных системах координат. На многих примерах показаны различные варианты задания функции, определяющие график: обычным образом (аргументы –скаляры), параметрически, а также в виде матриц и ранжированных переменных. Рассмотрены различные способы построения: автоматическое построение, с построением сетки, с использованием функций CreateMesh() и CreateSpace(). Описаны способы форматирования и настройки графика.

Задания для самостоятельного выполнения

Построить в декартовых координатах на одном шаблоне графики функций: , , , .
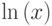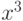- Выбрать пределы изменения x и функции автоматически.
- Изменить пределы: для x и для функций, установить линии сетки, изменить вид кривых (различные линии, маркеры, толщину и т.д.), ввести легенду
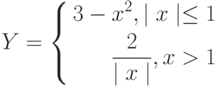
Построить график функции Y. Использовать условную функцию. $Y=\left\{ \begin{aligned} 3-x^2, \mid x \mid\le1\\ \frac{2}{\mid x \mid}, x>1\\ \end{aligned} \right.$
Построить график – область определения функции $Z=\sqrt{(x^2+2x-20)(7x-1)}$ , в области вещественных чисел, где функция не существует, принять z=0
Построить график функции 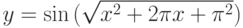$y=\sin{(\sqrt{x^2+2\pi x+\pi^2})}$ для табулированных значений x, [-10;10] с шагом=0.5. Показать значения x y. Показать точки на графике.
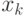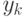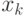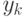Построить график функции $y=\arctan{(\mid x \mid)}$ для 20 точек табулированных значений x, [-10;10] с шагом=1. Аргумент и функцию ввести как индексные переменные и Показать значения и . Показать точки на графике. Ввести линию x=0 в точке особенности как риску.
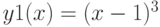Построить графики и вычислить площадь плоской фигуры, ограниченной линиями и : а) , б) ,
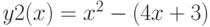
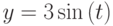Построить графики кривых, заданных параметрически. Оформить. Показать линии сетки. а) $x=5\cos{(t)}$ и $y=3\sin{(t)}$ для t на интервале $[{0;3\frac{\pi}{2}}]$ с шагом =0.01. б) b 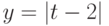для t на интервале [-20;20].
Построить в полярных координатах на одном графике : архимедову спираль 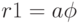$r1=a\phi$ , логарифмическую спираль $r2=ae^{m\phi}$ , кардиоду $r3=10(1+\cos{\phi})$ , (параметры задайте сами). $\varphi$ меняется с шагом 0,1 в пределах: $0 – 6 \pi$
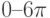
Построить в полярных координатах $r1=\sin{(3\alpha)}$ , $r2=\sin{(5\alpha)}$ , $\alpha$ меняется с шагом 0,01 в пределах: $0 – 2 \pi$ .
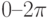Показать область определения функции $R=\sqrt{5\cos{(3\phi)}}}$ . Построить график в полярных координатах. В области вещественных чисел, где функция не существует, принять R=0,5.
Построить график в полярных координатах функции 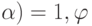$R=a\sec{(3\phi)}$ , $\rho(\phi)=\alpha\sin{(\alpha)}\cos{(\alpha)}$ , $\alpha)=1, \varphi$ меняется от 0 до 8 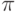$\pi$ с шагом 0.05.
Построить графики поверхности функции: $Y=\frac{a(x-5)}{b(y-2)^3}$ . Параметры a и b введите сами. Показать максимальные и минимальные значения, ввести линии сетки. а) в общем виде, б) с помощью сетки и индексированных переменных, по 30 точкам. Пределы: для x : 0 – 5, для y: 0-1,8. в) с помощью функции CreateMesh()
Построить график . Показать максимальные и минимальные значения.
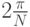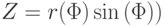Построить фигуру, заданную параметрически, с помощью сетки по 30 точкам , N=30. Параметры – углы $\Phi$ и $\Psi$ . Угол $\Phi$ меняется с шагом $3\frac{\pi}{N}$ , угол $\Psi$ с шагом $2\frac{\pi}{N}$ : $r(\Phi)=4e^{\frac{\Phi}{5}}$ , $R(\Phi)=8e^{\frac{\Phi}{5}}$ . $X=(R(\Phi)+r(\Phi)\cos{(\Psi)}\cos{(\Phi)})$ , $Y=(R(\Phi)+r(\Phi)\cos{(\Psi)}\sin{(\Phi)})$ , $Z=r(\Phi)\sin{(\Phi)})$ . Ввести индексы для углов $\Phi$ и $\Psi$ как ранжированные переменные Ввести углы $\Phi$ и $\Psi$ как индексные переменные Построить матрицы X , Y и Z как двумерные индексные переменные
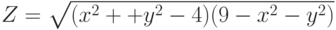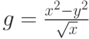Построить область определения функций: $Z=\sqrt{(x^2++y^2-4)(9-x^2-y^2)}$ , $g=\frac{x^2-y^2}{\sqrt{x}}$ .

Ключевые термины

Graph - панель графики.

Formatting Currently Selected X-Y Plot – окно форматирования двумерного графика.

trace - опция форматирования, позволяющая ет точно определить значение функции в любой точки графика.

if(cond, x, y) - условная функция.

параметрическое задание функции - устанавливается зависимость (x,y) точки плоскости от значения параметра t.

полярный график - график функции r(q), заданной в полярных координатах, где полярный радиус r зависит от полярного угла q.

3-D Plot Format - окно форматирования трехмерного графика.

CreateMesh () - встроенная функция в MathCAD, создающая массив, представляющего х-, у- и z-координаты поверхности, заданной функцией F(); и сетку на поверхности определенной функции F() с параметрами , заданными аргументами.

CreateSpace ()- встроенная функция в MathCAD создающая массив представляющий х-, у- и z-координаты параметрической пространственной кривой, заданной функцией R() ; и сетку точек на кривой, определенной функцией R() с параметрами , заданными аргументами .

Surface Plot - опция панели Graph для построения графика поверхности

3D Scatter Plot - опция панели Graph для построения 3-D точечного графика.

Дальше >>

Авторизоваться

MATHCAD 14: Основные сервисы и технологии

Графика