НОУ ИНТУИТ | Классические и квантовые вычисления. Лекция 12: Быстрые квантовые алгоритмы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 611 / 26 | Оценка: 5.00 / 4.50 | Длительность: 19:30:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист

|

Вам нравится? Нравится 10 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В лекции приводится "задача о скрытой подгруппе", дается ее решение, рассмотрен квантовый алгоритм для решения задачи о нахождении периода числа, описан процесс построения измеряющего оператора.

Единственное нетривиальное использование квантовых свойств для вычислений, которое мы уже рассмотрели, — это решение универсальной переборной задачи алгоритмом Гровера, изложенным в "Определение квантового вычисления. Примеры" . К сожалению, при этом достигается лишь полиномиальное ускорение. Поэтому никаких серьезных следствий для теории сложности вычислений (типа $\BQP\supset \BPP$ ) алгоритм Гровера не дает. В настоящее время нет доказательства того, что квантовые вычисления превосходят по скорости классические вероятностные. Но есть косвенные свидетельства в пользу такого утверждения. Первое из них — пример задачи с оракулом (т.е. процедурой типа "черного ящика"), для которой существует полиномиальный квантовый алгоритм, в то время как любой классический вероятностный алгоритм экспоненциален^{1Следует иметь в виду, что сложность задач с оракулом часто отличается от сложности обычных вычислительных задач. Классический пример — теорема о том, что [36, 37]. Оракульный аналог этого утверждения неверен [30]!}. Этот пример, построенный Д. Саймоном [42], называется задачей о скрытой подгруппе в $(\ZZ_2)^k$ . 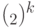В дальнейшем мы решим также задачу о скрытой подгруппе в 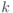$\ZZ^k$ , обобщающую все результаты из этого раздела.

Задача о скрытой подгруппе. Пусть — конечная группа, причем задано некоторое представление элементов двоичными словами. Имеется устройство ( оракул ), вычисляющее функцию $f\colon G\to\cb^n$ со следующим свойством:

$\begin{equation}\label{скр-подгруппа} f(x)=f(y)\,\ \Longleftrightarrow\,\ x-y\in D, \end{equation}$

( 12.1)

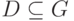где $D\subseteq G$ — некоторая заранее неизвестная подгруппа. Нужно найти эту подгруппу.

Задача о скрытой подгруппе в 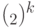$(\ZZ_2)^k$ .

Мы рассмотрим сформулированную выше задачу в случае $G=(\ZZ_2)^k$ . Элементы этой группы

можно представлять строками длины из нулей и единиц; групповая операция — побитовое сложение по модулю 2.

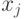Легко доказать, что нельзя быстро найти "скрытую подгруппу" на классической вероятностной машине. (Классическая машина посылает на вход "черного ящика" строки $x_1,\dots,x_l$ и получает ответы $y_1,\dots,y_l$ . Каждый следующий вопрос x_j зависит от предыдущих ответов 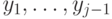$y_1,\dots,y_{j-1}$ и некоторого случайного числа .)

Утверждение 12.1. Пусть $n\ge k$ . Для любого классического вероятностного алгоритма, делающего не более $2^{k/2}$ обращений к оракулу, существует подгруппа $D\subseteq(\ZZ_2)^k$ и соответствующая функция $f\colon (\ZZ_2)^k\to\cb^n$ , для которой алгоритм ошибается с вероятностью $>\slashfrac{1}{3}$ .

Доказательство. Для одной и той же подгруппы существует несколько различных оракулов . Мы будем считать, что один из них выбирается случайно и равновероятно. 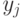(Если алгоритм ошибается с вероятностью $>\slashfrac{1}{3}$ при случайном оракуле, то он также будет ошибаться с вероятностью $>\slashfrac{1}{3}$ при каком-нибудь конкретном оракуле.) Случайный оракул обладает следующим свойством: если очередной ответ y_j не совпадает ни с одним из предыдущих ответов 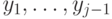$y_1,\dots,y_{j-1}$ , то он равномерно распределен на множестве 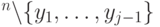$\cb^n\backslash\{y_1,\dots,y_{j-1}\}$ . Таким образом, случайный оракул эквивалентен устройству с памятью, которое на вопрос 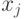x_j выдает наименьшее число $s_j\le j$ , такое что $x_j-x_{s_j}\in D$ . Классическую машину можно изменить таким образом, что она сама будет производить случайный выбор $y_j\double\in\cb^n\backslash\{y_1,\dots,y_{j-1}\}$ , когда s_j=j .

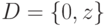Пусть число вопросов к оракулу равно $l\le 2^{k/2}$ . Без уменьшения общности все вопросы различны. В случае $D=\{0\}$ все ответы также различны, то есть s_j=j для всех . Теперь рассмотрим случай $D\double=\{0,z\}$ , где 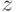выбирается случайно с равномерным распределением на множестве всех ненулевых элементов группы 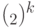$(\ZZ_2)^k$ . Тогда, независимо от используемого алгоритма, s_j=j c вероятностью $\ge 1-\slashfrac{(j-1)}{(2^k-1)}$ . С вероятностью $\ge1-\slashfrac{l(l-1)}{(2(2^k-1))}>\slashfrac{1}{2}$ это имеет место для всех $j=1,\dots,l$ . Напомним, что у нас есть два случайных параметра: 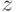и . Мы можем зафиксировать 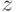таким образом, чтобы вероятность получения ответов s_j=j (для всех ) по-прежнему была больше $\slashfrac{1}{2}$ . Посмотрим, что будет делать классическая машина в этом случае. 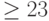Если она выдает ответ " $D=\{0\}$ " с вероятностью $\ge\slashfrac{2}{3}$ , положим $D=\{0,z\}$ — тогда выдаваемый ответ будет неверным с вероятностью $>(\slashfrac{2}{3})\cdot(\slashfrac{1}{2})=\slashfrac{1}{3}$ . Если же вероятность ответа " $D=\{0\}$ " меньше $\slashfrac{2}{3}$ , положим $D=\{0\}$ .

Теперь определим квантовый аналог описанного выше устройства. Соответствующий квантовый оракул — это унитарный оператор

$\begin{equation}\label{кв-оракул} U\colon \ket{x,y}\,\mapsto\,\ket{x,\,y\oplus f(x)}. \end{equation}$

( 12.2)

( $\oplus$ обозначает побитовое сложение). Заметим, что квантовый оракул допускает линейные комбинации разных вопросов, поэтому его можно использовать более эффективно, чем классический оракул.

Пусть Е=G/D , а E^* — группа характеров на , т.е. гомоморфизмов $E\to U(1)$ . В случае $G=(\ZZ_2)^k$ группу E^* можно охарактеризовать следующим образом:

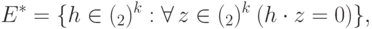
$E^*= \{h \in(\ZZ_2)^k: \forall\, z\in(\ZZ_2)^k\: (h\cdot z=0) \},$

где $h\cdot z$ обозначает скалярное произведение по модулю 2. (Соответствующий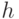

характер имеет вид $z\mapsto(-1)^{h\cdot z}$ .) Покажем, как можно породить случайный элемент $h\in E^*$ , используя оператор

. Породив достаточно много случайных элементов, мы найдем группу E^*

, и, тем самым, исходную подгруппу D.

Начнем с того, что приготовим состояние $\ket{\xi}=2^{-k/2}\sum_{x\in G}\ket{x}=H^{\otimes k}\ket{0^k}$ в одном квантовом регистре. Во второй регистр поместим состояние $\ket{0^n}$ и применим оператор . Затем выбросим второй регистр, т.е. не будем его больше использовать. Получится смешанное состояние

$\rho \,=\, \Tr_2\Bigl(U(\ket{\xi}\bra{\xi}\otimes\ket{0^n}\bra{0^n})U^\dagger \Bigr)\,=\, 2^{-k}\,\sum_{x,y:x-y\in D}\ket{x}\bra{y}.$

Теперь применим оператор $H^{\otimes k}$ :

$\gamma \,=\, H^{\otimes k}\rho H^{\otimes k} \,=\, 2^{-2k} \sum_{a,b}\sum_{x,y:x-y\in D} (-1)^{a\cdot x-b\cdot y}\ket{a}\bra{b}.$

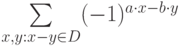Легко видеть, что величина $\sum\limits_{x,y:x-y\in D}(-1)^{a\cdot x-b\cdot y}$ отлична от нуля только в том случае, когда $a=b\in E^*$ . Таким образом,

$\gamma = \frac{1}{|E^*|} \sum_{a\in Е^*} \ket{a}\bra{a}.$

Это в точности матрица плотности для случайного равномерно распределенного элемента группы E^*

. Теперь осталось воспользоваться следующей леммой, которую мы сформулируем в виде задачи.

Задача 12.1. Пусть 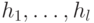$h_1,\dots,h_l$ — независимые случайные равномерно распределенные элементы абелевой группы . Докажите, что они порождают всю группу c вероятностью $\ge 1-\slashfrac{|X|}{2^l}$ .

Таким образом, достаточно случайных элементов, чтобы породить всю группу E^* с вероятностью ошибки $\le 2^{-k}$ . (Такая маленькая вероятность ошибки получается без особых затрат по сравнению с $\slashfrac{1}{3}$ . Чтобы сделать ее еще меньше, эффективнее всего воспользоваться стандартной процедурой: повторить все вычисление несколько раз и выбрать наиболее часто встречающийся ответ).

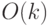Подведем итог: для нахождения "скрытой подгруппы" требуется O(k) обращений к квантовому оракулу. В целом алгоритм имеет сложность O(k^3) .

Дальше >>

Авторизоваться

Классические и квантовые вычисления

Быстрые квантовые алгоритмы

Вопросы и ответы