Класс NP: сводимость и полнота
NP — класс предикатов, вычислимых за полиномиальное время недетерминированными машинами Тьюринга.
Термин "недетерминированный" неудачный, но он уже стал стандартным.
Класс NP определен только для предикатов. Говорят, например, что "свойство графа "иметь гамильтонов цикл1Гамильтонов цикл — замкнутый путь в графе, проходящий через все вершины графа ровно по одному разу. Граф, в котором есть хотя бы один гамильтонов цикл, называется гамильтоновым. " принадлежит NP".
Мы дадим несколько определений этого класса. Первое использует понятие недетерминированной машины Тьюринга. Устройство недетерминированной машины (НМТ) такое же, как и обычной (детерминированной), за одним исключением. У управляющего устройства НМТ есть особые недетерминированные состояния. Находясь в таком состоянии, НМТ может выполнить одно из нескольких действий. Поэтому у НМТ вместо функции переходов есть таблица, в которой для каждой пары (состояние управляющего устройства, текущий символ на ленте) вместо единственно возможного варианта действий (изменение состояния управляющего устройства, запись символа на ленту, сдвиг головки) указан набор возможных действий. Обычные, детерминированные, состояния становятся частным случаем, когда такой набор состоит ровно из одного варианта действий.
Путь вычисления НМТ определяется выбором одного из возможных переходов на каждом такте работы. Недетерминированность приводит к тому, что путей вычисления для НМТ, работающей на данном входном слове, оказывается много.
Определение 2.1. Предикат  принадлежит классу
принадлежит классу  , если существуют НМТ
, если существуют НМТ  и полином
и полином 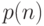 такие, что
такие, что
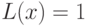
 существует путь вычисления, дающий ответ "да" за время, не превосходящее
существует путь вычисления, дающий ответ "да" за время, не превосходящее  ;
;
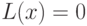
 (1 вариант определения ) нет указанного выше пути; (2 вариант определения ) на любом пути вычисления ответа "да" не получается.
(1 вариант определения ) нет указанного выше пути; (2 вариант определения ) на любом пути вычисления ответа "да" не получается.
Замечание 2.1. Приведенные варианты определения эквивалентны. Чтобы исключить возможность ответов "да" на длинных путях вычисления, достаточно взять НМТ, имитирующую исходную НМТ и подсчитывающую количество сделанных исходной НМТ шагов. Когда число шагов превышает  , машина останавливается.
, машина останавливается.
Замечание 2.2. В предыдущем рассуждении допущена одна тонкая ошибка. В определении ничего не сказано о полиноме 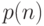 , кроме факта его существования. Если коэффициенты полинома невычислимы, могут возникнуть проблемы с указанным выше способом сведения одного определения к другому (нужно вычислить значение полинома). Чтобы в дальнейшем избегать этой сложности, будем считать, что полином имеет целые коэффициенты.
, кроме факта его существования. Если коэффициенты полинома невычислимы, могут возникнуть проблемы с указанным выше способом сведения одного определения к другому (нужно вычислить значение полинома). Чтобы в дальнейшем избегать этой сложности, будем считать, что полином имеет целые коэффициенты.
Замечание 2.3. Непосредственно из определения 2.1 следует, что  . Является ли это включение строгим? Довольно интенсивные, хотя и безуспешные, попытки ответить на этот вопрос продолжаются уже почти 30 лет. Недавно С.Смейл включил проблему
. Является ли это включение строгим? Довольно интенсивные, хотя и безуспешные, попытки ответить на этот вопрос продолжаются уже почти 30 лет. Недавно С.Смейл включил проблему 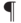 в число трех важнейших математических проблем следующего столетия (две другие — гипотеза Римана и гипотеза Пуанкаре).
в число трех важнейших математических проблем следующего столетия (две другие — гипотеза Римана и гипотеза Пуанкаре).
Второе определение класса NP представляется более естественным. Оно использует понятие полиномиально вычислимого предиката от двух переменных. Определение такого предиката получается комбинацией определений 1.2 и 1.3. Под размером входа для предиката  можно понимать также или
можно понимать также или  , или
, или  — получатся эквивалентные определения.
— получатся эквивалентные определения.
Определение 2.2. Предикат  принадлежит классу NP, если он представим в форме
принадлежит классу NP, если он представим в форме  , где
, где  — полином, а
— полином, а 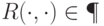 .
.
Пример 2.1. Пусть 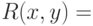 "
"  есть гамильтонов цикл в графе
есть гамильтонов цикл в графе  ". Более точно нужно сказать так: "
". Более точно нужно сказать так: "  есть двоичный код некоторого графа, а
есть двоичный код некоторого графа, а  — код гамильтонова цикла в этом графе (используем такое кодирование, при котором код цикла не длиннее кода графа), такие что
— код гамильтонова цикла в этом графе (используем такое кодирование, при котором код цикла не длиннее кода графа), такие что  ". Возьмем
". Возьмем  . Тогда
. Тогда  будет в точности означать, что в графе найдется гамильтонов цикл.
будет в точности означать, что в графе найдется гамильтонов цикл.
Теорема 2.1. Определения 2.1 и 2.2 эквивалентны.
Опр. 2.1  опр. 2.2. Пусть есть НМТ
опр. 2.2. Пусть есть НМТ  и полином
и полином 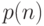 из первого определения. Рассмотрим предикат
из первого определения. Рассмотрим предикат 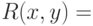 "
"  есть протокол работы
есть протокол работы  на возможном пути вычисления со входом
на возможном пути вычисления со входом  дающего ответ "да" за время, не превосходящее
дающего ответ "да" за время, не превосходящее  ." Длина такого протокола при разумном кодировании линейно зависит от времени вычисления (если использовать в качестве протокола описанную в доказательстве теоремы 1.2 таблицу вычисления, то квадратично), поэтому в качестве
." Длина такого протокола при разумном кодировании линейно зависит от времени вычисления (если использовать в качестве протокола описанную в доказательстве теоремы 1.2 таблицу вычисления, то квадратично), поэтому в качестве  для второго определения можно взять
для второго определения можно взять 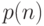 (
(  ), умноженный на подходящую константу.
), умноженный на подходящую константу.
Чтобы закончить доказательство в этом случае, осталось проверить, что 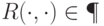 . Это почти очевидно. Мы должны проверить протокол некоторой НМТ, работающей за полиномиальное время. Это займет нас примерно на то же время (совершенно незачем смотреть на одну ячейку экспоненциально долго).
. Это почти очевидно. Мы должны проверить протокол некоторой НМТ, работающей за полиномиальное время. Это займет нас примерно на то же время (совершенно незачем смотреть на одну ячейку экспоненциально долго).
Опр. 2.2  опр. 2.1. Пусть есть
опр. 2.1. Пусть есть  из определения 2.2. Построим
из определения 2.2. Построим  для определения 2.1. Она работает в два этапа.
для определения 2.1. Она работает в два этапа.
Вначале  недетерминированно пишет
недетерминированно пишет  (который в силу определения 2.2 существует для любого слова
(который в силу определения 2.2 существует для любого слова  , для которого
, для которого 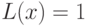 ). Говорят еще, что
). Говорят еще, что  "отгадывает" ("guesses")
"отгадывает" ("guesses")  . Более точно это означает, что
. Более точно это означает, что  находит правый конец входного слова, сдвигается еще на одну ячейку вправо, записывает в нее
находит правый конец входного слова, сдвигается еще на одну ячейку вправо, записывает в нее  , еще раз сдвигается вправо и переходит в такое недетерминированное состояние, в котором она пишет один из символов на ленту, сдвигается вправо и выбирает между сохранением этого состояния и переходом в (уже детерминированное) состояние начала следующего этапа.
, еще раз сдвигается вправо и переходит в такое недетерминированное состояние, в котором она пишет один из символов на ленту, сдвигается вправо и выбирает между сохранением этого состояния и переходом в (уже детерминированное) состояние начала следующего этапа.
После завершения первого этапа на ленте, помимо входного слова  , записано еще и слово
, записано еще и слово  . Теперь
. Теперь  осталось вычислить значение предиката
осталось вычислить значение предиката  за полиномиальное время. Это можно сделать, используя детерминированный алгоритм, существующий в силу определения 2.2.
за полиномиальное время. Это можно сделать, используя детерминированный алгоритм, существующий в силу определения 2.2.
Еще одно определение класса NP есть не более чем вариант определения 2.2, но именно в такой форме его удобно обобщать и получать определения других сложностных классов.
Определение 2.3. Имеются два персонажа: король A rthur (Артур), умственные способности которого полиномиально ограничены, и волшебник M erlin (Мерлин), который интеллектуально всемогущ и знает правильные ответы на все вопросы. Король A интересуется некоторым свойством  (например, "есть ли у графа гамильтонов цикл"), а волшебник M хочет, чтобы король признал наличие этого свойства (ну, скажем, граф стремится к званию гамильтонова и дал M взятку). A не доверяет своему волшебнику, зная его корыстолюбие, и хочет иметь возможность самостоятельно проверить предложенный M ответ.
(например, "есть ли у графа гамильтонов цикл"), а волшебник M хочет, чтобы король признал наличие этого свойства (ну, скажем, граф стремится к званию гамильтонова и дал M взятку). A не доверяет своему волшебнику, зная его корыстолюбие, и хочет иметь возможность самостоятельно проверить предложенный M ответ.
Поэтому они действуют следующим образом. A и M оба смотрят на слово  , после чего M сообщает некоторую информацию (слово
, после чего M сообщает некоторую информацию (слово  ), которая должна убедить A, что
), которая должна убедить A, что 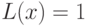 . Используя эту информацию, A проверяет убедительность аргументов M некоторым полиномиальным способом.
. Используя эту информацию, A проверяет убедительность аргументов M некоторым полиномиальным способом.
В этих терминах определение класса NP можно сформулировать так: свойство  принадлежит классу NP, если у Артура есть полиномиальный способ проверять убедительность доводов Мерлина, причем:
принадлежит классу NP, если у Артура есть полиномиальный способ проверять убедительность доводов Мерлина, причем:
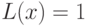
 у M есть способ убедить A в этом;
у M есть способ убедить A в этом;
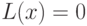
 как бы M ни изощрялся, A не поверит, что
как бы M ни изощрялся, A не поверит, что 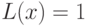 .
.
Эквивалентность этого определения определению 2.2 не вызывает сомнений. Действительно, из-за полиномиальной ограниченности короля A, сообщение волшебника M должно иметь полиномиальный размер. В остальном различия между определениями чисто внешние.
