Проектирование цикла при помощи инварианта

Расширение области значения переменной

Данный метод в значительной мере подобен разобранному в предыдущей секции — если необходимая переменная уже содержится в постусловии, то ее можно использовать для построения инварианта, просто разрешив ей меняться в более широких пределах.

В качестве примера разберем классическую задачу "Жулик на пособии". В оригинальном варианте рассматриваются три потенциально бесконечных упорядоченных по алфавиту списка фамилий — сотрудники исследовательского центра IBM, студенты Колумбийского университета и безработные Нью-Йорка. Требуется найти первую из фамилий, встречающуюся во всех трех списках (в предположении, что она есть).

Задача 8.5. Найдите минимальное число, содержащееся в каждом из трех упорядоченных по возрастанию массивов целых чисел, в предположении, что таковое существует.

Решение Пусть имеющиеся массивы — это , и . Переменные, содержащие значения индексов для каждого из этих массивов, обозначим через , и соответственно, а индексы искомого числа в каждом из них — , и .

Если не включать в предусловие информацию о том, что массивы являются упорядоченными (не забывая об этом, конечно), то пред- и постусловия искомой программы буду иметь вид , и .

Расширение области значений переменных , и — естественный способ построения инварианта в данном случае: . В качестве ограничивающей функции можно взять , выбор начальных присваиваний S0 проблем тоже не вызывает — ясно, что операторы "i=0; j=0; k=0;" сделают инвариант истинным.

В качестве действий, которые будут приближать цикл к завершению можно использовать операторы "i++;", "j++;" и "k++;". При этом понятно, что каждый из них обязан присутствовать в итоговой программе.

Вычислим . Это означает, что увеличение индекса в цикле нужно делать, когда . К сожалению, записать подобное условие в программе невозможно, так как переменной в ней просто может не быть!

Легко заметить, однако, что выполнение условия при истинном инварианте означает, что число меньше искомого в задаче, а это может быть только при условии истинности дизъюнкции . Аналогично заключаем, что если истинна дизъюнкция , то можно увеличивать значение индекса , а при истинности предиката — индекса .

Это уже позволяет написать программу, но если внимательно исследовать доказательство ее правильности, то можно обнаружить возможность для ее упрощения, что и реализовано ниже.

Текст программы

public class Arr3 {
    public static void main(String[] args){    
        int a[] = { 1, 2, 4, 8,16,32,64,128};
        int b[] = {10,12,14,16,18,20,22, 24};
        int c[] = { 9,12,13,16,17,20,21, 24};
        int i = 0, j = 0, k = 0;
        while (true) { 
            if (a[i] < b[j]) {
                i++; continue;
            }
            if (b[j] < c[k]) {
                j++; continue;
            }
            if (c[k] < a[i]) {
                k++; continue;
            }
            Xterm.println("Минимальное общее число=" + a[i]);
            return;
        }
    }
}

Обязательно проверьте все пять условий правильности этой итоговой программы.

Задачи для самостоятельного решения

При решении задач необходимо построить и доказать правильность построенной программы вида "S0;while(e)S;", а при отсутствии в условии задачи явно заданных инварианта цикла и ограничивающей функции объяснить предварительно, каким образом они были получены.

Задача 8.6. Напишите программу, печатающую -ое число Фибоначчи ( , , ). При написании программы используйте , , 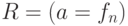, . Число в программе изменять нельзя.

Задача 8.7. Напишите программу, находящую частное и остаток от деления на , не использующую операций умножения и деления. При написании программы положите , , , 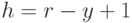. Величины и в программе изменять не разрешается.

Задача 8.8. Напишите программу, находящую наибольший общий делитель двух целых положительных чисел и , не использующую операций умножения и деления и не изменяющую величин и . При написании программы положите , , , .

Указание Воспользуйтесь следующими свойствами наибольшего общего делителя двух чисел не равных одновременно нулю (не забудьте научиться доказывать все эти свойства):

Задача 8.9. Напишите программу, находящую приближенное значение квадратного корня из заданного неотрицательного целого числа . Вот более точная формулировка пред- и постусловия: , . При написании программы величину изменять нельзя. Для построения инварианта удалите из постусловия конъюнктивный член . Оцените временную сложность получившейся программы и сравните ее со сложностью программы, построенной в задаче 8.1.

Задача 8.10. Напишите программу, определяющую первое вхождение заданного целого числа в заданный массив массивов целых чисел ( ). Значения элементов массива и числа , и в программе изменять нельзя. В момент завершения должно быть либо , либо, если числа в массиве нет, . Точные пред- и постусловия требуемой программы таковы: , .

Указание Используйте инвариант, утверждающий, что не находится в уже проверенных строках и среди уже проверенных элементов текущей строки . В качестве ограничивающей функции возьмите .

Задача 8.11. Напишите программу (бинарный или двоичный поиск), определяющую для упорядоченного по неубыванию массива целых чисел и заданного целого числа позицию , в которую может быть вставлено это число без нарушения упорядоченности массива. Точные пред- и постусловия требуемой программы, временная сложность которой не должна превосходить , таковы: , . При написании программы величины , и элементы массива изменять не разрешается, для построения инварианта используйте метод замены константы переменной.

Задача 8.12. Напишите программу, печатающую факториал введенного неотрицательного целого числа, изменять которое нельзя. Для построения инварианта используйте метод замены константы переменной.