НОУ ИНТУИТ | Основы информатики и программирования. Лекция 7: Базисные схемы обработки информации

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный индустриальный университет

Опубликован: 27.09.2006 | Доступ: свободный | Студентов: 3333 / 380 | Оценка: 4.17 / 3.79 | Длительность: 24:17:00

Темы: Программирование, Образование

Специальности: Программист

|

Вам нравится? Нравится 44 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Функции на пространстве последовательностей

Еще одной ситуацией, в которой общая схема итерации значительно упрощается, является задача вычисления индуктивных функций. Такие функции определены на последовательностях X^* элементов из некоторого алфавита . Напомним важнейшие из определений "Высказывания и предикаты" .

Алфавит — произвольное непустое множество.

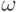Символом алфавита называют любой его элемент, а цепочкой над алфавитом — произвольную последовательность символов $\omega$ . Цепочки часто называют также словами, фразами и предложениями. Пустая цепочка обозначается специальным символом $\varepsilon$ , а множество всех цепочек над алфавитом принято обозначать X^* .

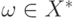Длиной $|\omega|$ цепочки $\omega \in X^*$ называется количество входящих в нее символов. Множество всех цепочек длины не менее обозначают через X^*_k . Справедлива следующая последовательность включений: $X^* \supset X^*_1 \supset X^*_2 \supset X^*_3 \supset \ldots$

Операция $\circ\colon X^*\times X^* \rightarrow X^*$ конкатенации (или сцепления ) двух цепочек определена следующем образом. Пусть $\omega_1 = a_1 a_2 \ldots a_n$ , $\omega_2 = b_1 b_2 \ldots b_m$ , тогда $\omega_1 \circ w_2 = a_1 a_2 \ldots a_n b_1 b_2 \ldots b_m$ .

Теперь можно дать определение индуктивной функции.

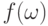Определение 7.4. Функция $f\colon X^* \rightarrow Y$ называется индуктивной, если $f(\omega\circ x)$ можно вычислить, зная $f(\omega)$ и , т.е. если $\exists G\colon Y \times X\rightarrow Y$ такое, что $\forall \omega\in X^* \ \forall x\in X\ f(\omega\circ x) = G(f(\omega),x)$ .

Одним из простейших примеров индуктивной функции является функция длина цепочки $|\omega|\colon X^* \rightarrow \mathbb{Z^+}$ . Она индуктивна, так как для нее существует функция $G\colon \mathbb{Z^+\times X \rightarrow \mathbb{Z^+}$ , определенная формулой G(y,x) = y+1 , удовлетворяющая предыдущему определению.

Для вычисления значения 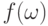$f(\omega)$ индуктивной функции на цепочке $\omega=a_1a_2\ldots a_n$ применяется следующая схема.

Схема вычисления индуктивной функции.

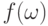Рассматривается последовательность цепочек $\varepsilon$ , a_1 , a_1a_2 , $\ldots$ , $a_1a_2\ldots a_n=\omega$ . Сначала вычисляется значение $f(\varepsilon)$ функции на пустой цепочке $\varepsilon$ , а затем используется отображение , позволяющее найти значение функции на удлиненной цепочке, что дает возможность последовательно определить все требуемые величины вплоть до $f(\omega)$ .

На рис. 7.5 приведена графическая иллюстрация схемы вычисления индуктивной функции.

Рис. 7.5. Схема вычисления индуктивной функции

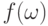Схема вычисления индуктивной функции напоминает метод доказательства по индукции. Аналогом базы индукции является вычисление $f(\varepsilon)$ , а индуктивному переходу соответствует вычисление функции $f(\omega\circ x)$ на удлиненной цепочке $\omega \circ x$ с использованием вычисленного на предыдущем шаге значения $f(\omega)$ .

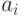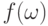Схема вычисления индуктивной функции позволяет легко построить программу вида "S0;while(e)S;", получающую на каждой следующей итерации цикла очередной элемент a_i цепочки (последовательности) $\omega=a_1a_2\ldots a_n$ , которая находит значение $f(\omega)$ . Инвариантом данного цикла является $I=(0\leqslant i \leqslant n\land f=f(a_1a_2\ldots a_i))$ , условием продолжения — $e=(i \leqslant n)$ , S0 должно вычислять $f(\varepsilon)$ , а S — быть программной реализацией функции .

Простым и полезным примером, иллюстрирующим схему вычисления индуктивной функции, является задача нахождения значения многочлена, заданного последовательностью его коэффициентов.

Задача 7.6. Напишите программу, определяющую значение в целой точке многочлена, заданного последовательностью его целых коэффициентов (в порядке убывания степеней).

Заметим, что

$P_n(t)=a_0t^n+a_1t^{n-1}+\ldots+a_{n-1}t+a_n = t\cdot P_{n-1}(t) + a_n$

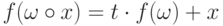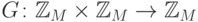, где $P_{n-1}(t)=a_0t^{n-1}+a_1t^{n-2}+\ldots+a_{n-1}$ . Поэтому функция $f\colon (\mathbb{Z}_M)^* \rightarrow \mathbb{Z}_M$ , определенная, как $f(\omega) = f(a_0a_1\ldots a_n) = P_n(t)$ , удовлетворяет соотношению $f(\omega\circ x) = t\cdot f(\omega) + x$ , что доказывает ее индуктивность. Отображение $G\colon\mathbb{Z}_M\times \mathbb{Z}_M\rightarrow\mathbb{Z}_M$ действует по формуле G(y,x) = ty+x

, а $f(\varepsilon)=0$ , что приводит к следующей программе.

Текст программы

public class Pol {
    public static void main(String[] args) throws Exception {
        int t = Xterm.inputInt("t -> ");
        int y = 0;
        try {
            while (true) {
                int x = Xterm.inputInt("x -> ");
                y = t*y + x;
            }
        } catch (Exception e) {
            Xterm.println("\ny = " + y);
        }	    
    }
}

Этот эффективный метод вычисления значения многочлена в точке носит имя схемы Горнера.

Методы доказательства правильности программ, построенных с помощью схемы вычисления индуктивных функций, и обобщение этой схемы, позволяющее применять аналогичный подход для функций, не являющихся индуктивными, будут рассмотрены ниже в "Индуктивные функции на пространстве последовательностей" .

Дальше >>

Авторизоваться

Основы информатики и программирования

Базисные схемы обработки информации

Функции на пространстве последовательностей

Вопросы и ответы