НОУ ИНТУИТ | Основы информатики и программирования. Лекция 6: Спецификация программ и преобразователь предикатов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный индустриальный университет

Опубликован: 27.09.2006 | Доступ: свободный | Студентов: 3332 / 380 | Оценка: 4.17 / 3.79 | Длительность: 24:17:00

Темы: Программирование, Образование

Специальности: Программист

|

Вам нравится? Нравится 44 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Определение простейших операторов языка Java

До сих пор все наши манипуляции с основывались на том, что мы считали известным, как именно выполняются те или иные команды, из которых состоит программа .

Сейчас мы полностью изменим точку зрения. Будем считать первичным предикат и условия, которым он удовлетворяет. Это позволит нам определить в терминах все команды языка, а затем доказывать всевозможные утверждения о программах.

Первым оператором, который мы определим, будет пустой оператор.

Определение 6.6. wp(";", R) = R .

Определение не требует доказательства, однако полезно убедиться, что оно не противоречит нашему внутреннему пониманию того, как именно работает пустой оператор. Проверьте это сами.

Определение 6.7. 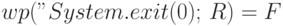wp("System.exit(0);", R) = F .

Выполнение вызова метода " System.exit(0) " приводит к немедленному завершению выполнения программы. Поэтому вполне естественно, что ни при каком начальном состоянии после его выполнения предикат истинным не будет.

Следующее определение связано с последовательным выполнением двух операторов одного за другим.

Определение 6.8. wp("S1; S2;", R) = wp("S1;", wp("S2;", R)) .

В случае последовательного выполнения нескольких операторов данным определением нужно воспользоваться многократно.

Более сложным и интересным является определение оператора присваивания, которое будет рассмотрено нами в двух вариантах. Сначала рассмотрим случай присваивания простой переменной.

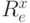Определение 6.9. $wp("x = e;", R) = domain(e) \lands R^x_e$ , где — предикат, описывающий множество всех состояний, в которых может быть вычислено значение (т.е., где определено), а R^x_e обозначает подстановку в предикат выражения вместо всех свободных вхождений переменной .

Это определение может вызвать определенные вопросы, так как на первый взгляд кажется, что оно не соответствует нашему интуитивному пониманию того, что делает оператор присваивания. Поэтому рассмотрим ряд примеров, которые развеют эти сомнения.

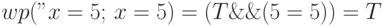$wp("x = 5;", x=5) = (T \&\& (5=5)) = T$ , что вполне правильно, так как присваивание переменной числа 5 всегда делает x=5 .

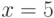$wp("x = 5;", x\ne 5) = (T \&\& (5\ne5)) = F$ , что тоже правильно, ибо присваивание переменной числа 5 никогда не может сделать $x\ne5$ .

Часто можно позволить себе опустить предикат domain(e) и считать, что wp("x = e;", R) = R^x_e , так как присваивание всегда должно выполняться только в тех ситуациях, когда может быть вычислено. В случае сомнений, однако, лучше воспользоваться исходным определением.

$wp("x = 1/y;", x\leqslant0) = (y\ne0)\&\&(1/y\leqslant0) = (y<0)$ .

Случай присваивания элементу массива несколько сложнее, так как выражение b[i] само по себе может оказаться неопределенным из-за некорректного значения индекса . Введем предикат inrange(b,i) , который будет определять множество допустимых значений индекса.

Определение 6.10. Для присваивания элементу массива слабейшее предусловие $wp("b[i] = e;", R) = inrange(b,i) \lands domain(e) \lands R^{b[i]}_e$ .

В качестве примера рассмотрим массив b[0..9] и вычислим слабейшее предусловие $wp("b[i] = i;", b[i] = i) = (inrange(b,i) \lands domain(i) \lands i = i) = ((0 \leqslant i < 10) \lands T \lands T) = (0 \leqslant i < 10)$

Оператор if и слабейшее предусловие

Перед тем, как дать формальное определение оператора if-else в терминах , заметим, что управляющая конструкция if (без else части) эквивалентна использованию пустого оператора в else -ветви. Оператор switch также может быть заменен несколькими вложенными друг в друга операторами if-else. Таким образом, для того чтобы задать все основные конструкции выбора языка Java, достаточно дать определение только одной из них, — конструкции "if (e) S1; else S2;".

Определение 6.11.

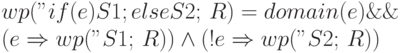
$wp("if (e) S1; else S2;", R) = domain(e)\lands\\ (e \Rightarrow wp("S1;",R))\land (!e \Rightarrow wp("S2;",R))$

В качестве примера использования этого определения убедимся в том, что

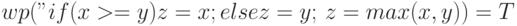
wp("if (x >= y) z=x; else z=y;", z = max(x, y)) = T

В самом деле,

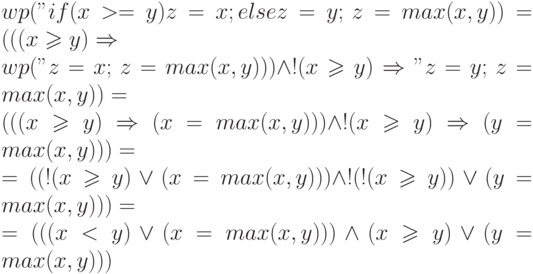
$wp("if (x >= y) z=x; else z=y;", z = max(x, y)) = (((x \geqslant y) \Rightarrow \\ wp("z=x;", z = max(x, y))) \land !(x \geqslant y) \Rightarrow "z=y;", z = max(x, y)) =\\(((x \geqslant y) \Rightarrow (x = max(x, y))) \land !(x \geqslant y) \Rightarrow (y = max(x, y))) =\\ =((!(x \geqslant y) \lor (x = max(x, y))) \land !(!(x \geqslant y)) \lor (y = max(x, y))) =\\ =(((x < y) \lor (x = max(x, y))) \land (x \geqslant y) \lor (y = max(x, y)))$

Покажем, что каждый из двух членов получившейся конъюнкции является тавтологией. Рассмотрим, например, первый из них — 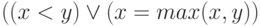$((x < y) \lor (x = max(x, y))$ . Если x<y , то истинен первый член дизъюнкции. В противном случае $x\geqslant y$ и поэтому истинен ее второй член, что и доказывает требуемое. Аналогичные рассуждения можно провести и для выражения $(x \geqslant y) \lor (y = max(x, y)))$ , что и завершает доказательство.

Для практических приложений часто необходимо не вычисление слабейшего предусловия, а лишь проверка того факта, что некоторое другое известное предусловие обеспечивает его выполнение. По этой причине полезна следующая теорема.

Теорема 6.1.

Пусть предикат удовлетворяет условию

$((Q\land e)\Rightarrow wp(S1, R))\land ((Q\land !e)\Rightarrow wp(S2, R)).$

Тогда (и только тогда)

$Q\Rightarrow wp("if (e) S1; else S2;", R).$

Доказательство

$((Q\land e)\Rightarrow wp(S1, R)) = (!(Q\land e)\lor wp(S1, R)) = (!Q\lor !e\lor wp(S1, R)) =\\= (!Q\lor (e\Rightarrow wp(S1, R))) = (Q\Rightarrow (e\Rightarrow wp(S1, R)))$

Аналогично получаем

$((Q\land !e)\Rightarrow wp(S2, R)) = (Q\Rightarrow (!e\Rightarrow wp(S2, R))),$

и, следовательно,

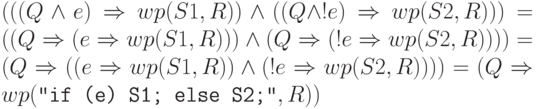
$(((Q\land e)\Rightarrow wp(S1, R))\land ((Q \land !e)\Rightarrow wp(S2, R))) = ((Q\Rightarrow (e\Rightarrow wp(S1, R)))\land (Q\Rightarrow (!e\Rightarrow wp(S2, R)))) = (Q\Rightarrow ((e\Rightarrow wp(S1, R))\land (!e\Rightarrow wp(S2, R)))) = (Q\Rightarrow wp(\Cmd{if (e) S1; else S2;}, R))$

Циклы в терминах wp

В терминах слабейшего предусловия можно определить все оставшиеся еще неопределенными конструкции языка, но мы ограничимся только определением цикла while. Дело в том, что уже даже это определение оказывается достаточно бесполезным с точки зрения практики. Именно оно, однако, позволяет предложить несколько вполне конструктивных подходов к построению цикла, которые будут изучаться в следующей главе.

Для определения слабейшего предусловия wp("while(e)S;", R) нам потребуются следующие вспомогательные определения:

Определение 6.12. $H_0(R) = domain(e) \lands (!e \land R)$ , $H_k(R) = H_{k-1}(R) \lor (domain(e) \lands wp(S, H_{k-1}(R)))$ , где предикат H_k(R) описывает множество всех состояний, в которых выполнение цикла "while(e)S;" заканчивается не более, чем за итераций, в состоянии, удовлетворяющем .

Теперь можно дать основное определение.

Определение 6.13. 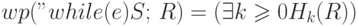$wp("while(e)S;", R) = (\exists k \geqslant 0 H_k(R))$ .

Для цикла "while (i<1) i=i+1;" и постусловия R=(i=1) имеем $H_0(R)= (i\geqslant1 \land i=1) = (i=1)$ . Действительно, именно при таком предусловии выполнение цикла завершится за ноль итераций и даст результат .

Далее, легко посчитать wp("i=i+1;",H_0(R))=
(i+1=1) = (i=0) и $H_1(R) = (i=1)\lor(i<1 \land i=0) = (i=1 \lor i=0)$ .

Аналогично находим $H_2(R)= (i=1 \lor i=0 \lor i=-1)$ и т.д.

Дальше >>

Авторизоваться

Основы информатики и программирования

Спецификация программ и преобразователь предикатов

Определение простейших операторов языка Java

Оператор if и слабейшее предусловие

Циклы в терминах wp

Вопросы и ответы